Author: Bernard Bel

Posted on

Bol Processor grammars

James Kippen & Bernard Bel

In Mira Balaban, Otto Laske et Kemal Ebcioglu (eds.) Understanding Music with AI, American Association for Artificial Intelligence Press, Menlo Park CA (1992): 366-400.

Abstract

Bol Processor gram­mars are an exten­sion of unre­strict­ed gen­er­a­tive gram­mars allow­ing a sim­ple rep­re­sen­ta­tion of string "pat­terns", here tak­en to mean rep­e­ti­tions and homo­mor­phic trans­for­ma­tions. These have been suc­cess­ful­ly applied to the sim­u­la­tion of impro­visato­ry tech­niques in tra­di­tion­al drum music, using a production-rule sys­tem called "Bol Processor BP1". The basic con­cepts and pars­ing tech­niques of BP1 are presented.

A new ver­sion of Bol Processor, name­ly "BP2", has been designed to serve as a aid to rule-based com­po­si­tion in con­tem­po­rary music. Extensions of the syn­tac­tic mod­el, such as metavari­ables, remote con­texts, sub­sti­tu­tions and pro­grammed gram­mars, are briefly introduced.

Excerpts of an AI review of this paper (Academia, June 2025)

Overview and Summary

The authors pro­pose a for­mal­ism, called "Bol Processor gram­mars," designed to cap­ture and sim­u­late per­for­mance and impro­visato­ry behav­iors in tra­di­tion­al drum music—particularly North Indian tabla. This work presents a detailed account of how their pro­posed grammar-based sys­tem (BP1 and sub­se­quent­ly BP2) man­ages musi­cal ele­ments such as gen­er­a­tive rules, pars­ing pro­ce­dures, and higher-order trans­for­ma­tions. The authors draw on con­cepts from for­mal lan­guage the­o­ry, specif­i­cal­ly incor­po­rat­ing string rewrit­ing, gen­er­a­tive gram­mars of vary­ing types (from context-free to unre­strict­ed), and pat­tern languages.

The mono­graph not only dis­cuss­es the­o­ret­i­cal frame­works but also pro­vides imple­men­ta­tions and exam­ples rel­e­vant to com­po­si­tion, impro­vi­sa­tion, and eth­no­mu­si­co­log­i­cal analy­sis. By com­bin­ing stan­dard gram­mars with addi­tion­al fea­tures (e.g., pat­tern rules, neg­a­tive con­texts, remote con­texts, sub­sti­tu­tions, homo­mor­phisms, and a sophis­ti­cat­ed weight­ing mech­a­nism), the Bol Processor aims to mod­el cre­ative aspects of impro­visato­ry traditions.

Contribution and Significance

  • The paper bridges the­o­ret­i­cal com­put­er sci­ence (rewrit­ing sys­tems, gen­er­a­tive gram­mars) with eth­no­mu­si­co­log­i­cal inquiry. This inter­dis­ci­pli­nary approach shows how lan­guage mod­els can adapt to musi­cal per­for­mance tra­di­tions, espe­cial­ly where oral trans­mis­sion prevails.
  • The authors intro­duce exten­sions to clas­si­cal Chomsky hier­ar­chies by incor­po­rat­ing string pat­tern lan­guages and homo­mor­phisms specif­i­cal­ly tai­lored for music com­po­si­tion and analy­sis. This advance­ment is espe­cial­ly valu­able to those research­ing com­pu­ta­tion­al musi­col­o­gy or algo­rith­mic composition.
  • By pro­vid­ing prac­ti­cal imple­men­ta­tion details and guide­lines (e.g., sub­gram­mars, weight­ing rules, context-sensitive sub­sti­tu­tions), the study con­veys a clear path for oth­ers look­ing to mod­el or sim­u­late impro­vi­sa­tion­al processes.

Strengths

  • Clarity of Theoretical Underpinnings: The text care­ful­ly explains the fun­da­men­tals of gen­er­a­tive gram­mars and pat­tern lan­guages, ensur­ing that read­ers unfa­mil­iar with for­mal lan­guage the­o­ry can still fol­low the ratio­nale behind the Bol Processor model.
  • Comprehensive Examples: The inclu­sion of worked-through gram­mar list­ings, detailed pars­ing traces, and real-world musi­cal seg­ments high­lights an applied per­spec­tive. Readers can see exact­ly how the rules oper­ate on con­crete musi­cal materials.
  • Interdisciplinary Integration: The man­u­script thought­ful­ly weaves togeth­er com­pu­ta­tion­al lin­guis­tics, eth­no­mu­si­col­o­gy, and com­po­si­tion, offer­ing a unique per­spec­tive to each discipline.
  • Generative and Analytical Capacities: Emphasizing both the gen­er­a­tion of new musi­cal vari­a­tions and the pars­ing of exist­ing per­for­mances demon­strates the system’s two-fold util­i­ty: it sup­ports cre­ative com­po­si­tion while pro­vid­ing a frame­work for empir­i­cal analysis.

Areas for Further Development

  • Handling of Larger-Scale Form: While the paper address­es theme-variation struc­tures, the method­ol­o­gy could be extend­ed to more exten­sive glob­al forms or multi-sectional pieces. More elab­o­ra­tion on how the gram­mar might man­age nest­ed forms or very long struc­tures would strength­en the approach.
  • Quantitative Evaluation: The text pro­vides evi­dence of suc­cess­ful mod­el­ing but could ben­e­fit from addi­tion­al dis­cus­sion of how cor­rect­ness or “musi­cal plau­si­bil­i­ty” is sys­tem­at­i­cal­ly test­ed, beyond anec­do­tal or inter­ac­tive ses­sions with experts.
  • Comparisons with Other Systems: A more in-depth com­par­i­son with exist­ing com­pu­ta­tion­al music sys­tems that also employ gen­er­a­tive gram­mars (e.g., pure­ly context-free or Markov-based approach­es) might deep­en an under­stand­ing of the Bol Processor’s unique contributions.

Readability and Presentation

  • The writ­ing is clear and con­sis­tent­ly struc­tured, espe­cial­ly around the dis­crete sec­tions (intro­duc­tion, pat­tern rules, pars­ing, and advanced fea­tures in BP2). Diagrams and gram­mar list­ings are help­ful, though fur­ther clar­i­fy­ing anno­ta­tions in some fig­ures could assist read­ers less famil­iar with for­mal notation.
  • The appen­dices excel in pre­sent­ing extend­ed exam­ples and step-by-step pars­es, adding trans­paren­cy to the meth­ods. This style of pre­sen­ta­tion ensures repro­ducibil­i­ty and offers insights into how to adapt or mod­i­fy the sys­tem for oth­er musi­cal styles.

Potential Impact on the Field

The sys­tem has appar­ent impli­ca­tions not just for tabla and oth­er per­cus­sion tra­di­tions but for any domain where com­plex vari­a­tions can be expressed in a rule-based man­ner. Likewise, com­posers work­ing with algo­rith­mic or computer-aided com­po­si­tion may dis­cov­er a robust set of tech­niques for shap­ing vari­a­tion, tex­ture, and form. Researchers in eth­no­mu­si­col­o­gy might find new ana­lyt­i­cal tools for uncov­er­ing sys­tem­at­ic ele­ments in impro­vi­sa­tion­al practices.

Overall, the work stands as a thor­ough explo­ration of gen­er­a­tive and pars­ing approach­es tai­lored to music, illus­trat­ing how com­pu­ta­tion­al mod­els can deep­en under­stand­ing of both fixed and impro­vised musi­cal structures.

Download this paper

View Fullscreen
Skip to PDF content

Posted on

The identification and modelling of a percussion ‘language’

James Kippen & Bernard Bel

Computers and the Humanities (1989), 23, 3: 119-214

Abstract

In exper­i­men­tal research into per­cus­sion ‘lan­guages', an inter­ac­tive com­put­er sys­tem, the Bol Processor, has been devel­oped by the authors to analyse the per­for­mances of expert musi­cians and gen­er­ate its own musi­cal items that were assessed for qual­i­ty and accu­ra­cy by the infor­mants. The prob­lem of trans­fer­ring knowl­edge from a human expert to a machine in this con­text is the focus of this paper. A pro­to­typ­i­cal gram­mat­i­cal infer­encer named QAVAID (Question Answer Validated Analytical Inference Device, an acronym also mean­ing ‘gram­mar' in Arabic/Urdu) is described and its oper­a­tion in a real exper­i­men­tal sit­u­a­tion is demon­strat­ed. The paper con­cludes on the nature of the knowl­edge acquired and the scope and lim­i­ta­tions of a cognitive-computational approach to music.

Excerpts of an AI review of this paper (Academia, June 2025)

Summary

This paper explores a nov­el approach to mod­el­ing North Indian tabla drum­ming as a “per­cus­sion lan­guage” by apply­ing for­mal lan­guage the­o­ry, machine learn­ing, and inter­ac­tive generative/analytic com­put­er meth­ods. The authors dis­cuss two sys­tems— Bol Processor and QAVAID — that each plays a dis­tinct role in ana­lyz­ing and gen­er­at­ing rhyth­mic pat­terns (termed “sen­tences”) under the guid­ance of expert infor­mants. They exam­ine how knowl­edge is incre­men­tal­ly acquired and for­mal­ized as a gram­mar, how alter­na­tive seg­men­ta­tions can be eval­u­at­ed, and how prob­a­bilis­tic mod­el­ing may be employed to gen­er­ate orig­i­nal musi­cal sen­tences for expert eval­u­a­tion. The work’s eth­no­mu­si­co­log­i­cal per­spec­tive unites com­pu­ta­tion­al for­mal­iza­tion with the real-world prac­tice of tabla impro­vi­sa­tion and teach­ing, rais­ing broad­er ques­tions about the nature of knowl­edge trans­fer between human expert, machine learn­er, and cul­tur­al context.

Contribution and Strengths

Interdisciplinary Framework

The paper posi­tions itself at the inter­sec­tion of musi­col­o­gy, cog­ni­tive sci­ence, com­pu­ta­tion­al lin­guis­tics, and ethnog­ra­phy. This breadth under­scores the com­plex­i­ty of “music as lan­guage” and effec­tive­ly high­lights the idea that music may be for­mal­ly scru­ti­nized with meth­ods akin to those in com­put­er science.

Formal Language Techniques

By ground­ing the analy­sis in the Chomskian hier­ar­chy (reg­u­lar and context-free gram­mars) and ref­er­enc­ing Gold’s con­cept of “iden­ti­fi­ca­tion in the lim­it,” the authors tie their eth­no­mu­si­co­log­i­cal obser­va­tions to well-established the­o­ret­i­cal under­pin­nings. These con­nec­tions help clar­i­fy why a sys­tem­at­ic, incre­men­tal approach to gram­mar infer­ence is suit­able for mod­el­ing the impro­vi­sa­tion­al com­po­nents of North Indian tabla drumming.

Attention to Vocabulary and Segmentation

The dis­cus­sion on how the sys­tem learns seg­men­ta­tion and defines “words” in the drum­ming lex­i­con is illu­mi­nat­ing. Though seg­ment­ing tabla phras­es is not anal­o­gous to seg­ment­ing words in spo­ken lan­guages, the authors show how incre­men­tal analy­sis can pro­pose, refine, or dis­card poten­tial lex­i­cal bound­aries in a prin­ci­pled manner.

Interactive and Incremental Learning

A sig­nif­i­cant fea­ture is the inter­ac­tive mod­el: the sys­tem gen­er­ates out­put strings that are val­i­dat­ed or reject­ed by the human infor­mant, there­by trig­ger­ing incre­men­tal adjust­ments to the gram­mar. This mim­ics student-teacher inter­ac­tions and demon­strates a strong attempt to reflect authen­tic learn­ing and teach­ing processes.

Probabilistic Aspect

Introducing sto­chas­tic­i­ty in syn­the­sis breaks from pure­ly deter­min­is­tic meth­ods. It points to a more real­is­tic reflec­tion of the ways in which live per­for­mance might involve cre­ative, non-deterministic choic­es, while main­tain­ing con­straints guid­ed by the learned grammar.

Methodological Observations

Data Representation

The authors clear­ly define the sym­bol inven­to­ry (bols like dha, ge, ti, etc.) and acknowl­edge the com­plex­i­ty of how these sym­bols relate to son­ic events. By lim­it­ing the approach to frequency-based seg­men­ta­tion and gram­mar infer­ence, the sys­tem oper­at­ing with­in a “text pre­sen­ta­tion pro­to­col” remains suit­ably rigorous.

User–System Dialogue

Illustrations of the QAVAID question–answer mech­a­nism high­light prac­ti­cal aspects of gram­mar con­struc­tion. This is valu­able for explain­ing how the sys­tem backs up, mod­i­fies rules, or infers new chunks based on par­tial dis­agree­ments from the expert and how it tests repeat­ed merges or seg­men­ta­tions for consistency.

Scalability Considerations

The exper­i­ments pre­sent­ed involve a lim­it­ed num­ber of exam­ples. The authors note com­pu­ta­tion­al con­straints and care­ful­ly frame how repeat­ed merges, lex­i­cal expan­sions, and neg­a­tive exam­ples (machine out­puts the user rejects) unfold in real­is­tic time on a micro­com­put­er. This trans­paren­cy about per­for­mance con­sid­er­a­tions is commendable.

Comparison to Existing Tools

While the authors ref­er­ence for­mal lan­guage the­o­ry, it could be help­ful to sit­u­ate the QAVAID approach more explic­it­ly along­side oth­er grammar-inference sys­tems (or music cog­ni­tion mod­els) in terms of effi­cien­cy and suc­cess rates. This might pro­vide addi­tion­al con­text about how QAVAID’s tight-fit method­ol­o­gy dif­fers from exist­ing machine-learning strate­gies in music.

Suggestions for Future Work

Integration of Connectionist Approaches

A deep­er inves­ti­ga­tion into how sub-symbolic learn­ing algo­rithms (e.g., neur­al net­works) might coex­ist or com­ple­ment a sym­bol­ic grammar-inference approach could shed light on whether deep­er hier­ar­chi­cal or pattern-based musi­cal struc­tures can be dis­cov­ered automatically.

Temporal and Metric Awareness

Incorporating real-time con­straints, includ­ing an explic­it mod­el of cycle bound­aries and tem­po vari­a­tions, might enable QAVAID or a suc­ces­sor sys­tem to han­dle per­for­mances that devi­ate sub­tly from rig­or­ous­ly mea­sured durations.

Generative Evaluation

Extending the sys­tem to pro­duce longer per­for­mance sequences and eval­u­at­ing how coher­ent or context-appropriate they sound in extend­ed impro­vi­sa­tion might reveal new facets of pat­tern syn­er­gy that short exam­ples do not expose.

Cross-Cultural Applicability

The strate­gies deployed here for tabla might prove adapt­able to oth­er deeply mnemon­ic or impro­visato­ry musi­cal tra­di­tions (e.g., West African drum­ming, Middle Eastern per­cus­sion). Investigating how the mod­el gen­er­al­izes across cul­tures could under­score the method’s ver­sa­til­i­ty and reveal new limitations.

Conclusion

By merg­ing for­mal lan­guage the­o­ry with eth­no­mu­si­co­log­i­cal field­work and machine learn­ing, the authors pro­pose a pow­er­ful mod­el for cap­tur­ing core aspects of tabla impro­vi­sa­tion. The frame­work encour­ages close human–computer col­lab­o­ra­tion through dynam­ic ques­tion­ing and incre­men­tal gram­mar build­ing. This approach not only advances a cognitive-computational per­spec­tive on music but also opens a path­way for fur­ther inquiries into cross-cultural appli­ca­tions, time-sensitive per­for­mance mod­el­ing, and cre­ative com­po­si­tion with­in implic­it musi­cal grammars.

Download this paper

View Fullscreen
Skip to PDF content

Posted on

Time and musical structures

Bernard Bel

Time and Musical Structures. Interface, 19 (2-3): 107-135.

Abstract

A the­o­ret­i­cal mod­el is intro­duced, by the aid of which descrip­tions of sequen­tial and con­cur­rent process­es may be built tak­ing account of the sophis­ti­ca­tion and gen­er­al­i­ty of con­tem­po­rary musi­cal con­cepts. This is achieved through an inde­pen­dent and unre­strict­ed map­ping between phys­i­cal time and a sym­bol­ic set of dates. Sequential struc­tures are con­sid­ered first, then the nature of this map­ping and its prac­ti­cle imple­men­ta­tion in a real-time syn­the­siz­er are dis­cussed. Polymetric struc­tures are intro­duced and a method is out­lined for map­ping events to sym­bol­ic dates when con­cur­rent process­es are incom­plete­ly described.

Excerpts of an AI review of this paper (Academia, June 2025)

Overview

This man­u­script explores a the­o­ret­i­cal frame­work for rep­re­sent­ing musi­cal time in both sequen­tial and con­cur­rent process­es. By map­ping phys­i­cal time onto sym­bol­ic dates, the work pro­vides a gen­er­al approach for deal­ing with com­plex musi­cal con­cepts such as poly­met­ric struc­tures, con­cur­ren­cy, and sym­bol­ic dura­tions. The study incor­po­rates ref­er­ences to pri­or research on for­mal music mod­el­ing, con­cur­ren­cy the­o­ry, automa­ta, and the notion of sieves (in the sense intro­duced by Xenakis). Overall, it offers a sys­tem­at­ic per­spec­tive on how time rep­re­sen­ta­tion can be divorced from strict phys­i­cal dura­tions, allow­ing com­po­si­tion­al and ana­lyt­i­cal mod­els to oper­ate at a more abstract level.

Strengths

Conceptual Clarity: The author artic­u­lates the dis­tinc­tion between phys­i­cal time and sym­bol­ic time con­vinc­ing­ly. This two-tiered approach — struc­ture of time ver­sus in-time struc­tures — makes the dis­cus­sion trans­par­ent and applic­a­ble to a wide array of musi­cal contexts.

Breadth of Coverage: The work address­es not only sequen­tial but also con­cur­rent process­es. The sec­tions on poly­met­ric struc­tures demon­strate that this mod­el can han­dle over­lap­ping and simul­ta­ne­ous events with­out los­ing consistency.

Technical Rigor: The paper’s for­mal descrip­tions — par­tic­u­lar­ly in Sections 7 and 9 — are thor­ough and pre­cise. The def­i­n­i­tions and func­tions (e.g., map­pings θ, φ, or the equiv­a­lence class­es for frac­tion­al time) demon­strate a strong math­e­mat­i­cal foundation.

Practical Implementations: References to real-time syn­the­siz­ers (e.g., SYTER), and exam­ples of how sym­bol­ic time can be con­vert­ed back to phys­i­cal time, high­light prag­mat­ic con­sid­er­a­tions. The man­u­script shows how these the­o­ret­i­cal insights can be imple­ment­ed in actu­al music soft­ware (HyperBP, MIDI inte­gra­tion, etc.).

Well-Selected References: The author con­nects their work to estab­lished the­o­ries (Boulez, Xenakis) and more con­tem­po­rary AI-related approach­es (Mazurkiewicz, Chemillier). This posi­tions the study with­in a lin­eage of rel­e­vant ideas, sup­port­ing both the nov­el­ty and valid­i­ty of the research.

Clarity and Organization

The paper is clear­ly writ­ten and sys­tem­at­i­cal­ly orga­nized. Definitions are intro­duced in a log­i­cal sequence, and the illus­tra­tive exam­ples — even though dense — pro­vide con­crete appli­ca­tions of the for­mal­ism. Some sec­tions (such as 7.1–7.2 and 9) might ben­e­fit from addi­tion­al exam­ples to ensure that read­ers not ful­ly immersed in for­mal math­e­mat­ics can fol­low the trans­for­ma­tions step by step.

Significance of the Work

By bridg­ing abstract math­e­mat­i­cal for­malisms and com­put­er imple­men­ta­tion details, the man­u­script offers a valu­able method­ol­o­gy for musi­cians, com­posers, musi­col­o­gists, and AI researchers. It can inform broad­er dis­cus­sions on how to han­dle simul­ta­ne­ous events, phrase-bound time manip­u­la­tions, and adap­tive tem­po set­tings with­in algo­rith­mic com­po­si­tion and music per­for­mance systems.

Conclusion

This study presents a thor­ough and care­ful­ly rea­soned frame­work for sym­bol­ic time rep­re­sen­ta­tion and manip­u­la­tion in music. It demon­strates clear poten­tial and is sit­u­at­ed well in the con­tin­u­um of exist­ing for­mal approach­es to musi­cal time. With addi­tion­al real-world usage exam­ples and deep­er com­par­isons to estab­lished con­cur­rent process par­a­digms, the man­u­script could become even more impact­ful. The core con­tri­bu­tion — name­ly, an adapt­able, polymetric-capable time rep­re­sen­ta­tion — address­es a fun­da­men­tal issue in con­tem­po­rary music com­put­ing, paving the way for inno­v­a­tive appli­ca­tions in both com­po­si­tion­al and per­for­mance systems.

Download this paper

View Fullscreen
Skip to PDF content
Posted on

Live coding

Live cod­ing is a per­form­ing art form cen­tred on writ­ing code and using inter­ac­tive pro­gram­ming in an impro­vi­sa­tion­al way. From March 2025, this prac­tice is pos­si­ble on all Bol Processor imple­men­ta­tions: MacOS, Windows, Linux and the stand­alone appli­ca­tion on Mac.

Practically speak­ing, live cod­ing on the Bol Processor is pos­si­ble when impro­vis­ing con­tin­u­ous­ly in real time MIDI. The project is a gram­mar, and the fol­low­ing real-time changes are cur­rent­ly possible:

  • Edit and save the gram­mar. The updat­ed ver­sion will be imme­di­ate­ly reloaded and restarted.
  • Edit and save the set­tings. The updat­ed ver­sion will be imme­di­ate­ly reloaded and applied to the next productions.
  • Save anoth­er gram­mar in the same ses­sion. It will be loaded imme­di­ate­ly to replace the cur­rent one and pro­duc­tion will restart. The set­tings (and alpha­bet, if applic­a­ble) will be included.

How to do it

  • Set the gram­mar in Non-stop improvize mode.
  • Check the Follow grammar(s) and (option­al) Follow set­tings options at the bot­tom of the set­tings form. The Track changes option will keep a record of gram­mar and set­tings changes.
  • Do the same for all gram­mars used in the improvisation.
  • Click PRODUCE ITEM(s) on the first grammar.
  • During the per­for­mance, click­ing SAVE on any of the gram­mars will save its changes, load it and run it in place of the cur­rent one. Its set­tings and alpha­bet will also be auto­mat­i­cal­ly included.

All the fea­tures of a real-time MIDI per­for­mance remain avail­able: micro­ton­al adjust­ments, parts, MIDI input cap­ture, wait instruc­tions, etc.

Example

The fol­low­ing is a triv­ial exam­ple with no musi­cal rel­e­vance. It is intend­ed to test the Bol Processor's tech­ni­cal abil­i­ty to quick­ly han­dle changes in a con­ver­sa­tion­al setup.

Two gram­mars, name­ly "-gr.livecode1" and "-gr.livecode2", con­tain a sin­gle infer­ence from S to a poly­met­ric expression:

-se.livecode1
S --> {_vel(64) _chan(1){4,{D6 A4 A4{1/2,G5 Bb5}{1/2,D6 C6 Bb5}, 1{Cb4,Eb4,F4,Ab4}{Bb3,D4,Gb4}-}},_vel(64) _chan(2){4,{D4 F3 E3{1/2,G3 Bb3}{1/2,D4 C4 Bb3}, 1{Db2,Ab2}{C2,G2}-}}}

-se.livecode2
S --> {_tempo(41/30) _vel(64) _chan(3){1319/240,{re4{17/120,fa1 fa2}17/1920{119/1920,la2}{17/80,do3 re3 fa3}103/40, 57/40{17/240,la3}601/240, 359/240 4, 359/240{17/120,do4 re4}17/1920{119/1920,fa4}{17/80,la4 do5 re5}499/240, 461/240{17/240,fa5}reb5{1,la3 sol#3}1/120, 479/120 1/120,{re3,sol3,la3}--{1,- fa3}}},_vel(64) _chan(4){4,{la2 -{1,- la0}reb3,{sib1,fa2}2{sol2,la2}}}}

In "-se.livecode1" and "-se.livecode2", the Non-stop improvize and Follow grammar(s) options have been checked.

First run "-gr.livecode1" which is a plain rep­e­ti­tion of a musi­cal motif bor­rowed from Oscar Peterson. Click SAVE to check that it restarts the per­for­mance. Then mod­i­fy the gram­mar, adding or delet­ing notes, and click SAVE to check that the mod­i­fied ver­sion will be played immediately.

If the Follow set­tings option is checked, you will notice that chang­ing a set­ting, such as tem­po, and click­ing SAVE to “-se.livecode1” will be reflect­ed in the per­for­mance. However, the effect is not imme­di­ate, as the machine must first play the items stored in the out­put buffer. We're work­ing on a way to make changes imme­di­ate while main­tain­ing the con­ti­nu­ity of the performance.

Listen to a pos­si­ble result (!):

Grammars "-gr.livecode1" and "-gr.livecode2" in a 'con­ver­sa­tion­al" mode

It is worth not­ing that the two gram­mars use dif­fer­ent note con­ven­tions, name­ly English in "-gr.livecode1" and Italian/French in "-gr.livecode2".

A more complex example

Let us now mix two com­plex gram­mars: "-gr.Mozart" and "-gr.trial.mohanam", which are in the "ctests" fold­er. Check the Non-stop improvize and Follow grammar(s) options in their set­tings and start impro­vis­ing on one of them. Then click SAVE to change the gram­mar or reload the cur­rent one.

In fact, you can use more than two gram­mars for this exer­cise. You can also include a gram­mar that is not in the Non-stop improvize mode, so it will end the performance.

The "-gr.Mozart" gram­mar uses the French note con­ven­tion where­as the "-gr.trial.mohanam" gram­mar uses the Indian con­ven­tion. The lat­ter also uses an alpha­bet file "-al.trial.mohanam". The merge is tech­ni­cal­ly sat­is­fac­to­ry as you can hear:

Work in progress

We're work­ing on three lim­i­ta­tions that seem evi­dent in the con­text of live coding:

  1. React imme­di­ate­ly to changes in the settings.
  2. Create an option to react to changes (or updates) of a gram­mar only at the moment when an entire ele­ment has been sent to MIDI.
  3. When load­ing a gram­mar, if the gram­mar is not valid, the impro­vi­sa­tion should con­tin­ue with the pre­vi­ous grammar.

More sug­ges­tions are sure to come as feed­back from artists work­ing with live cod­ing. These will give way to chal­leng­ing developments!

Posted on

Move data

In the stan­dard use of the Bol Processor, all data is stored in the "htdocs/bolprocessor" fold­er cre­at­ed by MAMP or XAMPP, or "Contents/Resources/www" with the stand­alone "BolProcessor.app" appli­ca­tion on MacOS. Read the instal­la­tion instruc­tions for more details.

This pack­ag­ing is accept­able in most cas­es because Bol Processor data is basi­cal­ly made of text files that do not take up much space.

However, there are a num­ber of rea­sons why a user might want to store data in loca­tions oth­er than this folder:

  1. Need for addi­tion­al space
  2. Avoid stor­ing data on the start­up disk
  3. Sharing data with oth­er appli­ca­tions and oth­er users
  4. Sharing data via a cloud device (e.g. DropBox).

A pro­ce­dure for mov­ing the entire "bolprocessor" fold­er is described in the instal­la­tion instruc­tions: for exam­ple, in the MacOS envi­ron­ment. Unfortunately, as of today, the relo­cat­ed instal­la­tion does not work on MacOS with XAMPP after a reboot, unless the "BolProcessorInstaller.pkg" installer is run again. The same prob­lem might exist in both Windows and Linux envi­ron­ments where MAMP or XAMPP is used.

In fact, there is not much inter­est in relo­cat­ing the entire "bolprocessor" (or "Contents/Resources/www") fold­er. Moving data fold­ers out­side this fold­er will suf­fice. This tuto­r­i­al will tell you how to do this.

The first time you install the Bol Processor, the "bolprocessor" (or "Contents/Resources/www") fold­er con­tains a unique fold­er called "ctests" for stor­ing data. This fold­er con­tains exam­ples that are updat­ed when a new ver­sion is installed. However, you can use it to store new projects, new sub­fold­ers, etc., which will not be affect­ed by new versions.

You can also cre­ate your own fold­ers (and sub­fold­ers) at the same lev­el as "ctests". The inter­face is designed for the cre­ation, mov­ing and dele­tion of fold­ers and files with­in the "bolprocessor" (or "Contents/Resources/www") fold­er. Always use the inter­face. Creating a fold­er (or a file) via the Finder or File Manager may not work, espe­cial­ly if the Bol Processor is run with XAMPP, because the own­er may be dif­fer­ent from the Apache server's iden­ti­ty. For geeks: XAMPP runs as "dae­mon" while the Finder runs as your per­son­al identity.

Creating fold­ers and files with­out using the Bol Processor inter­face may result in "per­mis­sion errors" when a file is saved. Indeed, there are workarounds, for those famil­iar with shell scripts, for exam­ple the "change_permissions.sh" script designed for Linux and MacOS. But this is not a pleas­ant way to use the Bol Processor…

In short, always cre­ate fold­ers using the CREATE FOLDERS func­tion in the inter­face. Once cre­at­ed, they can be moved (even with the Finder or File Manager) with­in the "bolprocessor" fold­er, and even renamed. The Bol Processor will always recog­nise them as its own.

Below is an exam­ple of two fold­ers called "data" and "my_data" cre­at­ed at the same lev­el as "ctests":

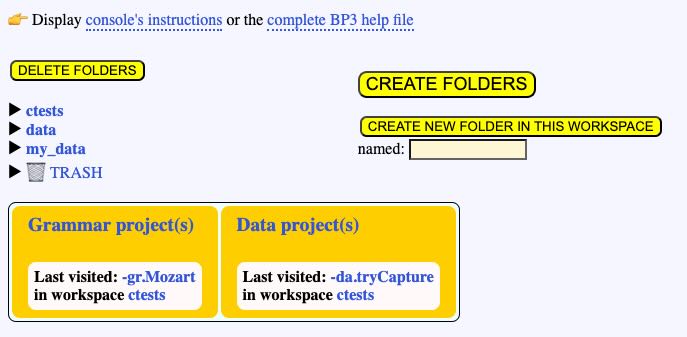
Now, how can we move a fold­er out­side the "bolprocessor" (or "Contents/Resources/www") fold­er? Once we've moved it, the inter­face no longer shows it. For exam­ple, let us do this with "my_data". (The fold­er may be emp­ty or con­tain oth­er fold­ers and files.)

Using the Finder in MacOS, or copy/paste in Windows and Linux, we move "my_data" to the desired loca­tion, for exam­ple a "MUSIC" fold­er at the root of an exter­nal dri­ve called "EXT". Make sure that this loca­tion accepts read/write operations.

At this point, there is no more "my_data" in "bolprocessor" (or "Contents/Resources/www"), or we delete it using the DELETE FOLDERS but­ton. You can't delete "ctests" with this delete function.

To make "my_data" vis­i­ble again from its remote loca­tion, we need to cre­ate a sym­bol­ic link. Unfortunately, the Bol Processor's inter­face can­not do this due to secu­ri­ty restric­tions. I've spent hours with a chat­bot try­ing to find a workaround!

In MacOS and Linux, the sym­bol­ic link is cre­at­ed from a (Unix) Terminal. In Windows, you will use the Windows PowerShell (admin).

This pro­ce­dure doesn't work with alias­es cre­at­ed by the Finder in MacOS. You real­ly need to use sym­bol­ic links.

MacOS or Linux

Open the Terminal (in the Applications fold­er) and point it to the "htdocs/olprocessor" (or "Contents/Resources/www") direc­to­ry. For those unfa­mil­iar with Unix com­mands, you will need to type "cd " (fol­lowed by a space) and drag "bolprocessor" (or "www") to the end of this com­mand, then press "return". You can type the instruc­tion "ls -al" to see the con­tents of "bolprocessor" (or "www"), which con­tains "ctests", and more.

Suppose that your "MUSIC" fold­er is on disk "EXT" and you want to link to the relo­cat­ed "my_data" fold­er. Type this command:

ln -s /Volumes/EXT/MUSIC/my_data my_data

This will cre­ate the "my_data" sym­bol­ic link point­ing to the remote "my_data" fold­er. Check that the link has been cre­at­ed by typ­ing "ls -al".

Depending on the disk or disk area used to store relo­cat­ed data, you might encounter prob­lems due to MacOS access restric­tions, espe­cial­ly if the System Integrity Protection (SIP) is enabled.

If you are using a recent installer (as of 3 Feb 2025) and a XAMPP Apache serv­er, the 'daemon' iden­ti­ty used by XAMPP is auto­mat­i­cal­ly added to the 'admin', 'wheel' and 'staff' groups which are com­mon­ly used by the Finder.

There are prob­a­bly few­er restric­tions with MAMP because this serv­er runs under your per­son­al iden­ti­ty, and file own­ers are set to that identity.

Windows

Right-click the start icon at the bot­tom left of the screen, and select Windows PowerShell (admin). Then type the fol­low­ing com­mand to cre­ate a sym­bol­ic link — in fact a junc­tion (/J instead of /D):

cmd /c mklink /J "C:\MAMP\htdocs\bolprocessor\my_data" "D:\MUSIC\my_data"

If you are using XAMPP, replace "\MAMP\" with "\xampp\".

Depending on the disk or disk area used to store relo­cat­ed data, you may encounter issues due to Windows 10 access restrictions.

For exam­ple, mov­ing your data to the OneDrive direc­to­ry won't work by default. If you must keep the tar­get fold­er inside OneDrive, you must dis­able the syn­chro­ni­sa­tion of your files:

  • Open OneDrive Settings
  • Go to "Choose fold­ers"
  • Uncheck your data folder(s).

Return to the Bol Processor

Now, the BolProcessor inter­face will show "my_data" as if the fold­er was in "bolprocessor". If it doesn't, make sure that the paths used to cre­ate the link were correct.

Make sure that you can cre­ate and save data in the relo­cat­ed fold­er. Welcome to shared projects!

Posted on

Control of NoteOn/NoteOff

   

This page is intend­ed for devel­op­ers of the Bol Processor BP3 (read instal­la­tion). It is not a for­mal descrip­tion of the algo­rithms car­ried by the console's C code, but rather an illus­tra­tion of their man­age­ment of musi­cal process­es, which may be use­ful for check­ing or extend­ing algorithms.

When the Bol Processor pro­duces MIDI mate­r­i­al (real-time or files), each note is asso­ci­at­ed with two events: a NoteOn at its begin­ning and a NoteOff at its end. Additional para­me­ters are its veloc­i­ty (range 0 to 127) and its MIDI chan­nel (range 1 to 16).

When a key­board instru­ment is used to pro­duce the sound, each NoteOn will press a key at the appro­pri­ate loca­tion. By default, note C4 (in English nota­tion) will press key #60. A NoteOff of the same pitch will release the key.

All exam­ples on this page can be found in the "-da.checkNoteOff" project. NoteOn/NoteOff track­ing can be enabled by select­ing this option in the "-se.checkNoteOff" set­tings of the project.

Read also: Csound check­up

Superimposed notes

Consider this example:

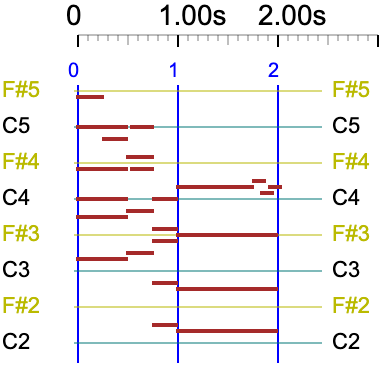
{C4____, -C4__-, --C4--} D4

Two (or more) con­sec­u­tive NoteOns of the same note and the same chan­nel should not be sent to a MIDI instru­ment. Nevertheless, the attacks of C4, which occur at the 1.00 s and 2.00 s times in this exam­ple, should be audi­ble. To achieve this, they are auto­mat­i­cal­ly pre­ced­ed by a NoteOff.

The list of NoteOn/NoteOff events is as follows:

NoteOn C4 chan­nel 1 at 0 ms
NoteOff C4 channel 1 at 1000 ms
NoteOn C4 chan­nel 1 at 1000 ms
NoteOff C4 channel 1 at 2000 ms
NoteOn C4 chan­nel 1 at 2000 ms
NoteOff C4 chan­nel 1 at 5000 ms
NoteOn D4 chan­nel 1 at 5000 ms
NoteOff D4 chan­nel 1 at 6000 ms

This fea­ture is not nec­es­sary for the cre­ation of Csound scores. The score gen­er­at­ed by this exam­ple is as follows:

i1 0.000 5.000 8.00 90.000 90.000 0.000 0.000 0.000 0.000 ; C4
i1 1.000 3.000 8.00 90.000 90.000 0.000 0.000 0.000 0.000 ; C4
i1 2.000 1.000 8.00 90.000 90.000 0.000 0.000 0.000 0.000 ; C4
i1 5.000 1.000 8.02 90.000 90.000 0.000 0.000 0.000 0.000 ; D4

Below we will show a refine­ment of this process for fast move­ments: read Dealing with fast move­ments.

NoteOn timing on fast movements

Let us look at this musi­cal phrase played with a metronome at 60 beats per second:

{3/2, {E5 A4 E5}, {{1/8, C#4 D4} {7/8, C#4} B3 C#4}}

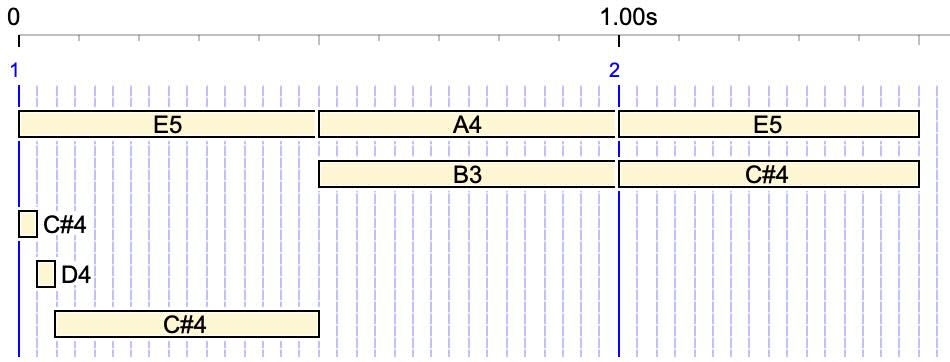
Excerpt of François Couperin "Le Petit Rien" (1722)

Fast move­ments could be prob­lem­at­ic when using a _rndtime(x) con­trol, which sends NoteOns at ran­dom times ± x mil­lisec­onds, for example:

_rndtime(50) {3/2, {{1/8, C#4 D4} {7/8, C#4} B3 C#4}}

A large ran­dom time (50 ms) has been cho­sen to make the graphs clear­er. In gen­er­al, _rndtime(x) is used for a less mechan­i­cal ren­der­ing of simul­ta­ne­ous notes, with 10 to 20 ms being the rec­om­mend­ed val­ue for key­board instruments.

Errors would occur if the order of fast notes were reversed. However, this does not hap­pen because the tim­ing of the NoteOns in fast move­ments is not made random:

The same excerpt with 50 ms ran­dom time, except on the start­ing fast sequence C#4 D4 C#4.

Below we will deal with the elim­i­na­tion of some NoteOns except in fast move­ments: read Dealing with fast move­ments.

The fol­low­ing exam­ple is the (slowed down) first mea­sure of François Couperin's Les Ombres Errantes (1730) (read page) with a quan­ti­za­tion of 50 ms and a ran­domi­sa­tion of 50 ms:

_tempo(1/2) _rndtime(50) {{3, _legato(20) C5 _legato(0){1/4,C5 B4 C5}{3/4,B4}_legato(20) Eb5,{1/2,Eb4}{5/2,G4 D4 F4 C4 Eb4},Eb4 D4 C4}}

First mea­sure of François Couperin's Les Ombres Errantes (1730) with quan­ti­za­tion and ran­domised NoteOns

These rel­a­tive­ly high val­ues have been cho­sen to show that the order of notes is respect­ed in fast move­ments. Quantization (typ­i­cal­ly 20 ms) is gen­er­al­ly nec­es­sary to play a com­pli­cat­ed poly­met­ric struc­ture, such as an entire piece of music. Once the times of the NoteOns have been cal­cu­lat­ed and round­ed to the quan­ti­za­tion grid, they are giv­en small ran­dom changes. However, notes in a fast motion (C5 B4 C5) and the first note after this motion (B4) are exclud­ed from the randomisation.

Duplication of notes in a MusicXML score

When sev­er­al MIDI chan­nels are used, we can imag­ine that each of them con­trols a sep­a­rate key­board, or that the chan­nels are com­bined to con­trol the same key­board. The first case is called Omni Off Poly mode and the sec­ond case is called Multi mode (see details).

Importing music from MusicXML scores often cre­ates a Bol Processor score that uses dif­fer­ent MIDI chan­nels (or Csound instru­ments). If the music is sent on a sin­gle chan­nel or played by an instru­ment in Multi mode, there may be over­laps for the same note assigned to dif­fer­ent channels.

This sit­u­a­tion is also found in music import­ed from MusicXML scores (see details of this process). For exam­ple, again the first mea­sure of François Couperin's Les Ombres errantes:

Original staff (source) - Creative Commons CC0 1.0 Universal
This (slowed down) inter­pre­ta­tion is micro­ton­al­ly adjust­ed accord­ing to the Rameau en si bémol tem­pera­ment (see expla­na­tion).

Notes at the bot­tom of the staff: Eb4, D4, C4 are shown both as quar­ter notes and as eight notes. As this dual sta­tus can­not be man­aged in the MusicXML score, they are dupli­cat­ed (link to the XML score). This dupli­ca­tion is nec­es­sary for the con­ven­tion­al rep­re­sen­ta­tion of the staff.

The staff would look less con­ven­tion­al if the redun­dant eight notes Eb4, D4, C4 were sup­pressed (link to the mod­i­fied XML score):

Modified staff drawn by MuseScore 3

The out­put of the Bol Processor from the orig­i­nal XML score is as fol­lows, with dupli­cate notes clear­ly marked:

A sound-object dis­play of the Bol Processor's inter­pre­ta­tion of the MusicXML score.
Note that the dura­tions of C5 and Eb5 are extend­ed to allow slurs to be played cor­rect­ly (see expla­na­tion)

The Bol Processor score is an over­lay of three lines cre­at­ed by sequen­tial­ly inter­pret­ing the XML score:

C5 slur {1/4,C5 B4 C5} {3/4,B4} Eb5 slur
{1/2,Eb4}{5/2,G4 D4 F4 C4 Eb4}
Eb4 D4 C4

which is then con­vert­ed into a sin­gle poly­met­ric expres­sion (with lega­to in place of slurs):

-to.tryTunings
_scale(rameau_en_sib,0) {3, _legato(20) C5 _legato(0) {1/4, C5 B4 C5} {3/4, B4} _legato(20) Eb5, {1/2, Eb4}{5/2, G4 D4 F4 C4 Eb4}, Eb4 D4 C4}

Eliminating the redun­dant eight notes Eb4, D4, C4 would require a back­track­ing to mod­i­fy the sec­ond line when read­ing the notes of the third line. But this com­pli­cat­ed process is not nec­es­sary because the Bol Processor han­dles dupli­cate notes cor­rect­ly. The fol­low­ing piano roll shows this:

A piano roll dis­play of the Bol Processor's inter­pre­ta­tion of the MusicXML score. 

This ren­der­ing requires a prop­er con­trol of NoteOffs and NoteOns. This can be done in sev­er­al ways. (For geeks) we present the old method (before ver­sion BP3.2) and the new one.

The old method

Events list­ed by the PianoTeq synthesiser

The image on the right shows the begin­ning of a sequence of MIDI events played by a syn­the­sis­er. (The date "6.802" is actu­al­ly time 0.) Events are dis­trib­uted on sep­a­rate MIDI chan­nels to allow for micro­ton­al adjust­ments by the pitch­ben­der. (Pitchbender mes­sages are not displayed.)

The per­for­mance starts with a NoteOn C5, then a NoteOn Eb4 at the same date. However, anoth­er NoteOn Eb4 is required at the same time. However, two NoteOns of the same note and the same chan­nel should not be sent to a MIDI instru­ment. so, a NoteOff Eb4 is sent just before the sec­ond NoteOn Eb4, all at the same time. In this way, the first NoteOn/NoteOff EB4 sequence is not audi­ble because its dura­tion is zero.

At time 1 sec­ond, a NoteOn C4 is sent as expect­ed. The sound-object graph shows that the Eb4 eight note is end­ing, but no NoteOff is sent because the Eb4 quar­ter note should con­tin­ue to sound. The NoteOff Eb4 will only occur at time 2 seconds.

The new method

In the old method, sequences of NoteOn and Noteoff of the same note could be sent to the syn­the­sis­er at the same time. This worked because the NoteOn/Noteoff order was respect­ed, and they could be processed by the syn­the­sis­er even if the times were (almost) iden­ti­cal. The new method aims to elim­i­nate this case.

To achieve this, the machine cal­cu­lates "MaxDeltaTime", an esti­mate of the max­i­mum time between two NoteOns (of the same note and chan­nel), beyond which they should be inter­pret­ed as sep­a­rate events. If dates are ran­domised by _rndtime(x), then MaxDeltaTime is set to 2 times x. Otherwise it is set to 2 times the quan­ti­za­tion. If there is no quan­ti­za­tion and no ran­domi­sa­tion, it is set to 20 milliseconds.

A Trace NoteOn/Noteoff option can be select­ed in the new ver­sion to dis­play the sequence of notes along with indi­ca­tions of deci­sions made to send or keep a NoteOn mes­sage. Here is the sequence for the first mea­sure of Couperin's Les Ombres Errantes ran­domised to ± 50 ms and quan­ti­fied to 20 ms. Therefore, we expect MaxDeltaTime to be set to 100 milliseconds.

_tempo(1/2) _rndtime(50) {{3, _legato(20) C5 _legato(0){1/4,C5 B4 C5}{3/4,B4}_legato(20) Eb5,{1/2,Eb4}{5/2,G4 D4 F4 C4 Eb4},Eb4 D4 C4}}

The NoteOn/NoteOff trace is as follows:

NoteOn Eb4 chan­nel 1 at 2 ms
NoteOn C5 chan­nel 1 at 14 ms
? Eb4 channel 1 at = 27 ms, last = 2, delta = 25 > 100 ms ¿
NoteOn G4 chan­nel 1 at 1031 ms
? C5 channel 1 at = 1955 ms, last = 14, delta = 1941 > 100 ms ¿
NoteOff C5 chan­nel 1 at 1955 ms
NoteOn C5 chan­nel 1 at 1955 ms
NoteOn D4 chan­nel 1 at 1995 ms
NoteOff Eb4 chan­nel 1 at 2002 ms
? D4 chan­nel 1 at = 2030 ms, last = 1995, delta = 35 > 100 ms ¿
NoteOff G4 chan­nel 1 at 2031 ms
NoteOn B4 chan­nel 1 at 2159 ms
? C5 channel 1 at = 2316 ms, last = 1955, delta = 361 > 100 ms ¿
NoteOff C5 chan­nel 1 at 2316 ms
NoteOn C5 chan­nel 1 at 2316 ms
NoteOff B4 chan­nel 1 at 2326 ms
NoteOff C5 chan­nel 1 at 2483 ms
NoteOn B4 chan­nel 1 at 2497 ms
NoteOn F4 chan­nel 1 at 2961 ms
NoteOn C4 chan­nel 1 at 3951 ms
NoteOff F4 chan­nel 1 at 3961 ms
NoteOff D4 chan­nel 1 at 3995 ms
NoteOff B4 chan­nel 1 at 3997 ms
NoteOn Eb5 chan­nel 1 at 4031 ms
? C4 chan­nel 1 at = 4040 ms, last = 3951, delta = 89 > 100 ms ¿
NoteOn Eb4 chan­nel 1 at 4981 ms
NoteOff C4 chan­nel 1 at 5951 ms
NoteOff Eb4 chan­nel 1 at 5981 ms
NoteOff Eb5 chan­nel 1 at 6431 ms

This trace shows that the machine com­pared the time inter­val between suc­ces­sive NoteOns of the same note and chan­nel. On the green line, this inter­val was 25 ms, which is less than 100 ms, so the Eb4 NoteOn (of the dupli­cat­ed note) was dis­card­ed. On the red lines, the inter­vals were greater than 100 ms and the NoteOns were played.

Channel infor­ma­tion is irrel­e­vant, as micro­ton­al adjust­ments assign a spe­cif­ic chan­nel to each note and its pitch­bend adjust­ment. However, this selec­tion of NoteOns is made pri­or to the assign­ment of spe­cif­ic chan­nels for micro­ton­al corrections.

Dealing with fast movements

The new method (BP3.2.0 and high­er) elim­i­nates NoteOns of the same note and chan­nel if they occur in an inter­val less than MaxDeltaTime. However it takes into account fast move­ments. For example:

_rndtime(50) {3/2, {E5 A4 E5}, {{1/8, C#4 D4} {7/8, C#4} B3 C#4}}

In this exam­ple, two dif­fer­ent occur­rences of C#4 should be sep­a­rat­ed by less than MaxDeltaTime (100 ms). The fol­low­ing trace shows that the sequence C#4 D4 C#4 (a trill) has been iden­ti­fied as a fast move­ment, and no time sep­a­ra­tion con­di­tion has been applied:

NoteOn C#4 chan­nel 1 at 0 ms
NoteOn E5 chan­nel 1 at 14 ms
NoteOff C#4 chan­nel 1 at 31 ms
NoteOn D4 chan­nel 1 at 31 ms
NoteOff D4 chan­nel 1 at 62 ms
NoteOn C#4 chan­nel 1 at 62 ms
NoteOn B3 chan­nel 1 at 493 ms
NoteOff C#4 chan­nel 1 at 500 ms
NoteOff E5 chan­nel 1 at 514 ms
NoteOn A4 chan­nel 1 at 531 ms
NoteOn E5 chan­nel 1 at 955 ms
NoteOn C#4 chan­nel 1 at 983 ms
NoteOff B3 chan­nel 1 at 993 ms
NoteOff A4 chan­nel 1 at 1031 ms
NoteOff E5 chan­nel 1 at 1455 ms
NoteOff C#4 chan­nel 1 at 1483 ms

A quan­ti­za­tion of 20 ms may not be desir­able for ren­der­ing fast move­ments such as:

{1/16, C4 - E4 F4} {15/16, G4 A4 B4}

The graph­ic shows that notes E4 and F4 have been assigned the same time (60 ms)

If the quan­ti­za­tion is set to 10 ms, the dif­fer­en­ti­a­tion of the tim­ings is retained:

NoteOn C4 chan­nel 1 at 0 ms
NoteOff C4 chan­nel 1 at 15 ms
NoteOn E4 chan­nel 1 at 31 ms
NoteOff E4 chan­nel 1 at 46 ms
NoteOn F4 chan­nel 1 at 46 ms
NoteOff F4 chan­nel 1 at 62 ms
NoteOn G4 chan­nel 1 at 62 ms
NoteOff G4 chan­nel 1 at 375 ms
NoteOn A4 chan­nel 1 at 375 ms
NoteOff A4 chan­nel 1 at 687 ms
NoteOn B4 chan­nel 1 at 687 ms
NoteOff B4 chan­nel 1 at 1000 ms

i1 0.000 0.015 8.00 90.000 90.000 0.000 0.000 0.000 0.000 ; C4
i1 0.031 0.015 8.04 90.000 90.000 0.000 0.000 0.000 0.000 ; E4
i1 0.046 0.016 8.05 90.000 90.000 0.000 0.000 0.000 0.000 ; F4
i1 0.062 0.313 8.07 90.000 90.000 0.000 0.000 0.000 0.000 ; G4
i1 0.375 0.312 8.09 90.000 90.000 0.000 0.000 0.000 0.000 ; A4
i1 0.687 0.313 8.11 90.000 90.000 0.000 0.000 0.000 0.000 ; B4

Created by Bernard Bel, January 2025

Posted on

Install the Bol Processor (BP3)

Installing the Bol Processor (BP3) does not require any pro­gram­ming skills. Just down­load and run the installers for MacOS and Windows, or the instal­la­tion scripts for Linux. The same installers and scripts can be used to upgrade an exist­ing BP3 with­out any loss of data or change to the settings.

On MacOS the pro­ce­dure is very sim­ple: run the installer to create/upgrade the stand­alone "BolProcessor.app" appli­ca­tion.

👉  You can also run the Bol Processor BP3 on MacOS with a HTML/PHP serv­er. Features are iden­ti­cal for both options.

 On Windows and Linux, you still need to install a local Apache HTML/PHP serv­er on your desk­top com­put­er. This serv­er runs a ded­i­cat­ed web ser­vice that is restrict­ed to your com­put­er. Only PHP (with its GD Graphics option) needs to be run­ning, as no data­base is used by the Bol Processor interface.

On MacOS and Windows we rec­om­mend MAMP or XAMPP, both of which are Apache servers with pre-installed fea­tures. On Linux, XAMPP is the only choice. This part of the imple­men­ta­tion is described on the pages that show the instal­la­tion of BP3 in the dif­fer­ent envi­ron­ments, see below.

Once you've installed MAMP or XAMPP, installing Bol Processor is almost a one-click process.

A help file will be com­piled when run­ning the Bol Processor. You can read a pre­view.

MacOS users can quick­ly do the instal­la­tion using a (nota­rized) installer called BolProcessorInstaller.pkg.
Follow instruc­tions on this page.

Windows users can quick­ly do the instal­la­tion using a (cer­ti­fied) installer called BolProcessorInstaller.exe.
Follow instruc­tions on this page.

Linux users can quick­ly do the instal­la­tion using ded­i­cat­ed scripts.
Follow instruc­tions on this page.

👉   Once you've installed the Bol Processor, vis­it this page to famil­iarise your­self with how to use it.

The file structure of your installation

👉  Only for geeks!

The fol­low­ing is the file struc­ture when run­ning the Bol proces­sor with an Apache HTML/PHP serv­er. If you have installed the stand­alone "BolProcessor.app" appli­ca­tion, the struc­ture is made vis­i­ble by select­ing "Show Package Contents" and mov­ing down to "Contents/Resources/www", which is spe­cif­ic to PHP Desktop.

Let us assume that your instal­la­tion was suc­cess­ful. It cre­at­ed a "htdocs/bolprocessor" fold­er.

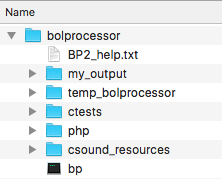
The file struc­ture inside this fold­er is shown on the left. There is noth­ing relat­ed to Bol Processor out­side of this folder.

This image includes "bp" which is the com­piled ver­sion of the BP3 con­sole for MacOS. The con­sole is called "bp.exe" in Windows and "bp3" in Linux. In Linux, "bp3" will not be vis­i­ble imme­di­ate­ly after the instal­la­tion because it needs to be cre­at­ed (in a sin­gle click) by the com­pil­er. In Windows, "bp.exe" is installed, so that no com­pi­la­tion is required. The same is true for "bp" in MacOS.

The "temp_bolprocessor" and "my_output" fold­ers are auto­mat­i­cal­ly cre­at­ed when the inter­face is run. The con­tents of the "temp_bolprocessor" fold­er is cleared of all files/folders old­er than 24 hours which were cre­at­ed in a dif­fer­ent session.

Another fold­er called "midi_resources" is also cre­at­ed to store the set­tings for your real-time MIDI input and out­put ports.

Two addi­tion­al fold­ers, "csound_resources" and "tonality_resources", are cre­at­ed by the instal­la­tion and filled with data shared by all projects.

Running the inter­face will also cre­ate "BP2_help.html" in the "php" fold­er using "BP2_help.txt" as its source.

The "ctests" fold­er — which we call a work­space — con­tains sam­ple mate­r­i­al used to check the oper­a­tion of Bol Processor and to illus­trate some musi­co­log­i­cal issues. It is updat­ed by the instal­la­tion scripts each time you upgrade to a new version.

If you cre­ate new mate­r­i­al in the "ctests" work­space it won't be delet­ed by upgrades. However, if you mod­i­fy files that come from the dis­tri­b­u­tion, they will revert to the cur­rent dis­tri­b­u­tion ver­sion on each upgrade. It is there­fore a good idea to keep a copy of the "ctests" fold­er, as you are like­ly to mod­i­fy some of its data files while using the pro­gram. You may want to restore the orig­i­nal ver­sions lat­er. You can also cre­ate your own work­spaces (in tree struc­tures) using your computer's file manager.

GitHub repositories

👉  Only for geeks!

Accessing GitHub repos­i­to­ries is not a reli­able method for installing or updat­ing the Bol Processor. The fol­low­ing infor­ma­tion is pro­vid­ed for ref­er­ence only. The files labelled "last ver­sion" are the ones down­loaded by the installer scripts.

Files for the Bol Processor project are stored in three repositories:

These con­tents may vary across devel­op­ments. Therefore, pri­or­i­ty should be giv­en to using installers or instal­la­tion scripts.

Posted on

Produce all items

 
The core of the Bol Processor, in all its ver­sions, is an infer­ence engine capa­ble of gen­er­at­ing  'items'  — strings of vari­ables and ter­mi­nal sym­bols — treat­ed like the score of a musi­cal work. The infer­ence engine does this through the use of rules from a for­mal grammar.

In its ini­tial ver­sions (BP1 and BP2), the infer­ence engine was also able to analyse a score — for exam­ple, a sequence of drum beats — to check its valid­i­ty against the cur­rent gram­mar. This fea­ture is not (yet) imple­ment­ed in BP3.

A brief presentation of grammars

The gram­mars used by the Bol proces­sor are sim­i­lar to those described in for­mal lan­guage the­o­ry with a com­pre­hen­sive layout:

  • Rules can be context-sensitive, includ­ing with remote con­texts on the left and the right.
  • Rules can con­tain pat­terns of exact or pseu­do rep­e­ti­tions of frag­ments. Pseudo rep­e­ti­tions make use of trans­for­ma­tions (homo­mor­phisms) on the ter­mi­nal symbols.
  • A ter­mi­nal sym­bol rep­re­sents a time object which can be instan­ti­at­ed as a sim­ple note or a sound object, i.e. a sequence of sim­ple actions (MIDI mes­sages or Csound score lines).
  • The gram­mars are lay­ered — we call them 'trans­for­ma­tion­al'. The infer­ence engine first does every­thing it can with the first gram­mar, then jumps to the sec­ond, and so on.

The “produce all items” procedure

Grammars can pro­duce infi­nite strings of sym­bols if they con­tain recur­sive rules. This is of no prac­ti­cal use in the  Bol Processor, as it will even­tu­al­ly lead to a mem­o­ry over­flow. When recur­sive rules are used, con­trol is exer­cised by dynam­i­cal­ly decreas­ing rule weights or using  'flags'  to inval­i­date recursivity.

This means that the machine only gen­er­ates finite lan­guages with­in its tech­ni­cal lim­i­ta­tions. Theoretically, it should be able to enu­mer­ate all pro­duc­tions. This is the aim of the "pro­duce all items" pro­ce­dure. In addi­tion, iden­ti­cal items are not repeat­ed; to this effect, each new item is com­pared with the pre­ced­ing ones.

For geeks: This is done by stor­ing pro­duc­tions in a text file which is scanned for rep­e­ti­tions. The effi­cien­cy of this method depends on the tech­nol­o­gy of the work­ing disk. A SSD is high­ly recommended!

A simple example

Let us start with a very sim­ple gram­mar "-gr.tryAllItems0" which is made up of two lay­ers of subgrammars:

-se.tryAllItems0
-al.abc

RND
gram#1[1] S --> X X X
gram#1[2] S --> X X
-----
RND
gram#2[1] X --> a
gram#2[2] X --> b

The RND instruc­tion indi­cates that the rules in the gram­mar will be select­ed ran­dom­ly until no rule applies. The first sub­gram­mar pro­duces either "X X X" or "X X", then the machine jumps to the sec­ond sub­gram­mar to replace each 'X' with either 'a' or 'b'.

In the " Produce all items" mode, rules are called in sequence, and their deriva­tions are per­formed by pick­ing up the left­most occur­rence of the left argu­ment in the work string.

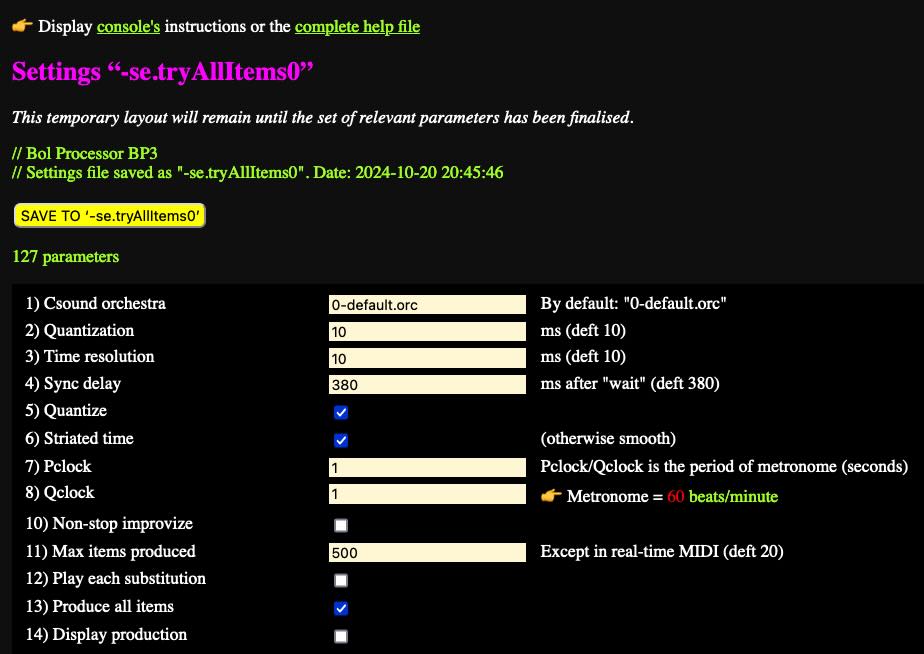
In the set­tings of " tryAllItems0 " (see pic­ture), "Produce all items" is checked. A para­me­ter " Max items pro­duced" can be used to lim­it the num­ber of productions.

The out­put is set to "BP data file" for this demo, although real-time MIDI, MIDI files and Csound score are pos­si­ble because 'a' and 'b' are defined as sound-objects. However, the sound out­put is com­plete­ly irrel­e­vant with this sim­ple grammar.

Any pro­duc­tion that still con­tains a vari­able is dis­card­ed. This nev­er hap­pens with the " tryAllItems0 " grammar.

The pro­duc­tion of this gram­mar is:

a a a
a a b
a b a
a b b
b a a
b a b
b b a
b b b
a a
a b
b a
b b

All the steps are shown on the self-explanatory trace:

S
X X X
a X X
a a X
a a a
a a b
a X a
a a a
a b a
a b X
a b a
a b b
a X b
a a b
a b b
X a X
a a X
a a a
a a b
X a a
a a a
b a a
b a X
b a a
b a b
X a b
a a b
b a b
X X a
a X a
a a a
a b a
X a a
a a a
b a a
b X a
b a a
b b a
X b a
a b a
b b a
b X X
b a X
b a a
b a b
b X a
b a a
b b a
b b X
b b a
b b b
b X b
b a b
b b b
X b X
a b X
a b a
a b b
X b a
a b a
b b a
b b X
b b a
b b b
X b b
a b b
b b b
X X b
a X b
a a b
a b b
X a b
a a b
b a b
b X b
b a b
b b b
X b b
a b b
b b b
X X
a X
a a
a b
X a
a a
b a
b X
b a
b b
X b
a b
b b

A pattern grammar

Let us mod­i­fy "-gr.tryAllItems0" as follows:

-se.tryAllItems0
-al.abc

RND
gram#1[1] S --> (= X) X (: X)
gram#1[2] S --> X X
-----
RND
gram#2[1] X --> a
gram#2[2] X --> b

The first rule gram#1[1] con­tains a pat­tern of exact rep­e­ti­tion: the third 'X' should remain iden­ti­cal to the first one. Keeping the pat­tern brack­ets, the pro­duc­tion would be:

(= a) a (: a)
(= a) b (: a)
(= b) a (: b)
(= b) b (: b)
a a
a b
b a
b b

This out­put shows that the third ter­mi­nal sym­bol is a copy of the first. These items can be played on MIDI or Csound, as the machine will remove struc­tur­al mark­ers. However, struc­tur­al mark­ers can also be delet­ed on the dis­play by plac­ing a " _destru" instruc­tion under the "RND" of the sec­ond sub­gram­mar. This yields

a a a
a b a
b a b
b b b
a a
a b
b a
b b

To become more famil­iar with pat­terns (includ­ing embed­ded forms), try "-gr.tryDESTRU" in the "ctests" fold­er.

A more complex example

Consider the fol­low­ing gram­mar "-gr.tryAllItems1" in the "ctests" fold­er:

RND
gram#1[1] S --> X Y /Flag = 2/ /Choice = 1/
-----
RND
gram#2[1] /Choice = 1/ /Flag - 1/ X --> C1 X
gram#2[2] /Choice = 2/ X --> C2 X _repeat(1)
gram#2[3] <100-50> /Choice = 3/ X --> C3 X
gram#2[4] X --> C4 _goto(3,1)
gram#2[5] Y --> D3
Gram#2[6] X --> T
-----
RND
gram#3[1] T --> C5 _failed(3,2)
gram#3[2] Y --> D6

This gram­mar uses a flag 'Choice' to select which of the rules 1, 2 or 3 will be used in sub­gram­mar #2. Just change its val­ue to try a dif­fer­ent option, as they pro­duce the same 'lan­guage'. Terminals are sim­ple notes in the English con­ven­tion: C1, C2, etc. 

The flag 'Flag' is set to 2 by the first rule. If 'Choice' is equal to 1, rule gram#2[1] is applied, and it can only be applied twice due to the decre­men­ta­tion. This ensures that the lan­guage will be finite.

Rule gram#2[4] con­tains a "_goto(3,1)" instruc­tion. Whenever it is fired, the infer­ence engine will leave sub­gram­mar #2 and jump to rule #1 of sub­gram­mar #3. If the rule is a can­di­date, it will be used and the engine will con­tin­ue to look for can­di­date rules in sub­gram­mar #3. If the gram#3[1] rule is not applic­a­ble, the engine will jump to rule #2 of sub­gram­mar #3, as instruct­ed by "_failed(3,2)". In fact, these _goto() and _failed() instruc­tion have no effect on the final pro­duc­tion, but they do mod­i­fy the trace.

If 'Choice' is equal to 2, the " _repeat(1)" instruc­tion will force the gram#2[2] rule to be applied two times. If 'Choice' is equal to 3, the rule gram#2[3] will be applied twice because it has an ini­tial weight of 100 which is reduced by 50 after each appli­ca­tion. When it reach­es zero, the rule is neutralised.

For all val­ues of 'Choice' the pro­duc­tion is:

C1 C1 C4 D6
C1 C1 C4 D3
C1 C1 C5 D3
C1 C1 C5 D6
C1 C4 D6
C1 C4 D3
C1 C5 D3
C1 C5 D6
C4 D6
C4 D3
C5 D3
C5 D6

Since you insist, here is the out­put played in real time on a Pianoteq instrument!

We hope for more con­vinc­ing musi­cal examples. 😀

Posted on

Capture MIDI input

Work in progress

Capturing MIDI input opens the way to "learn­ing" from the per­for­mance of a musi­cian or anoth­er MIDI device. The first step is to use the cap­tured incom­ing NoteOn/Noteoff events, and option­al­ly ControlChange and PitchBend events, to build a poly­met­ric struc­ture that repro­duces the stream.

The dif­fi­cul­ty of this task lies in the design of the most sig­nif­i­cant poly­met­ric struc­ture — for which AI tools may prove help­ful in the future. Proper time quan­ti­za­tion is also need­ed to avoid over­ly com­pli­cat­ed results.

We've made it pos­si­ble to cap­ture MIDI events while oth­er events are play­ing. For exam­ple, the out­put stream of events can pro­vide a frame­work for the tim­ing of the com­pos­ite per­for­mance. Consider, for instance, the tem­po set by a bass play­er in a jazz improvisation.

The _capture() command

A sin­gle com­mand is used to enable/disable a cap­ture: _capture(x), where x (in the range 1…127) is an iden­ti­fi­er of the 'source'. This para­me­ter will be used lat­er to han­dle dif­fer­ent parts of the stream in dif­fer­ent ways.

_capture(0) is the default set­ting: input events are not recorded.

The cap­tured events and the events per­formed on them are stored in a 'cap­ture' file in the temp_bolprocessor fold­er. This file is processed by the interface.

(Examples are found in the project "-da.tryCapture".)

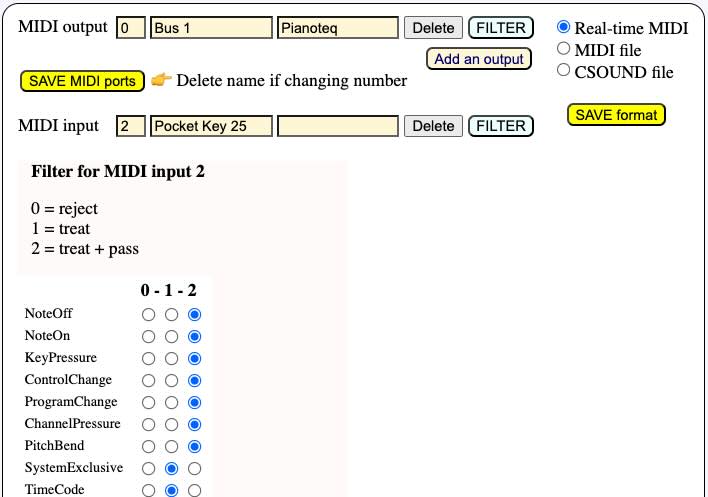
The first step to use _capture() is to set up the MIDI input and more specif­i­cal­ly its fil­ter. It should at least treat NoteOn and NoteOff events. ControlChange and PitchBend mes­sages can also be captured.

If the pass option is set (see pic­ture), incom­ing events will also be heard on the out­put MIDI device. This is use­ful if the input device is a silent device.

It is pos­si­ble to cre­ate sev­er­al inputs con­nect­ed to sev­er­al sources of MIDI events, each one with its own fil­ter set­tings. Read the Real-time MIDI page for more explanations.

Another impor­tant detail is the quan­ti­za­tion set­ting. If we want to con­struct poly­met­ric struc­tures, it may be impor­tant to set the data to the near­est mul­ti­ple of a fixed dura­tion, typ­i­cal­ly 100 mil­lisec­onds. This can be set in the set­tings file "-se.tryCapture".

Simple example

Let us take a look at a very sim­ple exam­ple of a cap­ture on top of a performance.

C4 _D4 _capture(104) E4 F4 G4 _capture(0) A4 B4

The machine will play the sequence of notes C4 D4 E4 F4 G4 A4 B4. It will lis­ten to the input while play­ing E4 F4 G4. It will record both the sequence E4 F4 G4 and the notes received from a source tagged "104".

Suppose that the sequence G3 F3 D3 was played on top of E4 F4 G4. The cap­ture file might look like this:

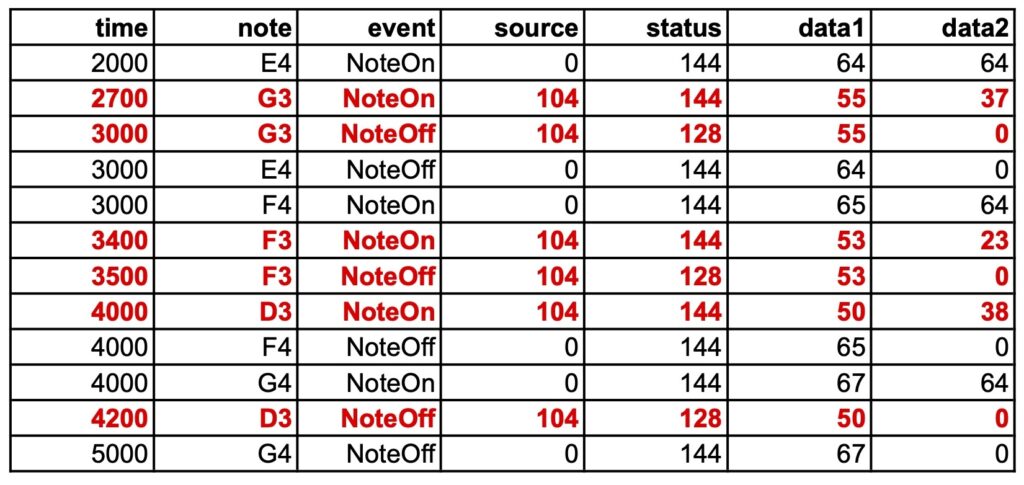
It should be not­ed that all the dates are approx­i­mat­ed to mul­ti­ples of 100 mil­lisec­onds, i.e. the quan­ti­za­tion. For exam­ple, the NoteOff of input note G3 falls exact­ly on the date 3000 ms, which is the NoteOff of the played note E4.

The record­ing of input and played notes starts at note E4 and ends at note G4, as spec­i­fied by _capture(104) and _capture(0).

An accept­able approx­i­ma­tion of this sequence would be the poly­met­ric expression:

C4 D4 {E4 F4 G4, - - G3 - F3 - D3 - -} A4 B4

Approximations will be auto­mat­i­cal­ly cre­at­ed from the cap­ture files at a lat­er stage.

Pause and capture

MIDI input will con­tin­ue to be cap­tured and timed cor­rect­ly after the Pause but­ton is clicked. This makes it pos­si­ble to play the begin­ning of a piece of music and stop exact­ly where an input is expected.

Combining 'wait' instructions

Try:

_script(wait for C3 channel 1) C4 D4 _capture(104) E4 F4 G4 _script(wait for D3 channel 1) _capture(0) A4 B4

The record­ing takes place dur­ing the exe­cu­tion of E4 F4 G4 and dur­ing the unlim­it­ed wait­ing time for note D3. This allows events to be record­ed even when no events are being played.

The C3 and D3 notes have been used for ease of access on a sim­ple key­board. The dates in the cap­ture file are not incre­ment­ed by the wait times.

The fol­low­ing is a set­up for record­ing an unlim­it­ed sequence of events while no event is being played. Note C0 will not be heard as it has a veloc­i­ty of zero. Recording ends when the STOP or PANIC but­ton is clicked.

_capture(65) _vel(0) C0 _script(wait forever) C0

Interpreting the record­ed input as a poly­met­ric struc­ture will be made more com­plex by the fact that no rhyth­mic ref­er­ence has been provided.

Microtonal corrections

In the fol­low­ing exam­ple, both input and out­put receive micro­ton­al cor­rec­tions of the just into­na­tion scale.

_scale(just intonation,0) C4 D4 _capture(104) E4 F4 G4 A4 _capture(0) B4

Below is a cap­ture file obtained by enter­ing G3 F3 D3 over the sequence E4 F4 G4 A4. Note the pitch­bend cor­rec­tions in the last col­umn, which indi­cate micro­ton­al adjust­ments. The rel­e­vant val­ues are those that pre­cede NoteOns on the same channel.

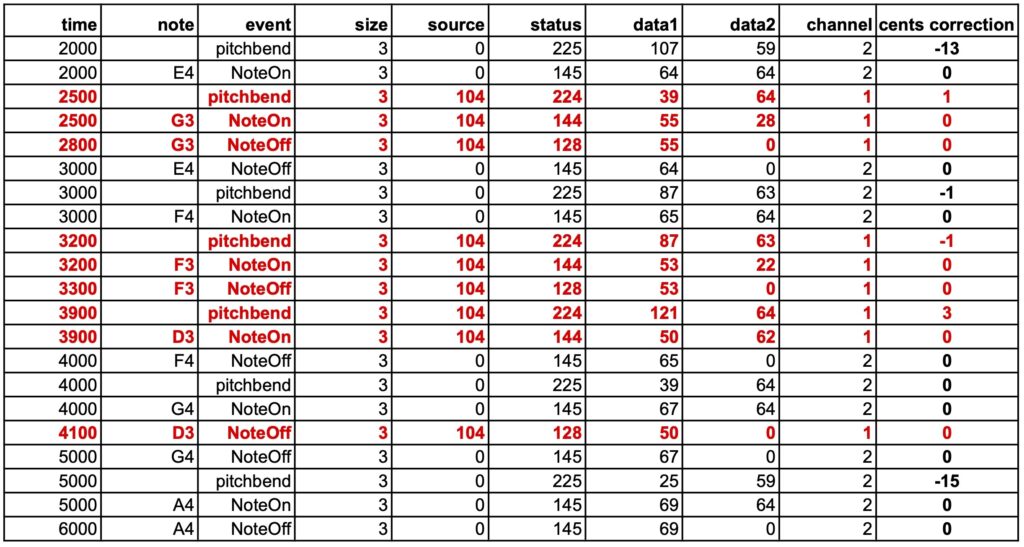
The out­put events (source 0) are played on MIDI chan­nel 2, and the input events (source 104) on MIDI chan­nel 1. More chan­nels will be used if out­put notes have an over­lap — see the page MIDI micro­tonal­i­ty. In this way, pitch­bend com­mands and the notes they address are dis­trib­uted across dif­fer­ent channels.

Added pitchbend

In the fol­low­ing exam­ple, a pitch­bend cor­rec­tion of +100 cents is applied to the entire piece. It does mod­i­fy out­put events, but it has no effect on input events.

_pitchrange(200) _pitchbend(+100) _scale(just intonation,0) C4 D4 _capture(104) E4 F4 G4 A4 _capture(0) B4

Again, after play­ing G3 F3 D3 over the sequence E4 F4 G4 A4:

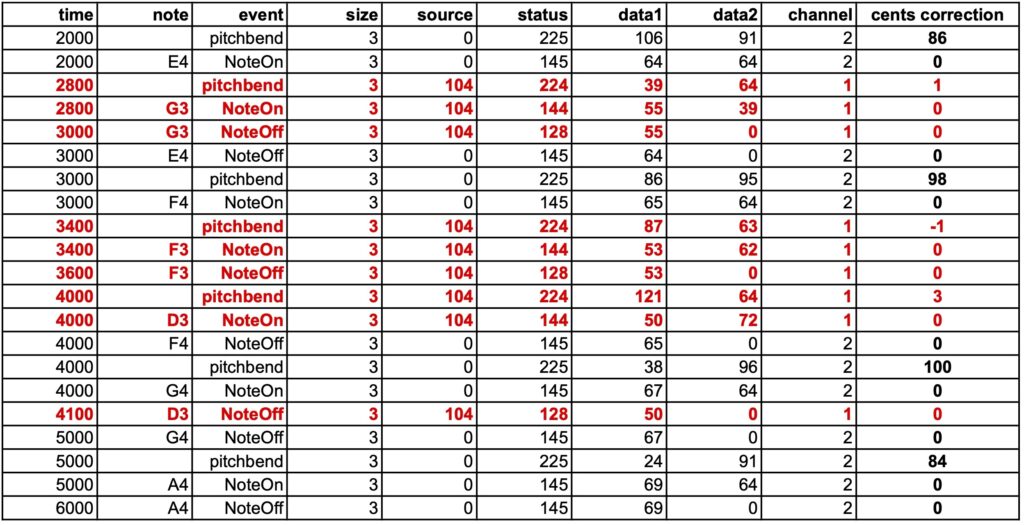
Pitchbend cor­rec­tions applied to the input (source 104) are only those induced by the micro­ton­al scale. Pitchbend cor­rec­tions applied to the out­put (source 0) are the com­bi­na­tion of micro­ton­al adjust­ments (see pre­vi­ous exam­ple) and the +100 cents of the pitch­bend command.

Capturing and recording more events

The _capture() com­mand allows you to cap­ture most types of MIDI events: all 3-byte types, and the 2-byte type Channel pres­sure (also called Aftertouch).

Below is a (com­plete­ly unmu­si­cal) exam­ple of cap­tur­ing dif­fer­ent messages.

The cap­ture will take place in a project called "-da.tryReceive":

_script(wait for C0 chan­nel 1) _capture(111) D4 _pitchrange(200) _pitchbend(+50) _press(35) _mod(42) D4 _script(wait forever)

The record­ing will have a "111" mark­er to indi­cate which events have been received. Only two notes D4 are played dur­ing the record­ing, the sec­ond one is raised by 50 cents and has a chan­nel pres­sure of 35 and a mod­u­la­tion of 42.

After play­ing back the two D4s, the machine will wait until the STOP but­ton is clicked. This gives the oth­er machine time to send its own data and have it recorded.

The sec­ond machine is anoth­er instance of BP3 — actu­al­ly anoth­er tag on the interface's brows­er with the "-da.trySend" project:

{_vel(0) <<C0>>} G3 _press(69) _mod(5430) D3 _pitchrange(200) _pitchbend(+100) E3

This project will start by send­ing "{_vel(0) <<C0>>} " which is the note C0 with veloc­i­ty 0 and dura­tion null (an out-time object). This will trig­ger "-da.tryReceive" which wait­ed for C0. The curly brack­ets {} restrict veloc­i­ty 0 to the note C0. Outside of this expres­sion, the veloc­i­ties are set to their default val­ue (64). In this data, chan­nel pres­sure, mod­u­la­tion and a pitch­bend cor­rec­tion of +100 cents are applied to the final note E3.

The result­ing sound is ter­ri­ble, you've been warned:

Performed and cap­tured events. Forget the way it sounds and look at the file below!

However, the 'cap­ture' file shows that all events have been cor­rect­ly recorded:

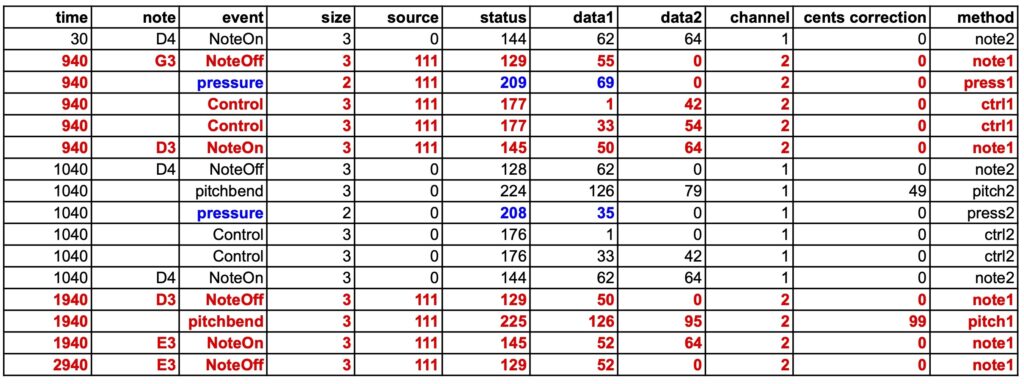
Captured events (from "-da.trySend") are coloured red. They have been auto­mat­i­cal­ly assigned to MIDI chan­nel 2, so that cor­rec­tions will not be mixed between per­for­mance and reception.

The pitch­bend cor­rec­tions are shown in the "cents cor­rec­tion" col­umn, each applied to its own channel.

The chan­nel pres­sure cor­rec­tions (coloured blue) dis­play the expect­ed val­ues. The mod­u­la­tion cor­rec­tions (in the range 0 to 16383) are divid­ed into two 3-byte mes­sages, the first car­ry­ing the MSB and the sec­ond the LSB.

There is a time mis­match of approx­i­mate­ly 150 mil­lisec­onds between the expect­ed and actu­al dates, but the dura­tions of the notes are accu­rate. The mis­match is caused by the delay in the trans­mis­sion of events over the vir­tu­al port. The data looks bet­ter if the quan­ti­za­tion in the "-da.tryReceive" project is set to 100 ms instead of 10 ms. However, this is of minor impor­tance, as a "nor­mal­i­sa­tion" will take place dur­ing the (forth­com­ing) analy­sis of the "cap­ture" file.

For geeks: The last col­umn indi­cates where events have been record­ed in the pro­ce­dure sendMIDIEvent(), file MIDIdriver.c.

Capture events without the need to perform

The set­up of the "-da.tryReceive" project should be for example:

_capture(99) _vel(0) C4 _script(wait forever)

Note C4 is not heard due to its veloc­i­ty 0. It is fol­lowed with all MIDI events received by the input until the STOP but­ton is clicked. This makes it pos­si­ble to record an entire per­for­mance. The pro­ce­dure can also be checked with items pro­duced and per­formed by the Bol Processor.

Note that the inclu­sion of pitch­bend mes­sages makes it pos­si­ble to record music played on micro­ton­al scales and (hope­ful­ly) iden­ti­fy the clos­est tun­ings suit­able for repro­duc­tion of the piece of music.

For exam­ple, try to cap­ture the fol­low­ing phrase from Oscar Peterson's Watch What Happens:

_tempo(2) {4, {{2, F5 Bb4 C5 C4} {3/2, D4} {1/2, Eb4 Db4 D4}, {F4, C5} {1/2, F4, G4} {1/2, F3, G3} {2, Gb3}}}, {4, {C4 {1, Bb3 Bb2} {2, A2}, {D3, A3} {1, Eb3 Eb2} {2, D2}}}

This phrase was import­ed from a MusicXML score (read page)

A dia­logue box appears to analyse or down­load the cap­tured data:

The result is com­plex, but it's going to lend itself to being analysed automatically.

The raw table is avail­able to down­load (as an image) here. The cur­rent analy­sis of this exam­ple is avail­able here.

Once the ori­gin of dates has been set to the first NoteOn or NoteOff received, the result is — only impor­tant columns are dis­played: time, note, event, key, velocity:

This pianoroll rep­re­sents the input data pro­duced by play­ing Oscar Peterson's phrase on the Bol Processor (file -da.trySend). The cap­tured data is slight­ly dif­fer­ent in the last part.

0 F5 NoteOn 77 64
0 F4 NoteOn 65 64
0 C5 NoteOn 72 64
0 C4 NoteOn 60 64
0 D3 NoteOn 50 64
0 A3 NoteOn 57 64
230 F5 NoteOff 77 0
230 Bb4 NoteOn 70 64
470 Bb4 NoteOff 70 0
470 C5 NoteOff 72 0
470 C5 NoteOn 72 64
470 F4 NoteOff 65 0
470 C5 NoteOff 72 0
470 F4 NoteOn 65 64
470 G4 NoteOn 67 64
470 C4 NoteOff 60 0
470 Bb3 NoteOn 58 64
470 D3 NoteOff 50 0
470 A3 NoteOff 57 0
470 Eb3 NoteOn 51 64
710 C5 NoteOff 72 0
710 C4 NoteOn 60 64
710 F4 NoteOff 65 0
710 G4 NoteOff 67 0
710 F3 NoteOn 53 64
710 G3 NoteOn 55 64
710 Bb3 NoteOff 58 0
710 Bb2 NoteOn 46 64
710 Eb3 NoteOff 51 0
710 Eb2 NoteOn 39 64
960 C4 NoteOff 60 0
960 D4 NoteOn 62 64
960 F3 NoteOff 53 0
960 G3 NoteOff 55 0
960 F#3 NoteOn 54 64
960 Bb2 NoteOff 46 0
960 A2 NoteOn 45 64
960 Eb2 NoteOff 39 0
960 D2 NoteOn 38 64
1730 D4 NoteOff 62 0
1730 Eb4 NoteOn 63 64
1830 Eb4 NoteOff 63 0
1830 C#4 NoteOn 61 64
1880 C#4 NoteOff 61 0
1880 D4 NoteOn 62 64
1960 D4 NoteOff 62 0
1960 F#3 NoteOff 54 0
1960 A2 NoteOff 45 0
1960 D2 NoteOff 38 0

The next task on our agen­da will be to analyse the 'cap­tured' file and recon­struct the orig­i­nal poly­met­ric expres­sion (shown above) or an equiv­a­lent ver­sion. Then we can con­sid­er mov­ing on to gram­mars, sim­i­lar to what we've done with import­ed MusicXML scores (read page).

Constructing a poly­met­ric expres­sion from an arbi­trary stream of notes will hope­ful­ly be achieved with the help of graph neur­al net­works. The idea is to train the lan­guage mod­el with a set of sound files, MIDI files, and their 'trans­la­tions' as poly­met­ric expres­sions. Read the AI recog­ni­tion of poly­met­ric nota­tion page to fol­low this approach.