Raga intonation

This arti­cle demon­strates the the­o­ret­i­cal and prac­ti­cal con­struc­tion of micro­ton­al scales for the into­na­tion of North Indian ragas, using tools avail­able with the Bol Processor (BP3) + Csound.

It is intend­ed to com­ple­ment the pages Microtonality and Just into­na­tion, a gen­er­al frame­work and The Two-vina exper­i­ment. However, its under­stand­ing does not require a pri­or study of these relat­ed pages.

This raga into­na­tion exer­cise demon­strates BP3’s abil­i­ty to han­dle sophis­ti­cat­ed mod­els of micro-intonation and to sup­port the fruit­ful cre­ation of music embody­ing these models.

Theory versus practice

To sum­marise the back­ground, the frame­work for con­struct­ing ‘just into­na­tion’ scales is a deci­pher­ing of the first six chap­ters of the Nāṭyaśāstra, a Sanskrit trea­tise on music, dance and dra­ma dat­ing from a peri­od between 400 BC and 200 AD. For con­ve­nience, we call it “Bharata’s Model”, although there is no his­tor­i­cal record of a sin­gle author by that name.

Using exclu­sive infor­ma­tion dri­ven from the text and its descrip­tion of the Two-vina exper­i­ment, an infi­nite num­ber of valid inter­pre­ta­tions of the ancient the­o­ry are pos­si­ble, as shown in A Mathematical Discussion of the Ancient Theory of Scales accord­ing to Natyashastra (Bel 1988a). Among these, the one advo­cat­ed by many musi­col­o­gists — influ­enced by west­ern acoustics and scale the­o­ries — is that the fre­quen­cy ratio of the har­mon­ic major third would be 5/4. This is equiv­a­lent to set­ting the fre­quen­cy ratio of the syn­ton­ic com­ma at 81/80.

Although this inter­pre­ta­tion pro­vides a con­sis­tent mod­el for just into­na­tion har­mo­ny - see Just into­na­tion, a gen­er­al frame­work — it would be a stretch to claim that the same applies to raga into­na­tion. Accurate assess­ment of raga per­for­mance using our Melodic Movement Analyser (MMA) in the ear­ly 1980s revealed that melod­ic struc­tures derived from sta­tis­tics (using selec­tive tona­grams, see below) often dif­fer sig­nif­i­cant­ly from the scales pre­dict­ed by the “just into­na­tion” inter­pre­ta­tion of Bharata’s mod­el. Part of the expla­na­tion may be the strong har­mon­ic attrac­tion of drones (tan­pu­ra) played in the back­ground of raga performances.

Speaking of gra­ma-s (scale frame­works) in the ancient Indian the­o­ry, E.J. Arnold wrote (1982 p. 40):

Strictly speak­ing the gra­mas belong to that aspect of nada (vibra­tion) which is ana­ha­ta (“unstruck”). That means to say that the “gra­ma” can nev­er be heard as a musi­cal scale [as we did on page Just into­na­tion, a gen­er­al frame­work]. What can be heard as a musi­cal scale is not the gra­ma, but any of its mur­ccha­nas.

Once elec­tron­ic devices such as the Shruti Harmonium (1979) and the Melodic Movement Analyser (1981) became avail­able, the chal­lenge for raga into­na­tion research was to rec­on­cile two method­olo­gies: a top-down approach, test­ing hypo­thet­i­cal mod­els against data, and a data-driven bottom-up approach.

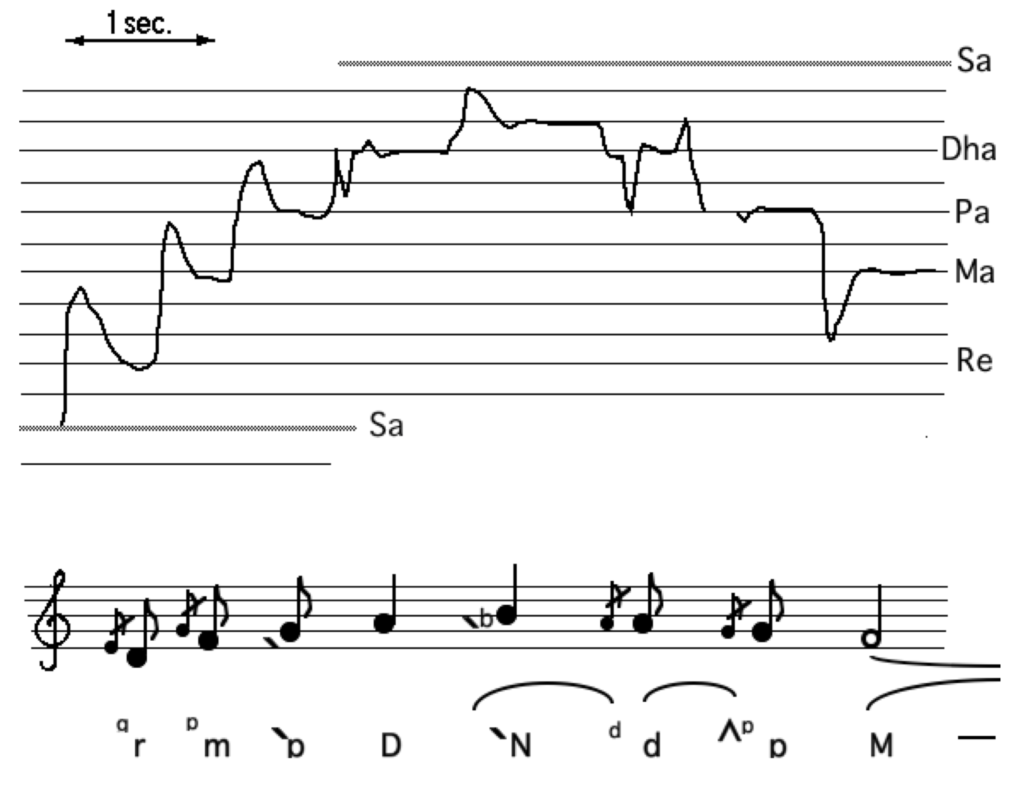
The “micro­scop­ic” obser­va­tion of melod­ic lines (now eas­i­ly ren­dered by soft­ware such as Praat) has con­firmed the impor­tance of note treat­ment (orna­men­ta­tion, alankara) and tem­po­ral dimen­sions of raga that are not tak­en into account by scale the­o­ries. For exam­ple, the ren­der­ing of the note ‘Ga’ in raga Darbari Kanada (Bel & Bor 1984; van der Meer 2019) and the typ­i­cal treat­ment of notes in oth­er ragas (e.g. Rao & Van der Meer 2009; 2010) have been dis­cussed at length. The visu­al tran­scrip­tion of a phrase from raga Asha illus­trates this:

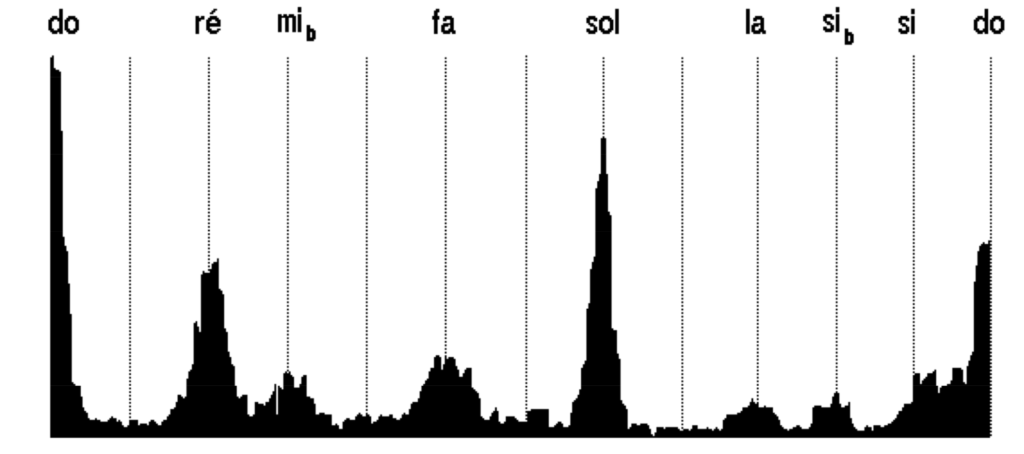
To extract scale infor­ma­tion from this melod­ic con­tin­u­um, a sta­tis­ti­cal mod­el was imple­ment­ed to show the dis­tri­b­u­tion of pitch over an octave. The image shows the tona­gram of a 2-minute sketch (cha­lana) of raga Sindhura taught by Pandit Dilip Chandra Vedi.

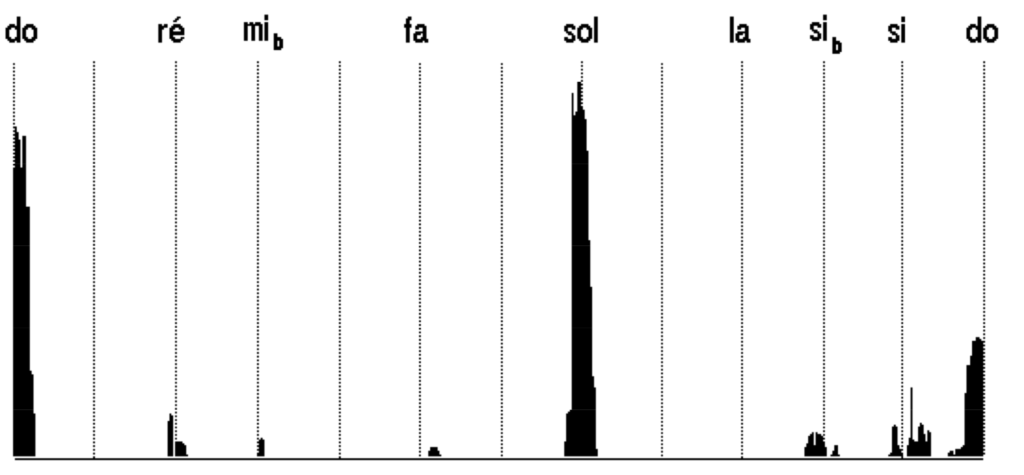
The same melod­ic data was processed again after fil­ter­ing through 3 win­dows that attempt­ed to iso­late ‘sta­ble’ parts of the line. The first win­dow, typ­i­cal­ly 0.1 sec­onds, would elim­i­nate irreg­u­lar seg­ments, the sec­ond (0.4 sec­onds) would dis­card seg­ments out­side a rec­tan­gle of 80 cents height, and the third was used for aver­ag­ing. The result is a “skele­ton” of the tonal scale, dis­played as a selec­tive tona­gram.

These results would often not match the scale met­rics pre­dict­ed by the ‘just into­na­tion’ inter­pre­ta­tion of Bharata’s mod­el. Continuing with this data-driven approach, we pro­duced the (non-selective) tona­grams of 30 ragas (again, chalana-s) to com­pute a clas­si­fi­ca­tion based on their tonal mate­r­i­al. Dissimilarities between pairs of graphs (com­put­ed using Kuiper’s algo­rithm) were approx­i­mat­ed as dis­tances, from which a 3-dimensional clas­si­cal scal­ing was extracted:

This exper­i­ment sug­gests that con­tem­po­rary North-Indian ragas are amenable to mean­ing­ful auto­mat­ic clas­si­fi­ca­tion on the basis of their (time-independent) inter­val­ic con­tent alone. This approach is anal­o­gous to human face recog­ni­tion tech­niques, which are able to iden­ti­fy relat­ed images from a lim­it­ed set of features.

This impres­sive clas­si­fi­ca­tion has been obtained by sta­tis­ti­cal analy­sis of sta­t­ic rep­re­sen­ta­tions of raga per­for­mance. This means that the same result would be obtained by play­ing the sound file in reverse, or even by slic­ing it into seg­ments reassem­bled in a ran­dom order… Music is a dynam­ic phe­nom­e­non that can­not be reduced to tonal “inter­vals”. Therefore, sub­se­quent research into the rep­re­sen­ta­tion of the melod­ic lines of raga — once it could be effi­cient­ly processed by 100% dig­i­tal com­put­ing — led to the con­cept of Music in Motion, i.e. syn­chro­nis­ing graphs with sounds so that the visu­als reflect the music as it is being heard, arguably the only appropriate“notation” for raga (Van der Meer & Rao 2010; Van der Meer 2020).

This graph mod­el is prob­a­bly a great achieve­ment as an edu­ca­tion­al and doc­u­men­tary tool, indeed the envi­ron­ment I dreamed of when design­ing the Melodic Movement Analyser. However, to pro­mote it as a the­o­ret­i­cal mod­el is the con­tin­u­a­tion of a west­ern selec­tive bias. As far as I know, no Indian music mas­ter has ever attempt­ed to describe the intri­ca­cies of raga using hand-drawn mel­o­grams, although they could. The fas­ci­na­tion with tech­nol­o­gy — and west­ern ‘sci­ence’ in gen­er­al — is no indi­ca­tion of its rel­e­vance to ancient Indian concepts.

Music is judged by ears; there­fore, a the­o­ry of music should be judged by its abil­i­ty to pro­duce musi­cal sounds via pre­dic­tive model(s). Numbers, charts and graphs are mere­ly tools for inter­pret­ing and pre­dict­ing sound phe­nom­e­na. This approach is called analy­sis by syn­the­sis in Daniel Hirst’s book on speech prosody. (Hirst, 2022, forth­com­ing, p. 137):

Analysis by syn­the­sis involves try­ing to set up an explic­it pre­dic­tive mod­el to account for the data which we wish to describe. A mod­el, in this sense, is a sys­tem which can be used for analy­sis — that is deriv­ing a (sim­ple) abstract under­ly­ing rep­re­sen­ta­tion from the (com­pli­cat­ed) raw acoustic data. A mod­el which can do this is explic­it but it is not nec­es­sar­i­ly pre­dic­tive and empir­i­cal­ly testable. To meet these addi­tion­al cri­te­ria, the mod­el must also be reversible, that is it must be pos­si­ble to use the mod­el to syn­the­sise observ­able data from the under­ly­ing representation.

This is the rai­son d’être for the fol­low­ing investigation.

Microtonal framework

The “flex­i­ble” mod­el derived from the the­o­ret­i­cal mod­el of Natya Shastra (see The Two-vina exper­i­ment) rejects the claim of a pre­cise fre­quen­cy ratio for the har­mon­ic major third clas­si­fied in ancient lit­er­a­ture as anu­va­di (aso­nant). This amounts to admit­ting that the syn­ton­ic com­ma (pramāņa ṣru­ti in Sanskrit) could take any val­ue between 0 and 56.8 cents.

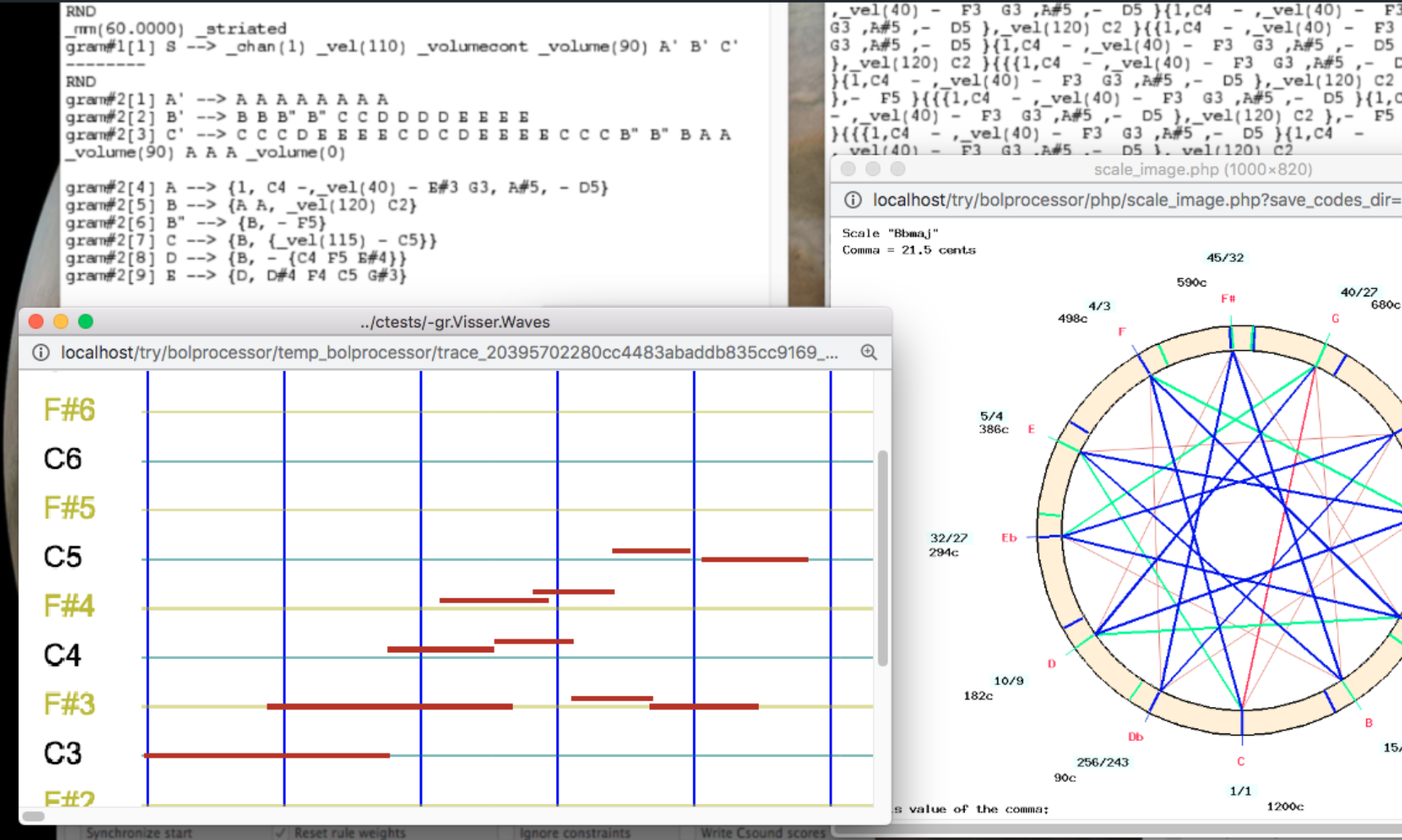
Let us look at some graph­i­cal rep­re­sen­ta­tions (from the Bol proces­sor) to illus­trate these points.

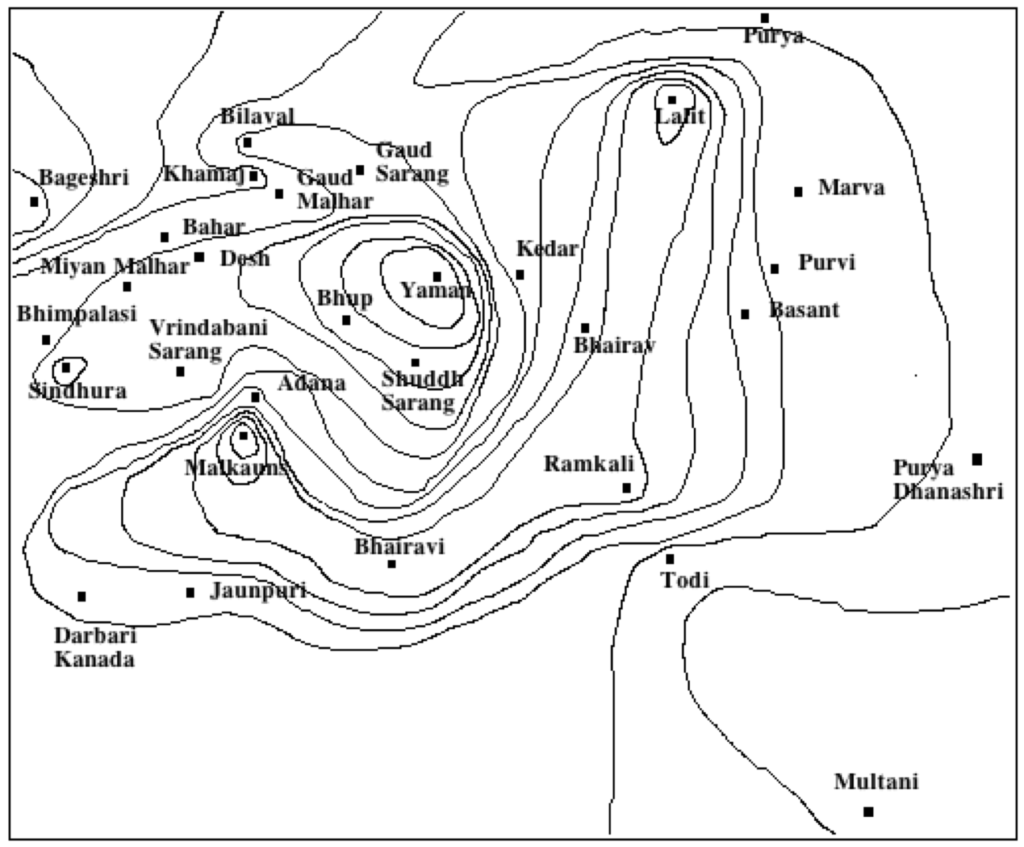
The basic frame­work of musi­cal scales, accord­ing to Indian musi­col­o­gy, is a set of 22 tonal posi­tions in the octave called shru­ti-s in ancient texts. Below is the frame­work dis­played by the Bol Processor (micro­ton­al scale “gra­ma”) with a 81/80 syn­ton­ic com­ma. The names of the posi­tions “r1_”, “r2_”, etc. fol­low the con­straints of low­er case ini­tials and the addi­tion of an under­score to dis­tin­guish octave num­bers. Positions “r1” and “r2” are two ways of locat­ing komal Re (“Db” or “re bemol”), while “r3” and “r4” denote shud­dha Re (“D” or “re”), etc.

These 22 shru­ti-s can be heard on the page Just into­na­tion, a gen­er­al frame­work, bear­ing in mind (see above) that this is a frame­work and not a scale. No musi­cian would ever attempt to play or sing these posi­tions as “notes”!

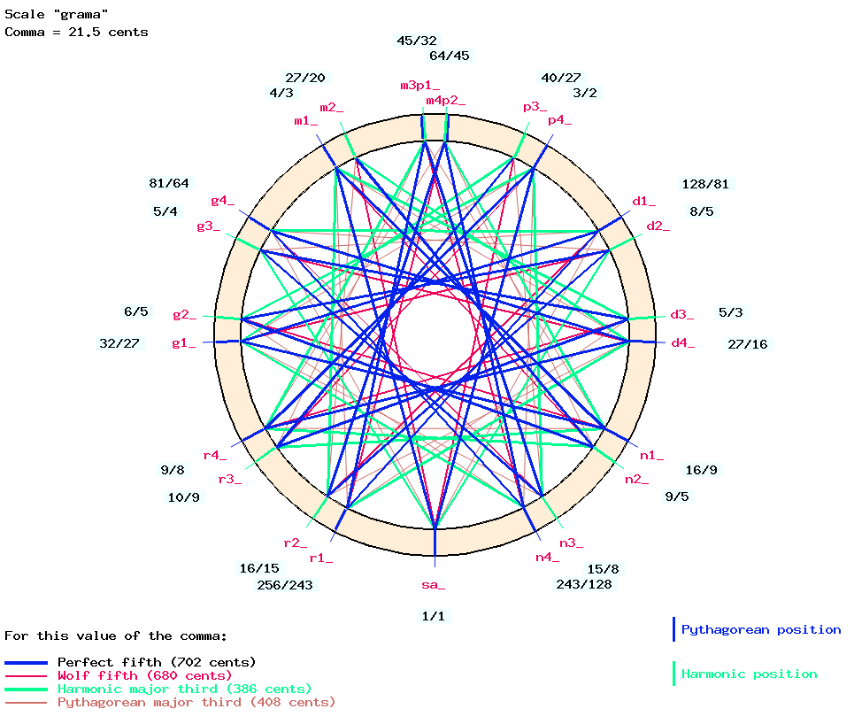
What hap­pens if the val­ue of the syn­ton­ic com­ma is changed? Below is the same frame­work with a com­ma of 0 cent. In this case, any “har­mon­ic posi­tion” — one whose frac­tion con­tains a mul­ti­ple of 5 — moves to its near­est Pythagorean neigh­bour (only mul­ti­ples of 3 and 2). The result is a “Pythagorean tun­ing”. At the top of the cir­cle, the remain­ing gap is a Pythagorean com­ma. The posi­tions are slight­ly blurred because of the mis­match­es asso­ci­at­ed with a very small inter­val (the schis­ma).

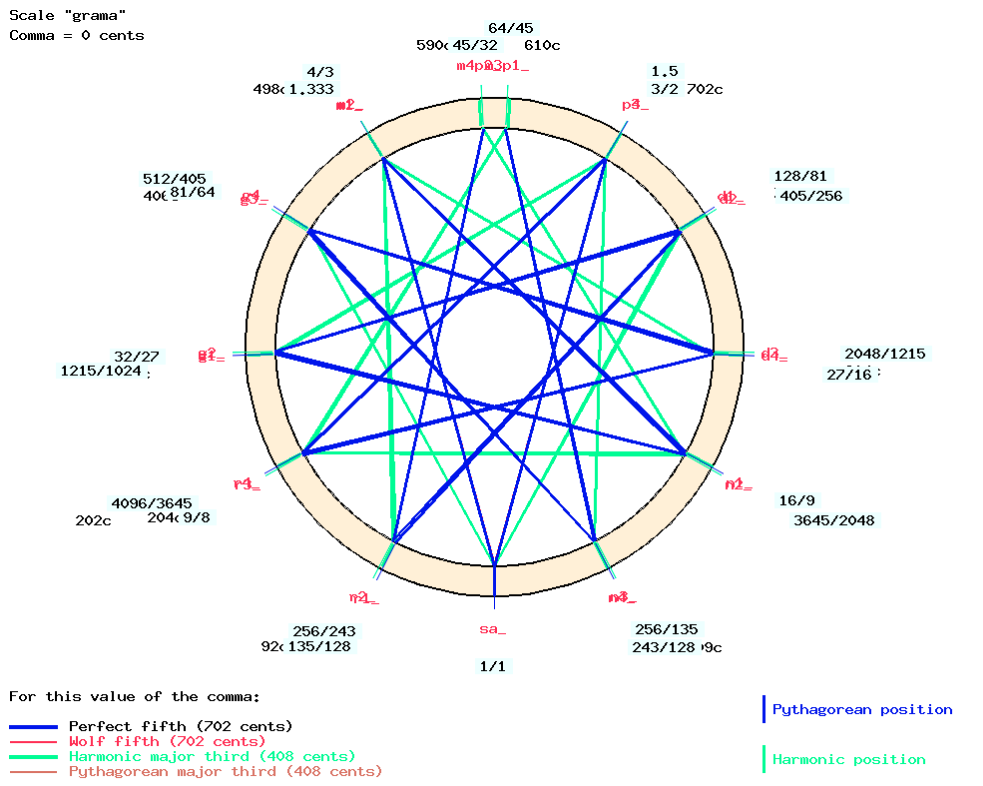
Below is the frame­work with a syn­ton­ic com­ma of 56.8 cents (its upper limit):

In this rep­re­sen­ta­tion, “har­mon­ic major thirds” of 351 cents would most like­ly sound “out of tune” because the 5/4 ratio yields 384 cents. In fact, “g2” and “g3” are both dis­tant by a quar­ter tone between Pythagorean “g1” (32/27) and Pythagorean “g4” (81/64). Nevertheless, the inter­nal con­sis­ten­cy of this frame­work (count­ing per­fect fifths in blue) makes it suit­able for con­struct­ing musi­cal scales.

Between these lim­its of 0 and 56.8 cents, the graph­ic rep­re­sen­ta­tion of the scales and their inter­nal tonal struc­ture remain unchanged, bear­ing in mind that the size of the major-third inter­vals is deter­mined by the syn­ton­ic comma.

Construction of scale types

The mod­el tak­en from Bharata’s Natya Shastra is not an obvi­ous ref­er­ence for pre­scrib­ing raga into­na­tion, as this musi­cal genre came into exis­tence a few cen­turies later.

Most of the back­ground knowl­edge required for the fol­low­ing pre­sen­ta­tion is bor­rowed from Bose (1960) and my late col­league E. James Arnold who pub­lished A Mathematical mod­el of the Shruti-Swara-Grama-Murcchana-Jati System (Journal of the Sangit Natak Akademi, New Delhi 1982). Arnold stud­ied Indian music in Banaras and Delhi in the 1970s and the ear­ly 1980s.

Bose was con­vinced (1960 p. 211) that the scale called Kaishika Madhyama was equiv­a­lent to a “just-intonation” seven-degree scale of west­ern musi­col­o­gy. In oth­er words, he took it for grant­ed that the 5/4 fre­quen­cy ratio (har­mon­ic major third) should be equiv­a­lent to the 7-shru­ti inter­val, but this state­ment had no influ­ence on the rest of his analysis.

Arnold (1982 p. 17) imme­di­ate­ly used inte­ger ratios to con­struct inter­vals with the fixed syn­ton­ic com­ma (81/80), but, as sug­gest­ed above, this does not affect his mod­el in terms of its struc­tur­al descrip­tion. He insist­ed on set­ting up a “geo­met­ric mod­el” rather than a spec­u­la­tive descrip­tion based on num­bers, as many authors (e.g. Alain Daniélou) had attempt­ed. The most inno­v­a­tive aspect of Arnold’s study was the use of a cir­cu­lar slid­ing mod­el to illus­trate the match­ing of inter­vals in trans­po­si­tion process­es (murcchana-s) - see page The Two-vina exper­i­ment.

In real­i­ty, it would be more con­ve­nient to con­tin­ue to express all inter­vals in num­bers of shruti-s, in accor­dance with the ancient Indian the­o­ry, but a machine needs met­ric data to draw graph­ics of scales. For this rea­son, we show graphs with a syn­ton­ic com­ma of 81/80, keep­ing in mind the pos­si­bil­i­ty of chang­ing this val­ue later.

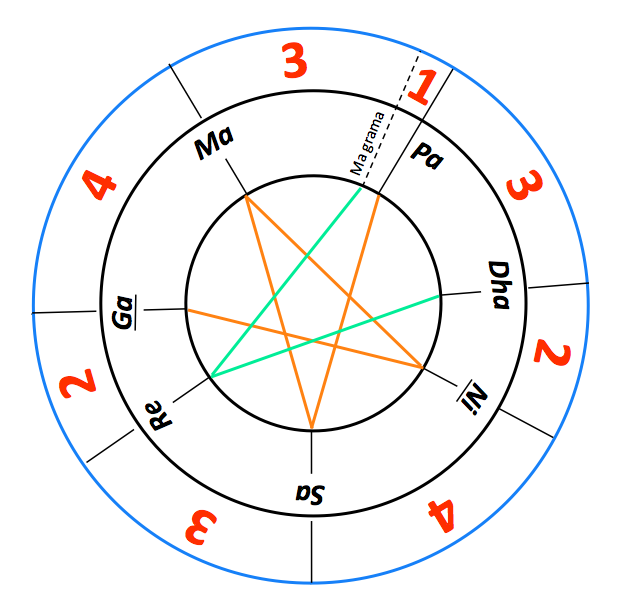
The 22-shru­ti frame­work offers the pos­si­bil­i­ty of con­struct­ing 2¹¹ = 2048 chro­mat­ic scales, of which only 12 are “opti­mal­ly con­so­nant”, i.e. con­tain only one wolf’s fifth (small­er by 1 syn­ton­ic com­ma = 22 cents).

The build­ing blocks of the tonal sys­tem accord­ing to tra­di­tion­al Indian musi­col­o­gy are two seven-degree scales called Ma-grama and Sa-grama. Bose (1960 p. 13) writes: the Shadja Grāma devel­oped from the ancient tetra­chord in which the hymns of the Sāma Veda were chant­ed. Later on anoth­er scale, called the Madhyama Grāma, was added to the sec­u­lar musi­cal sys­tem. The two scales (Dorian modes, in west­ern ter­mi­nol­o­gy) dif­fer in the posi­tion of Pa (“G” or “sol”) which may dif­fer by a syn­ton­ic com­ma (pramāņa ṣru­ti). In the Sa-grama, the inter­val Sa-Pa is a per­fect fifth (13 shru­ti-s) where­as in the Ma-grama it is a wolf’s fifth (12 shru­ti-s). Conversely, the inter­val Pa-Re is a per­fect fifth in Ma-grama and a wolf’s fifth in Sa-grama.

Bharata used the Sa-grama to expose his thought exper­i­ment (The Two vinas) aimed at deter­min­ing the sizes of shru­ti-s. He then intro­duced two addi­tion­al notes: kakali Nishada (komal Ni or “Bflat”) and antara Gandhara (shud­dh Ga or “E”) to obtain a nine-degree scale from which “opti­mal­ly con­so­nant” chro­mat­ic scales could be derived from modal trans­po­si­tions (mur­ccha­na). The process of con­struct­ing these 12 chro­mat­ic scales, name­ly “Ma01″, “Ma02″… “Sa01″, “Sa20″, etc., is explained on the page Just into­na­tion, a gen­er­al frame­work.

The selec­tion of notes in each chro­mat­ic scale pro­duces 5 to 7 note melod­ic types. In Natya Shastra these melod­ic types are called jāti. These can be seen as the ances­tors of ragas, although their lin­eages and struc­tures are only spec­u­la­tive (read on). The term thāṭ (pro­nounced ‘taat’) — trans­lat­ed as ‘mode’ or ‘par­ent scale’ — was lat­er adopt­ed, each thāṭ being called by the name of a raga (see Wikipedia). Details of the process, ter­mi­nol­o­gy and sur­veys of sub­se­quent musi­co­log­i­cal lit­er­a­ture can be found in pub­li­ca­tions by Bose and oth­er scholars.

The con­struc­tion of the basic scale types is explained by Arnold (1982 p. 37-38). The start­ing point is the chro­mat­ic Ma-grama in its basic posi­tion — name­ly “Sa_murcchana” in the “-cs.12_scales” Csound resource file. This scale can be visu­alised, using Arnold’s slid­ing mod­el, by plac­ing the S note of the inner wheel on the S of the out­er crown :

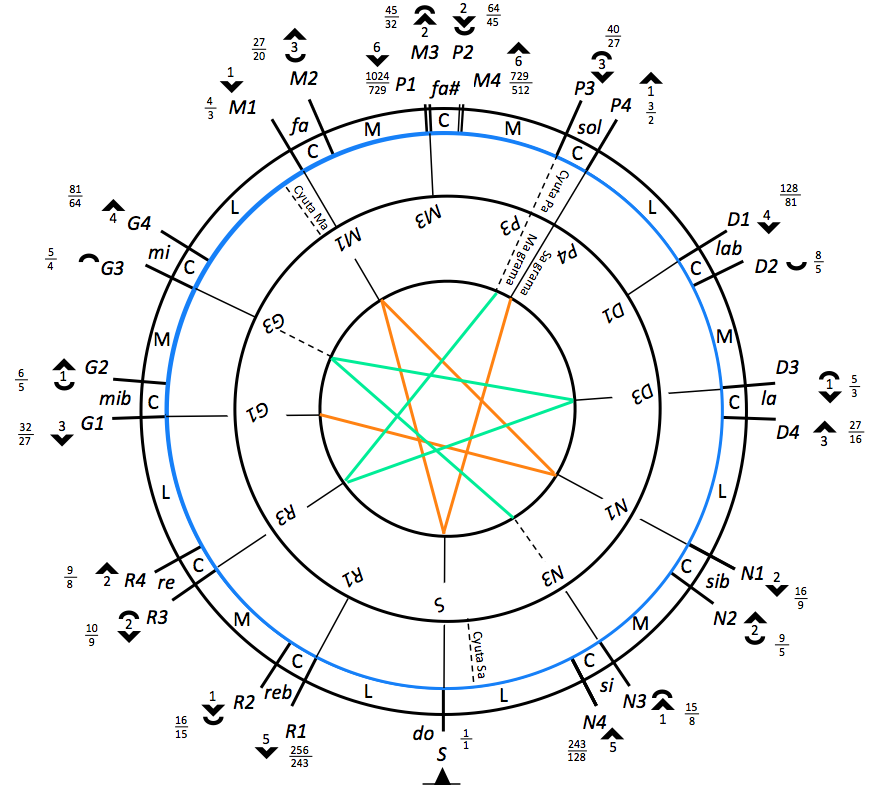
This yields the fol­low­ing intervals:

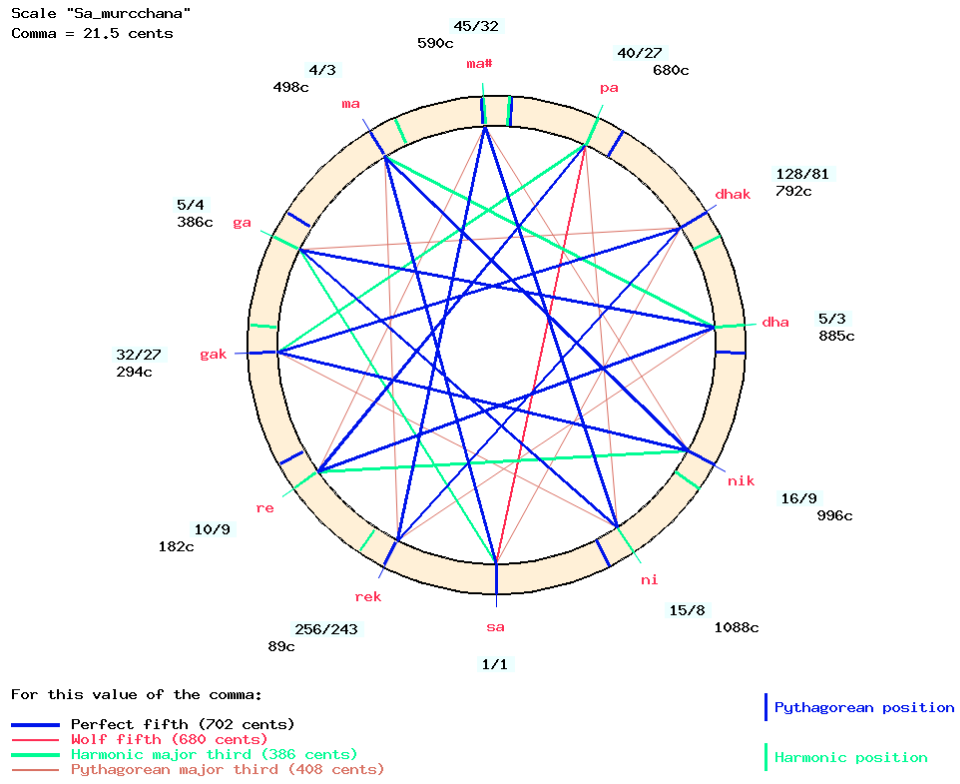
“Optimal con­so­nance” is illus­trat­ed by two fea­tures: 1) there is only one wolf’s fifth (red line) in the scale (between D and G), and 2) each note is con­nect­ed to every oth­er note by a per­fect fifth (blue line). This con­so­nance is of para­mount impor­tance to Indian musi­cians. Consonant inter­vals are casu­al­ly placed in melod­ic phras­es to enhance the “flavour” of their notes, and there should be no wolf’s fifth in the scale.

Note that the Ma-grama chro­mat­ic scale has all its notes in their low­er enhar­mon­ic positions.

The Ma-grama chro­mat­ic scale has been renamed “Sa_murcchana” here, because ‘S’ of the mov­ing wheel is oppo­site the ‘S’ of the fixed crown. The note names have been con­vert­ed (with a sin­gle click) to the Indian con­ven­tion. Note that the key num­bers have also been (auto­mat­i­cal­ly) fixed to match the exclu­sive­ly labelled notes. In this way, the upper “sa” is assigned key 72 instead of 83 in the “Ma01″ scale shown on the Just into­na­tion, a gen­er­al frame­work page. The tonal con­tent of this “Sa_murchana” is shown in this table:

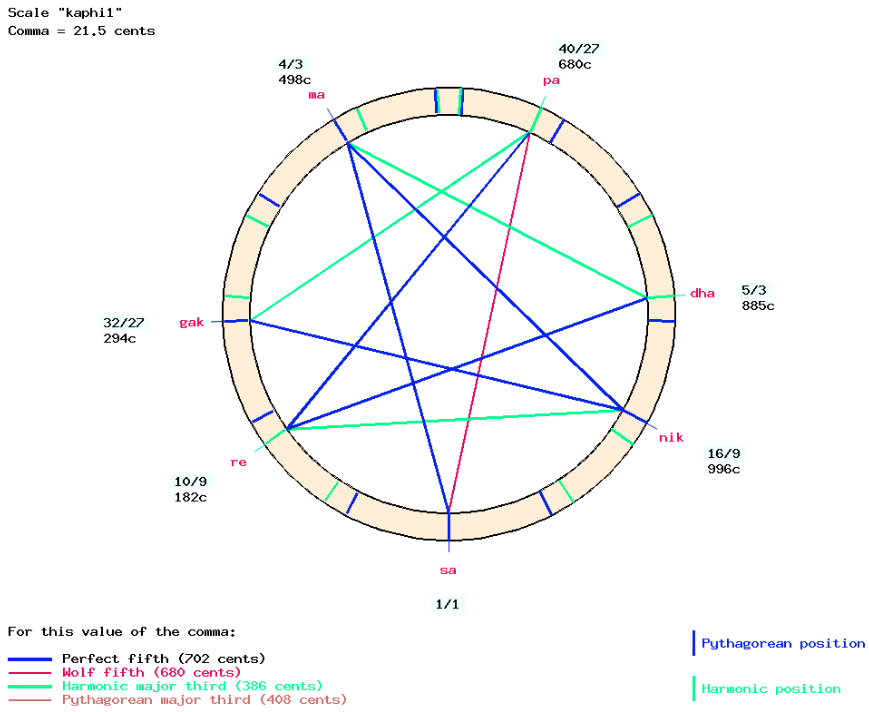
Selecting only “unal­tered” notes in “Sa_murcchana” — sa, re, gak, ma, pa, dha, nik — results in the “kaphi1″ scale type named after the raga Kaphi (pro­nounced ‘kafi’). This can be asso­ci­at­ed with a D-mode (Dorian) in west­ern musicology.

This scale type is saved under the name “kaphi1″ because there will be anoth­er ver­sion of the Kaphi scale type.

In “Sa_murcchana” the selec­tion of notes can be done in two dif­fer­ent ways:

• Select antara Gandhara (name­ly “ga”) in place of the scale’s Gandhara (name­ly “gak”), there­by rais­ing it by 2 shru­ti-s. This will result in a vikrit (mod­i­fied) scale type, name­ly “khamaj1″, asso­ci­at­ed with raga Khamaj.
• Select both antara Gandhara and kakali Nishada (name­ly “ni” in place of “nik” raised by 2 shru­ti-s) which cre­ates the “bilaval1″ scale type asso­ci­at­ed with raga Bilaval.

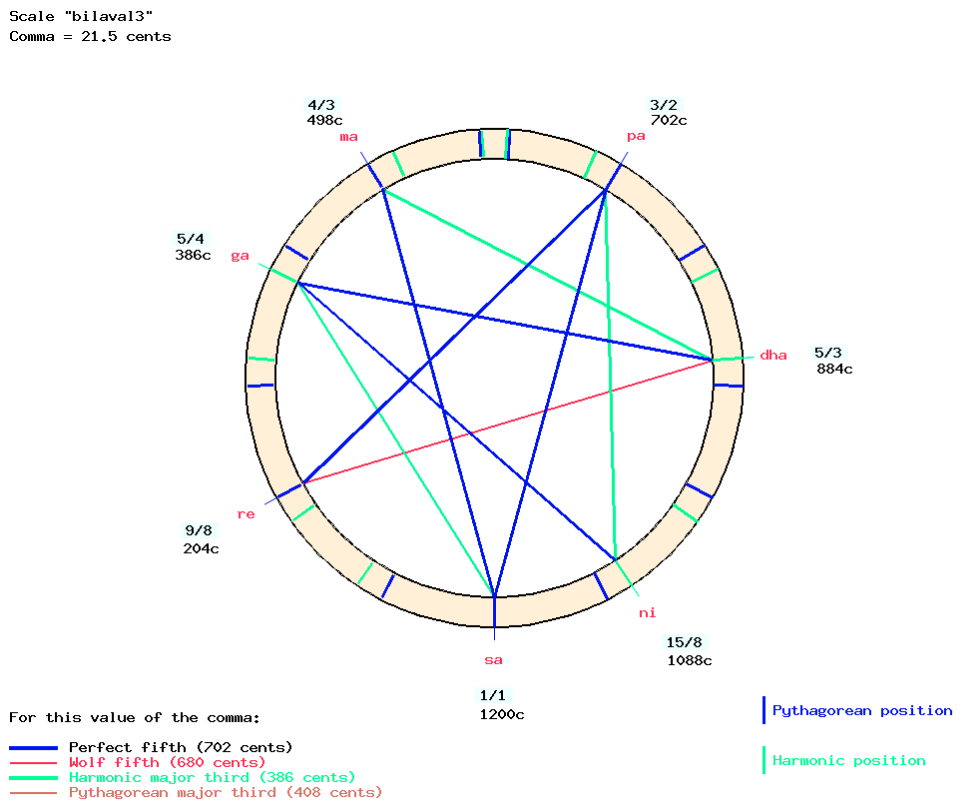
This “bilaval1″ scale type is one of three ver­sions of the Bilaval cre­at­ed by the mur­ccha­na process. Although it cor­re­sponds to the scale of the white keys on a key­board instru­ment, it is not the usu­al “just into­na­tion” dia­ton­ic scale, because of a wolf’s fifth between “sa” and “pa”.

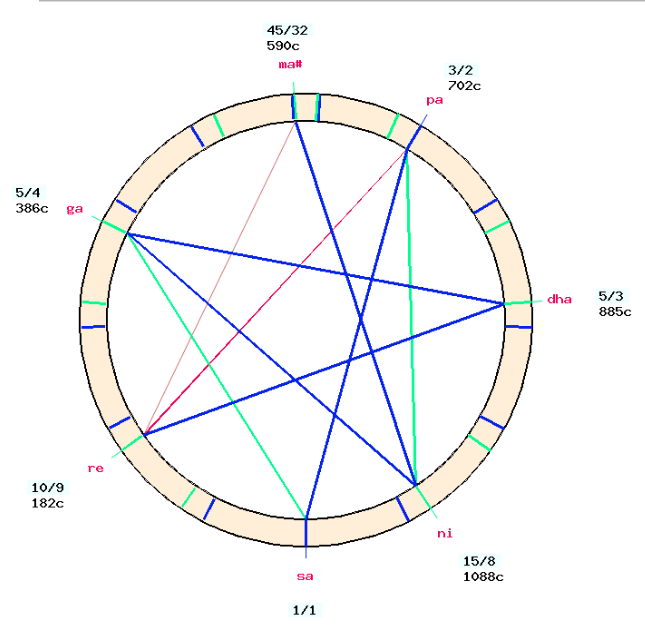
An alter­na­tive Bilaval scale type called “bilaval3″ (extract­ed from “Ni1_murcchana”, see below) cor­re­sponds to Giozeffo Zarlino’s “nat­ur­al” scale — see Just into­na­tion: a gen­er­al frame­work. This is not to be con­fused with Zarlino’s mean­tone tem­pera­ment dis­cussed on the Microtonality page.

A fourth option: rais­ing “nik” to “ni” and keep­ing “gak”, would pro­duce a scale type in which “ni” has no con­so­nant rela­tion­ship with any oth­er note in the scale. This option is there­fore dis­card­ed from the model.

Each mur­ccha­na of the Ma-grama chro­mat­ic scale pro­duces at least three types of scale by select­ing unal­tered notes, antara Gandhara or both antara Gandhara and kakali Nishada.

For exam­ple, to cre­ate “Ni1_murcchana”, open the “Sa_murcchana” page and enter “nik” (i.e. N3) as the note to be placed on “sa”.

Raga scale types are stored in the “-cs.raga” Csound resource file. Images are avail­able with a sin­gle click and scale struc­tures are com­pared on the main page.

The entire process is sum­ma­rized in the fol­low­ing table (Arnold 1982 p. 38):

Step	Ma-grama chro­mat­ic mur­ccha­na start­ing from	Shuddha gra­ma	Vikrit gra­ma (antara)	Vikrit gra­ma (antara + kakali)
1	Sa	kaphi1	khamaj1	bilaval1
2	Ma1	khamaj2	bilaval2	kalyan1
3	Ni1	bilaval3	kalyan2	marva1
4	Ga1	kalyan3	marva2	purvi1
5	Dha1	marva3	purvi2	todi1
6	Re1	purvi3	todi2
7	Ma3	todi3		lalit1 bhairao1
8	Ni3			lalit2 bhairao2 bhairavi1
9	Ga3			todi4 bhairavi2
10	Dha3		bhairavi3	asavari1
11	Re3	bhairavi4	asavari2	kaphi2
12	Pa3	asavari3	kaphi3	khamaj3

The use of this table deserves a graph­i­cal demon­stra­tion. For exam­ple, let us cre­ate a scale type “kalyan1″ based on the “Ma1_murcchana”. The table says that both “antara and kakali” should be select­ed. This means “antara Gandhara” which is “ga” in place of “gak” in the Ma-grama scale, and “kakali Nishada” which is “ni” in place of “nik” in the Ma-grama scale. This process is clear in the mov­ing wheel model:

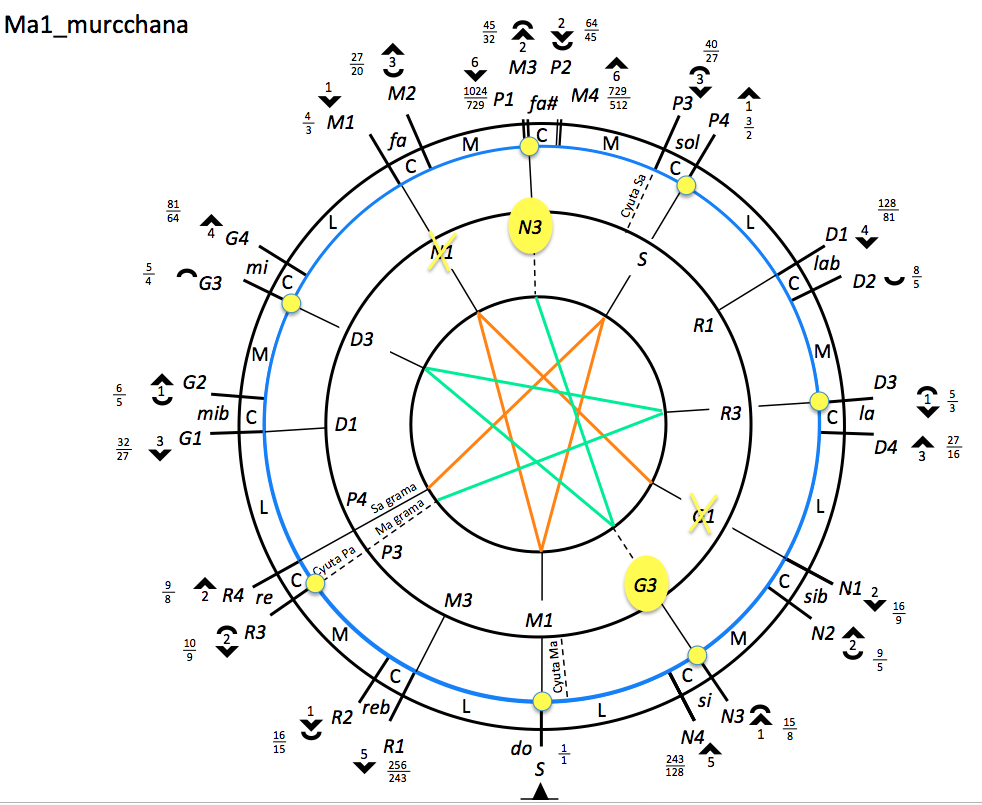
To make this selec­tion and export the “kalyan1″ scale type, fill in the form on the “Ma1_murcchana” page as shown in the image.

Below is the result­ing scale type.

Remember that note posi­tions expressed as whole-number fre­quen­cy ratios are only a mat­ter of con­ve­nience for read­ers famil­iar with west­ern musi­col­o­gy. It would be more appro­pri­ate to fol­low the Indian con­ven­tion of count­ing inter­vals in num­bers of shruti-s. In this exam­ple, the inter­val between ‘sa’ and ‘ma’ is increased from 9 shruti-s (per­fect fourth) to 11 shruti-s (tri­tone).

Arnold’s mod­el is an exten­sion of the mur­ccha­na sys­tem described in Natya Shastra because it accepts mur­ccha­na-s start­ing from notes that do not belong to the orig­i­nal (7-degree) Ma-grama, tak­en from its “chro­mat­ic ver­sion”: Dha1, Re1, Ma3, Ni3, Ga3. This exten­sion is nec­es­sary to cre­ate scale types for Todi, Lalit and Bhairao that include aug­ment­ed sec­onds.

In his 1982 paper (p. 39-41) Arnold linked his clas­si­fi­ca­tion of scale types to the tra­di­tion­al list of jāti-s, the “ances­tors of ragas” described in Sangita Ratnakara of Śārṅgadeva (Shringy & Sharma, 1978). Seven jāti-s are cit­ed (p. 41), each of them being derived from a mur­ccha­na of the Ma-grama on one of its shud­dha swara-s (basic notes).

Every jāti is asso­ci­at­ed with a note of relax­ation (nyasa swara). In con­tem­po­rary ragas, the nyasa swara is often found at the end of a phrase or a set of phras­es. In Arnold’s inter­pre­ta­tion, the same should define the mur­ccha­na from which the melod­ic type (jāti) is born. Since the names of the shud­dha jatis are in fact tied to their nyasa swaras, this also sug­gests that they should be tied to the mur­ccha­nas belong­ing to those nyasa swaras (Arnold 1982 p. 40).

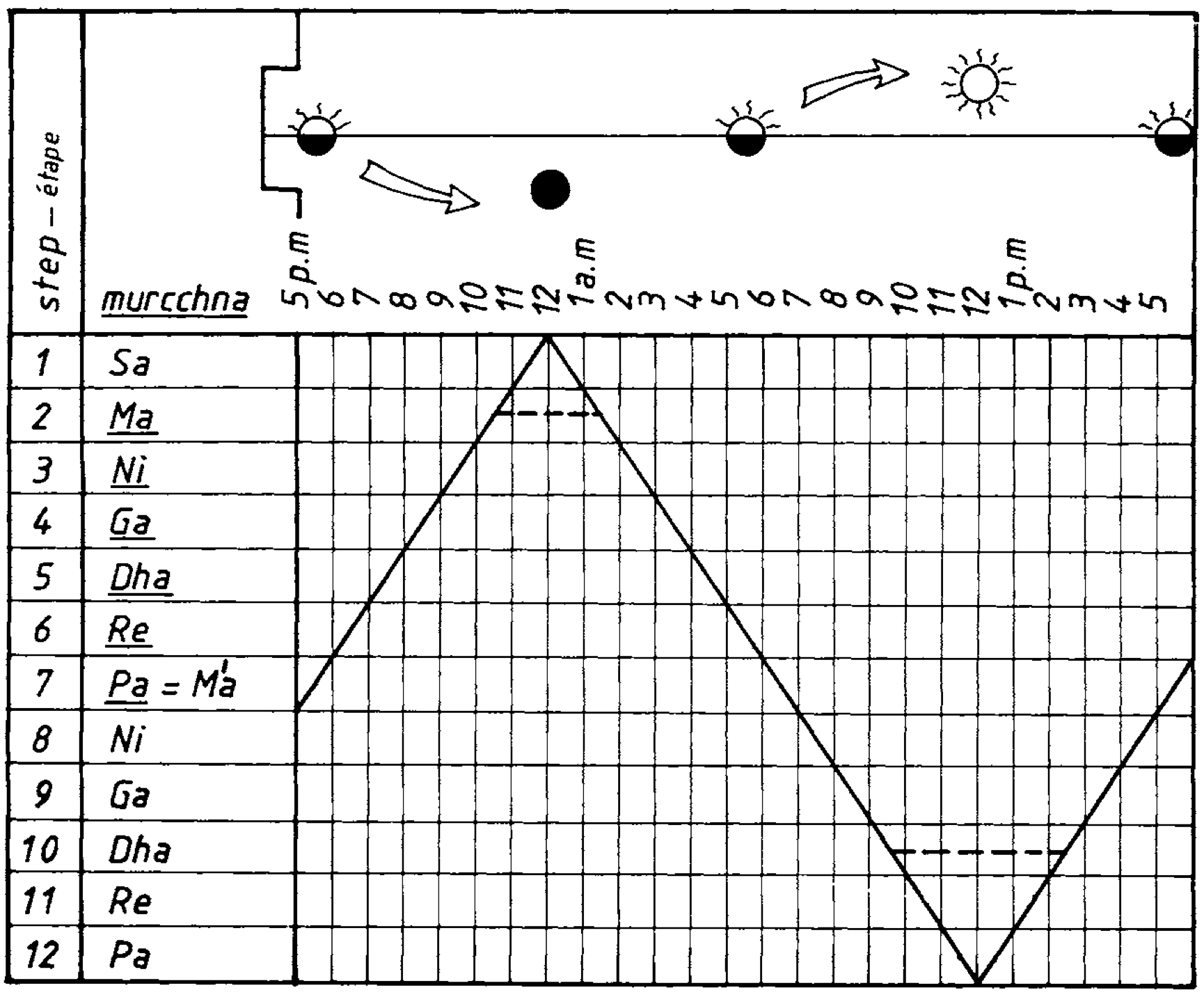
In oth­er pub­li­ca­tions (notably Arnold & Bel 1985), Arnold used the cycle of 12 chro­mat­ic scales to sug­gest that the enhar­mon­ic posi­tions of the notes could express states of ten­sion or release linked to the chang­ing ambi­ence of the cir­ca­di­an cycle, there­by pro­vid­ing an expla­na­tion for the per­for­mance times assigned to tra­di­tion­al ragas. Low enhar­mon­ic posi­tions would be asso­ci­at­ed with dark­ness and high­er ones with day­light. Thus, ragas con­struct­ed using the Sa mur­ccha­na of the Ma-grama chro­mat­ic scale (all low posi­tions, step 1) could be inter­pret­ed as being near mid­night, while those that mix low and high posi­tions (step 7) would car­ry the ten­sions of sun­rise and sun­set. Their sequence is a cycle because in the table above it is pos­si­ble to jump from step 12 to step 1 by low­er­ing all note posi­tions by one shru­ti. This cir­cu­lar­i­ty is implied by the process called sadja-sadharana in musi­co­log­i­cal lit­er­a­ture (Shringy & Sharma 1978).

A list of 85 ragas with per­for­mance times pre­dict­ed by the mod­el can be found in Arnold & Bel (1985). This hypoth­e­sis is indeed inter­est­ing — and it does hold for many well-known ragas — but we have nev­er found the time to under­take a sur­vey of musi­cians’ state­ments about per­for­mance times which might have assessed its validity.

Practice

Given scale types stored in the “-cs.raga” Csound resource file, Bol Processor + Csound can be used to check the valid­i­ty of scales by play­ing melodies of ragas they are sup­posed to embody. It is also inter­est­ing to use these scales in musi­cal gen­res unre­lat­ed with North Indian raga and “dis­tort” them in every con­ceiv­able direction…

Choice of a raga

We will take up the chal­lenge of match­ing one of the four “todi” scales with two real per­for­mances of raga Todi.

Miyan ki todi is present­ly the most impor­tant raga of the Todi fam­i­ly and there­fore often sim­ply referred to as Todi […], or some­times Shuddh Todi. Like Miyan ki mal­har it is sup­posed to be a cre­ation of Miyan Tansen (d. 1589). This is very unlike­ly, how­ev­er, since the scale of Todi at the time of Tansen was that of mod­ern Bhairavi (S R G M P D N), and the name Miyan ki todi first appears in 19^th cen­tu­ry lit­er­a­ture on music.

Joep Bor (1999)

This choice is chal­leng­ing for a num­ber of rea­sons. Firstly, the four vari­ants of “todi” scales are derived from a (ques­tion­able) exten­sion of the grama-murcchana sys­tem. Then, the notes “ni” and “rek”, “ma#” and “dhak” are close to the ton­ic “sa” and the dom­i­nant “pa” and could be “attract­ed” by the ton­ic and dom­i­nant, thus dis­rupt­ing the “geom­e­try” of the the­o­ret­i­cal scales in the pres­ence of a drone.

Finally, and most impor­tant­ly, the per­former’s style and per­son­al choic­es are expect­ed to be at odds with this the­o­ret­i­cal mod­el. As sug­gest­ed by Rao and van der Meer (2010, p. 693):

[…] it has been observed that musi­cians have their own views on into­na­tion, which are hand­ed down with­in the tra­di­tion. Most of them are not con­scious­ly aware of aca­d­e­m­ic tra­di­tions and hence are not in a posi­tion to express their ideas in terms of the­o­ret­i­cal for­mu­la­tions. However, their ideas are implic­it in musi­cal prac­tice as musi­cians visu­al­ize tones, per­haps not as fixed points to be ren­dered accu­rate­ly every time, but rather as tonal regions or pitch move­ments defined by the gram­mar of a spe­cif­ic raga and its melod­ic con­text. They also attach para­mount impor­tance to cer­tain raga-specific notes with­in phras­es to be intoned in a char­ac­ter­is­tic way.

We had already tak­en up the Todi chal­lenge with an analy­sis of eight occur­rences using the Melodic Movement Analyser (Bel 1988b). The analyser had pro­duced streams of accu­rate pitch mea­sure­ments which, after being fil­tered as selec­tive tona­grams, were sub­ject­ed to sta­tis­ti­cal analy­sis (Bel 1984; Bel & Bor 1984). The events includ­ed 6 per­for­mances of raga Todi and 2 exper­i­ments in tun­ing the Shruti Harmonium.

The MMA analy­sis revealed a rel­a­tive­ly high con­sis­ten­cy of note posi­tions, with stan­dard devi­a­tions bet­ter than 6 cents for all notes except “ma#”, for which the devi­a­tion rose to 10 cents, still an excel­lent sta­bil­i­ty. Comparison of these results with the ‘flex­i­ble’ grama-murcchana mod­el showed less than 4 cent stan­dard devi­a­tion of inter­vals for 4 dif­fer­ent scales in which the syn­ton­ic com­ma (pramāņa ṣru­ti) would be set at 6, 18, 5 and 5 cents respec­tive­ly. In dis­cussing tun­ing schemes, Wim van der Meer even sug­gest­ed that musi­cians could “solve the prob­lem” of a “ni-ma#” wolf’s fifth by tem­per­ing fifths over the “ni-ma#-rek-dhak” cycle (Bel 1988b p. 17).

Our con­clu­sion was that no par­tic­u­lar “tun­ing scheme” could be tak­en for grant­ed on the basis of “raw” data. It would be more real­is­tic to study a par­tic­u­lar per­for­mance by a par­tic­u­lar musician.

Choice of a musician

Working with the Shruti Harmonium nat­u­ral­ly led us to meet Kishori Amonkar (1932-2017) in 1981. She was a lead­ing expo­nent of Hindustani music, hav­ing devel­oped a per­son­al style that claimed to tran­scend clas­si­cal schools (gha­ranas).

Most inter­est­ing­ly, she per­formed accom­pa­nied by a swara man­dal (see pic­ture), a zither that she tuned for each raga. Unfortunately we were not equipped to mea­sure these tun­ings with suf­fi­cient accu­ra­cy. So we used the Shruti Harmonium to pro­gramme the inter­vals accord­ing to her instructions.

This exper­i­ment did not go well for two rea­sons. A tech­ni­cal one: on that day, a fre­quen­cy divider (LSI cir­cuit) on the har­mo­ni­um was defec­tive; until it was replaced, some pro­grammed inter­vals were inac­ces­si­ble. A musi­cal one: the exper­i­ment showed that this pre­cise har­mo­ni­um was not suit­able for tun­ing exper­i­ments with Indian musi­cians. The fre­quen­cy ratios had to be entered on a small key­board, a use too far removed from the prac­tice of string tun­ing. This was a major incen­tive to design and build our “micro­scope for Indian music”, the Melodic Movement Analyser (MMA) (Bel & Bor 1984).

In the fol­low­ing years (1981-1984) MMA exper­i­ments took up all our time and revealed the vari­abil­i­ty (but not the ran­dom­ness) of raga into­na­tion. For this rea­son we could not return to tun­ing exper­i­ments. Today, a sim­i­lar approach would be much eas­i­er with the help of the Bol Processor BP3… if only the expert musi­cians of that time were still alive!

Choice of a scale type

We need to decide between the four “todi” scale types pro­duced by the mur­ccha­na-s of the Ma-grama chro­mat­ic scale. For this we can use the mea­sure­ments of the Melodic Movement Analyser (Bel 1988b p. 15). Let us take aver­age mea­sure­ments and those of a per­for­mance by Kishori Amonkar. These are note posi­tions (in cents) against the ton­ic “sa”.

Note	Average	Standard devi­a­tion	Kishori Amonkar
rek	95	4	96
gak	294	4	288
ma#	606	10	594
pa	702	1	702
dhak	792	3	792
(dhak)	806	3	810
ni	1107	6	1110

For the moment we will ignore “dhak” in the low­er octave as it will be dealt with sep­a­rate­ly. Let us com­pare Kishori Amonkar’s results with the four scale types:

Note	Kishori Amonkar	todi1	todi2	todi3	todi4
rek	96	89	89	89	112
gak	288	294	294	294	294
ma#	594	590	590	610	610
pa	702	702	702	700	702
dhak	792	792	792	792	814
ni	1110	1088	1109	1109	1109

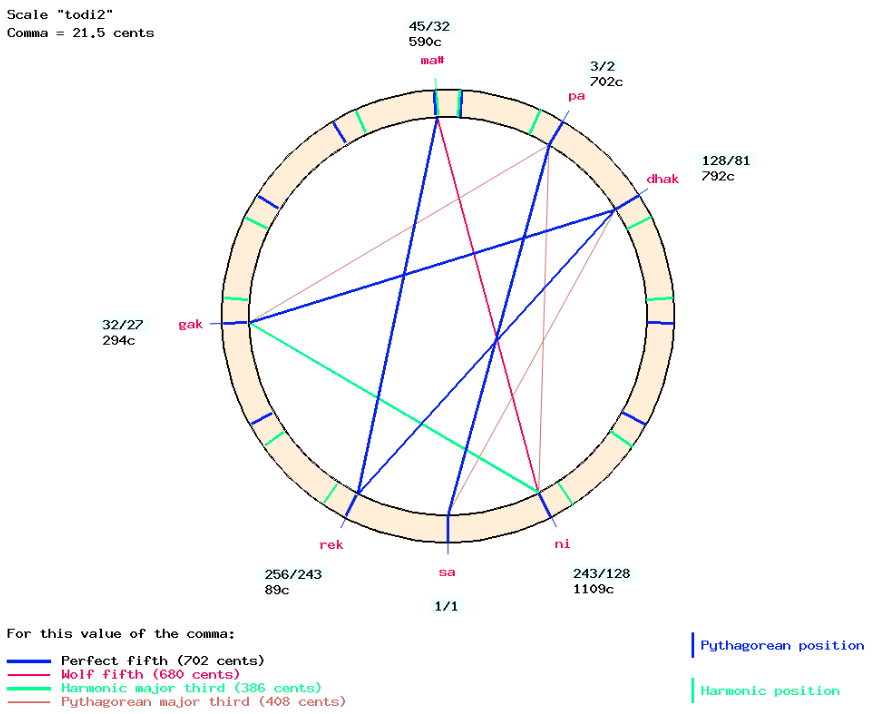
There are sev­er­al ways of find­ing the best match for musi­cal scales: either by com­par­ing scale inter­vals or by com­par­ing note posi­tions in rela­tion to the base note (ton­ic). Because of the impor­tance of the drone, we will use the sec­ond method. The choice is sim­ple here. Version “todi1″ can be dis­card­ed because of “ni”, the same with “todi3″ and “todi4″ because of “ma#”. We are left with “todi2″ which has a very good match, even with the mea­sure­ments of per­for­mances by oth­er musicians.

Adjustment of the scale

The largest devi­a­tions are on “rek” which was sung 7 cents high­er than the pre­dict­ed val­ue and “gak” which was sung 6 cents low­er. Even a 10-cent devi­a­tion is prac­ti­cal­ly impos­si­ble to mea­sure on a sin­gle note sung by a human, includ­ing a high-profile singer like Kishori Amonkar; the best res­o­lu­tion used in speech prosody is greater than 12 cents.

Any “mea­sure­ment” of the MMA is an aver­age of val­ues along the rare sta­ble melod­ic steps. It may not be rep­re­sen­ta­tive of the “real” note due to its depen­dence on note treat­ment: if the note’s approach is in a range on the lower/higher side, the aver­age will be lower/higher than the tar­get pitch.

Therefore, it would be accept­able to declare that the scale type “todi2″ cor­re­sponds to the per­for­mance. However, let us show how the mod­el can be mod­i­fied to reflect the mea­sure­ments more accurately.

First we dupli­cate “todi2″ to cre­ate “todi-ka” (see pic­ture). Note posi­tions are iden­ti­cal in both versions.

Looking at the pic­ture of the scale (or the num­bers on its table), we can see that all the note posi­tions except “ma#” are Pythagorean. The series to which a note belongs is indi­cat­ed by the colour of its point­er: blue for Pythagorean and green for harmonic.

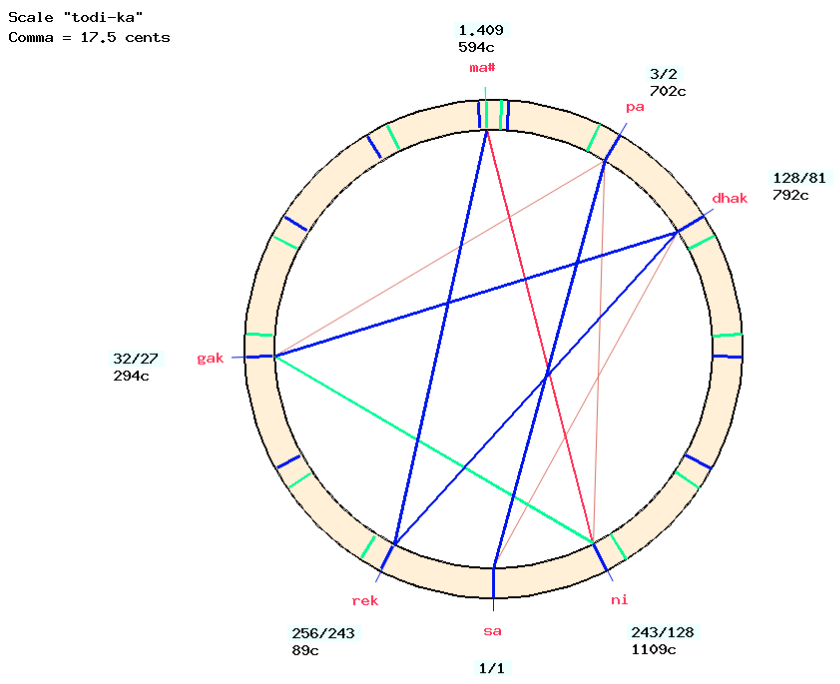
This means that chang­ing the size of the syn­ton­ic com­ma — in strict accor­dance with the grama-murcchana mod­el — will only adjust “ma#”. To change the posi­tion of “ma#” from 590 to 594 cents (admit­ted­ly a ridicu­lous adjust­ment) we need to reduce the size of the syn­ton­ic com­ma by the same amount. This can be done at the bot­tom right of the “todi-ka” page, chang­ing the syn­ton­ic com­ma to 17.5 cents, a change con­firmed by the new image.

A table on the “todi-ka” page shows that the “rek-ma#” inter­val is still con­sid­ered a “per­fect” fifth, even though it is small­er by 6 cents.

It may not be obvi­ous whether the syn­ton­ic com­ma needs to be increased or decreased to fix the posi­tion of “ma#”, but it is easy to try the oth­er way in case the direc­tion was wrong.

Other adjust­ments devi­ate from the “pure” mod­el. These result in chang­ing fre­quen­cy ratios in the table on the “todi-ka” page. An increase in “rek” from 89 to 96 cents requires an increase of 7 cents, cor­re­spond­ing to a ratio of 2(7/1200) = 1.00405. This changes the posi­tion of “rek” from 1.053 to 1.057.

In the same way, a reduc­tion in “gak” from 294 to 288 cents requires a reduc­tion of 6 cents, giv­ing a ratio of 2^(-6/1200) = 0.9965. This brings the posi­tion of “gak” from 1.185 to 1.181.

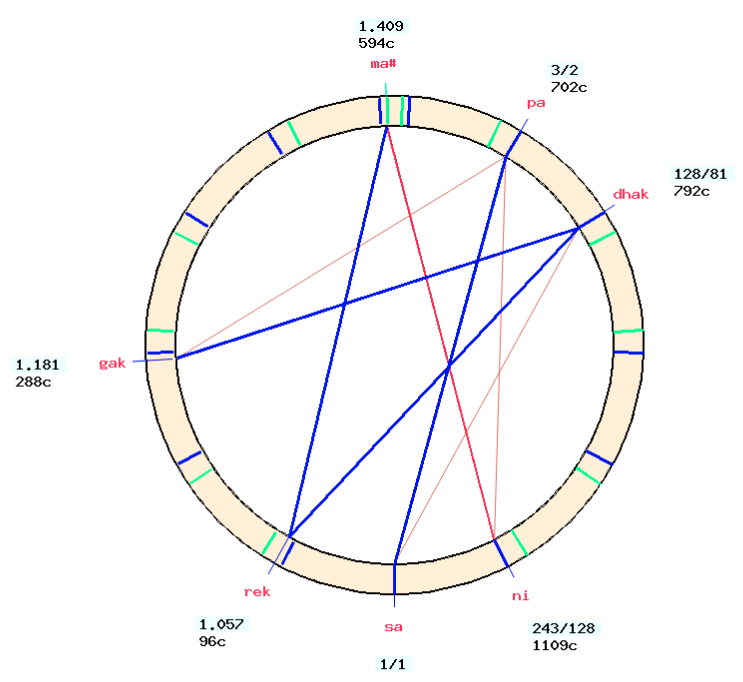
Fortunately, these cal­cu­la­tions are done by the machine: use the “MODIFY NOTE” but­ton on the scale page.

The pic­ture shows that the infor­ma­tion of “rek” and “gak” belong­ing to Pythagorean series (blue line) is pre­served. The rea­son for this is that when­ev­er a fre­quen­cy ratio is mod­i­fied by its floating-point val­ue, the machine checks whether the new val­ue is close to an inte­ger ratio of the same series. For exam­ple, chang­ing “rek” back to 1.053 would restore its ratio to 256/243. Accuracy bet­ter than 1‰ is required for this adjustment.

A tun­ing scheme for this scale type is sug­gest­ed by the machine. The graph­i­cal rep­re­sen­ta­tion shows that “ni” is not con­so­nant with “ma#” as their inter­val is 684 cents, close to a wolf’s fifth of 680 cents. Other notes are arranged on two cycles of per­fect fifths. Interestingly, rais­ing “rek” by 7 cents brought the “rek-ma#” fifth back to its per­fect size (702 cents).

Again, these are mean­ing­less adjust­ments for a vocal per­for­mance. We are just show­ing what to do when necessary.

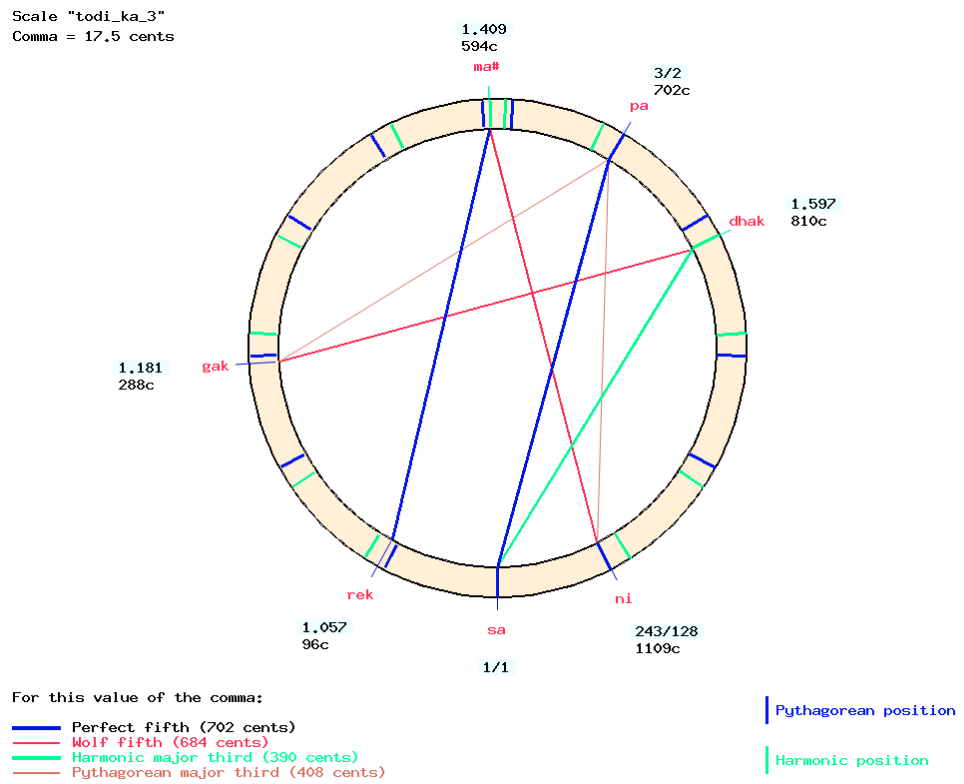
The remain­ing adjust­ment will be that of the “dhak” in the low­er octave. To do this, we will dupli­cate the pre­vi­ous scale, renam­ing it “todi_ka_4″ to indi­cate that it is designed for the 4^th octave. In the new scale, called “todi_ka_3″, we raise “dhak3” by 810 -792 = 18 cents.

This rais­es its posi­tion from 1.58 to 1.597. Note that this puts it exact­ly in a posi­tion in the har­mon­ic series since the syn­ton­ic com­ma is 17.5 cents.

In addi­tion, “dhak-sa” is now a har­mon­ic major third — with a size of 390 cents to match the 17.5 cents com­ma. This is cer­tain­ly sig­nif­i­cant in the melod­ic con­text of this raga, which is one rea­son why all the musi­cians made the same size adjust­ment in their tun­ing experiments.

This case is a sim­ple illus­tra­tion of raga into­na­tion as a trade-off between har­monic­i­ty with respect to the drone and the need for con­so­nant melod­ic inter­vals. It also shows that the Shruti Harmonium could not fol­low the prac­tice of the musi­cians because its scale ratios were repli­cat­ed in all octaves.

Choice of a recording

We don’t have the record­ing on which the MMA analy­sis was made. One prob­lem with old tape record­ings is the unre­li­a­bil­i­ty of the speed of tape trans­port. Also, on a long record­ing, the fre­quen­cy of the ton­ic can change slight­ly due to vari­a­tions in room tem­per­a­ture, which affects the instru­ments — includ­ing the dila­tion of the tape…

In order to try to com­pare scales a with real per­for­mances, and to exam­ine extreme­ly small “devi­a­tions” (which have lit­tle musi­cal sig­nif­i­cance, in any case), it is there­fore safer to work with dig­i­tal record­ings. This was the case with Kishori Amonkar’s Todi, record­ed in London in ear­ly 2000 for the Passage to India col­lec­tion, and avail­able free of copy­right (link on Youtube). The fol­low­ing is based on this recording.

Setting up the diapason

Let us cre­ate the fol­low­ing “-gr.tryRagas” gram­mar:

-se.tryRagas
-cs.raga

S --> _scale(todi_ka_4,0) sa4

In “-se.tryRagas” the note con­ven­tion should be set to “Indian” so that “sa4” etc. is accept­ed even when no scale is specified.

The gram­mar calls “-cs.raga”, which con­tains the def­i­n­i­tions of all the scale types cre­at­ed by the pro­ce­dure described above. Unsurprisingly, it does not play the note “sa” at the fre­quen­cy of the record­ing. We there­fore need to mea­sure the ton­ic in order to adjust the fre­quen­cy of “A4” (dia­pa­son) in “-se.tryRagas” accord­ing­ly. There are sev­er­al ways to do this with increas­ing accuracy.

A semi­tone approx­i­ma­tion can be obtained by com­par­ing the record­ing with notes played on a piano or any elec­tron­ic instru­ment tuned with A4 = 440 Hz. Once we have found the key that is clos­est to “sa” we cal­cu­late its fre­quen­cy ratio to A4. If the key is F#4, which is 3 semi­tones low­er than A4, the ratio is r = 2^(-3/12) = 0.840. To get this fre­quen­cy on “sa4” we would there­fore have to adjust the fre­quen­cy of the dia­pa­son (in “-se.tryRagas”) to:

440 * r * 2^(9/12) = 440 * 2^((9-3)/12) = 311 Hz

A much bet­ter approx­i­ma­tion is obtained by extract­ing a short occur­rence of “sa4” at the very begin­ning of the performance:

Then select a seem­ing­ly sta­ble seg­ment and extend the time scale to get a vis­i­ble signal:

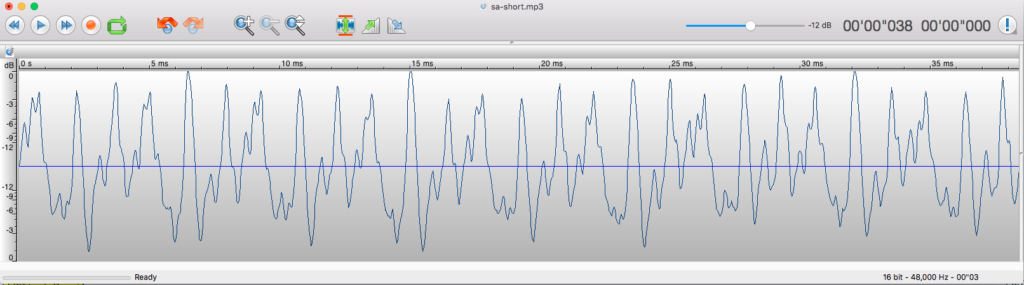
This sam­ple con­tains 9 cycles for a dura­tion of 38.5 ms. The fun­da­men­tal fre­quen­cy is there­fore 9 * 1000 / 38.5 = 233.7 Hz. Consequently, adjust the dia­pa­son in “-se.tryRagas” to 233.7 * 2^(9/12) = 393 Hz.

The last step is a fine tun­ing by com­par­ing the pro­duc­tion of the notes in the gram­mar by ear with the record­ing of “sa4” played in a loop. To do this, we pro­duce the fol­low­ing sequence:

S --> _pitchrange(500) _tempo(0.2) Scale _pitchbend(-15) sa4 _pitchbend(-10) sa4 _pitchbend(-5) sa4 _pitchbend(-0) sa4 _pitchbend(+5) sa4 _pitchbend(+10) sa4 _pitchbend(+15) sa4 _pitchbend(+20) sa4

These are eight occur­rences of “sa4” played at slight­ly increas­ing pitch­es adjust­ed by the pitch­bend. First make sure that the pitch­bend is mea­sured in cents: this is spec­i­fied in the instru­ment “Vina” called by “-cs.raga” and the Csound orches­tra file “new-vina.orc”.

Listening to the sequence may not reveal any pitch dif­fer­ences, but these will be appar­ent to a trained ear when super­im­posed on the recording:

One of the four occur­rences sounds best in tune. Let us assume that the best match is on _pitchbend(+10). This means that the dia­pa­son should be raised by 10 cents. Its new fre­quen­cy would there­fore be 393 * 2^(10/1200) = 395.27 Hz.

In fact the best fre­quen­cy is 393.22 Hz, which means that the sec­ond eval­u­a­tion (which gave 393 Hz) was fair — and the singers’ voic­es very reli­able! Now we can check the fre­quen­cy of “sa4” on the Csound score:

; Csound score
f1 0 256 10 1 ; This table may be changed
t 0.000 60.000
i1 0.000 5.000 233.814 90.000 90.000 0.000 -15.000 -15.000 0.000 ; sa4
i1 5.000 5.000 233.814 90.000 90.000 0.000 -10.000 -10.000 0.000 ; sa4
i1 10.000 5.000 233.814 90.000 90.000 0.000 -5.000 -5.000 0.000 ; sa4
i1 15.000 5.000 233.814 90.000 90.000 0.000 0.000 0.000 0.000 ; sa4
i1 20.000 5.000 233.814 90.000 90.000 0.000 5.000 5.000 0.000 ; sa4
i1 25.000 5.000 233.814 90.000 90.000 0.000 10.000 10.000 0.000 ; sa4
i1 30.000 5.000 233.814 90.000 90.000 0.000 15.000 15.000 0.000 ; sa4
i1 35.000 5.000 233.814 90.000 90.000 0.000 20.000 20.000 0.000 ; sa4
s

These meth­ods could actu­al­ly be sum­marised by the third: use the gram­mar to pro­duce a sequence of notes in a wide range to deter­mine an approx­i­mate pitch of “sa4” until the small range for the pitch­bend (± 200 cents) is reached. Then play sequences with pitch­bend val­ues in increas­ing accu­ra­cy until no dis­crim­i­na­tion is possible.

In a real exer­cise it would be safe to check the mea­sure­ment of “sa4” against occur­rences in sev­er­al parts of the recording.

This approach is too demand­ing in terms of accu­ra­cy for the analy­sis of a vocal per­for­mance, but it will be notice­able when work­ing with a long-stringed instru­ment such as the rudra veena. We will demon­strate this with Asad Ali Kan’s per­for­mance.

Matching phrases of the performance

We are now ready to check whether note sequences pro­duced by the mod­el would match sim­i­lar sequences in the recording.

First we try a sequence with the empha­sis on “rek”. The fol­low­ing sequence of notes is pro­duced by the grammar:

S --> KishoriAmonkar1
KishoriAmonkar1 --> Scale _ {2, dhak3 sa4 ni3 sa4} {7, rek4} _ {2, dhak3 sa4 ni3 dhak3} {2, dhak3 _ ni3 sa4} {5, rek4}
Scale --> _scale(todi_ka_3,0)

Below is the phrase sung by the musi­cians (posi­tion 0′50″) then repeat­ed in super­posed form with the sequence pro­duced by the grammar:

In this exam­ple, the scale “todi_ka_3″ has been used because of the occur­rence of short instances of “dhak3”. The posi­tion of “rek” is iden­ti­cal in the 3^d and 4^th octaves. The blend­ing of the voice with the plucked instru­ment is notable in the last held note.

In the next sequence (loca­tion 1′36″) the posi­tion of “gak4” is esti­mat­ed. The gram­mar is as follows:

S --> KishoriAmonkar2
KishoriAmonkar2 --> Scale {137/100, sa4 rek4 gak4 rek4} {31/10, rek4} {18/10, gak4} {75/100,rek4} {44/10, sa4}
Scale --> _scale(todi_ka_4,0)

This time, the scale “todi_ka_4″ was cho­sen, even though it had no effect on the into­na­tion since “dhak” is missing.

A word about build­ing the gram­mar: we looked at the sig­nal of the record­ed phrase and mea­sured the (approx­i­mate) dura­tion of the notes: 1.37s, 3.1s, 1.8s, 7.5s, 4.4s. We then con­vert­ed these dura­tions into inte­ger ratios — frac­tions of the basic tem­po whose peri­od is exact­ly 1 sec­ond, as spec­i­fied in “-se.tryRagas”: 137/100, 31/10 etc.

Below is a pianoroll of the sequence pro­duced by the grammar:

No we try a phrase with a long pause on “dhak3” (loca­tion 3′34″), which proves that the scale “todi_ka_3″ per­fect­ly match­es this occur­rence of “dhak”:

S --> KishoriAmonkar3
KishoriAmonkar3 --> scale(todi_ka_3,0) 11/10 {19/20, ma#3 pa3} {66/10,dhak3} {24/10, ni3 dhak3 pa3 }{27/10,dhak3} 12/10 {48/100,dhak3}{17/10,ni3}{49/10,dhak3}

Early occur­rence of “ma#4” (loca­tion 11′38″):

S --> KishoriAmonkar4
KishoriAmonkar4 --> _scale(todi_ka_4,0) 4/10 {17/10, ni3}{26/100,sa4}{75/100,rek4}{22/100,gak4}{17/10,ma#4}{16/100,gak4}{34/100,rek4}{56/100,sa4}{12/100,rek4}{84/100,gak4}{27/100,rek4}{12/10,sa4}

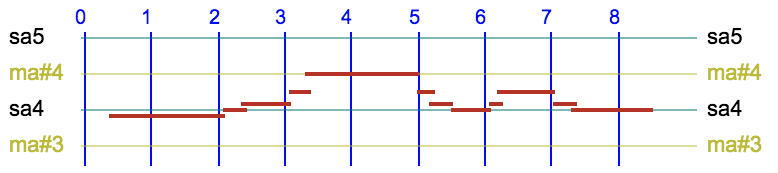
Reaching “dhak4” (loca­tion 19′46″):

S --> KishoriAmonkar5
KishoriAmonkar5 --> _scale(todi_ka_4,0) 13/10 {16/10,ma#4}{13/10,gak4}{41/100,ma#4}{72/100,ma#4 dhak4 ma#4 gak4 ma#4}{18/10,dhak4}{63/100,sa4}{90/100,rek4}{30/100,gak4}{60/100,rek4}{25/100,sa4}{3/2,rek4}

With a light touch of “pa4” (loca­tion 23′11″):

S --> KishoriAmonkar6
KishoriAmonkar6 --> _scale(todi_ka_4,0) 28/100 {29/100,ma#4}{40/100,dhak4}{63/100,ni4 sa5 ni4}{122/100,dhak4}{64/100,pa4}{83/100,ma#4}{44/100,pa4}{79/100,dhak4}

Pitch accu­ra­cy is no sur­prise in Kishori Amonkar’s per­for­mances. With a keen aware­ness of “shru­ti-s”, she would sit on the stage and pluck her swara man­dal, care­ful­ly tuned for each raga.

A test with the rudra veena

Asad Ali Khan (1937-2011) was one of the last per­form­ers of the rudra veena at the end of the 20^th cen­tu­ry and a very sup­port­ive par­tic­i­pant in our sci­en­tif­ic research on raga intonation.

➡ An out­stand­ing pre­sen­ta­tion of Asad Ali Khan and his idea of music is avail­able in a film by Renuka George.

Pitch accu­ra­cy on this instru­ment is such that we have been able to iden­ti­fy tiny vari­a­tions that are con­trolled and sig­nif­i­cant in the con­text of the raga. See for exam­ple Playing with Intonation (Arnold 1985). To mea­sure vibra­tions below the audi­ble range, we occa­sion­al­ly placed a mag­net­ic pick­up near the last string.

Below are the sta­tis­tics of the Melodic Movement Analyser mea­sure­ments of the raga Miyan ki Todi inter­pret­ed by Asad Ali Khan in 1981. The sec­ond col­umn con­tains mea­sure­ments of his tun­ing of the Shruti Harmonium dur­ing an exper­i­ment. The columns on the right show the pre­dict­ed note posi­tions accord­ing to the grama-murchana mod­el with a syn­ton­ic com­ma of ratio 81/80. As shown in Kishori Amonkar’s per­for­mance above, “dhak” can take dif­fer­ent val­ues depend­ing on the octave.

Note	Asad Ali Khan per­form­ing	Asad Ali Khan tun­ing	todi1	todi2	todi3	todi4
rek	99	100	89	89	89	112
gak	290	294	294	294	294	294
ma#	593	606	590	590	610	610
pa	702	702	702	702	700	702
dhak3	795	794	792	792	792	814
dhak2	802
ni	1105	1108	1088	1109	1109	1109

Again, the best match would be the “todi2″ scale with a syn­ton­ic com­ma of 17.5 cents. We cre­at­ed two scales, “todi_aak_2″ and “todi_aak_3″ for the 2^nd and 3^rd octaves.

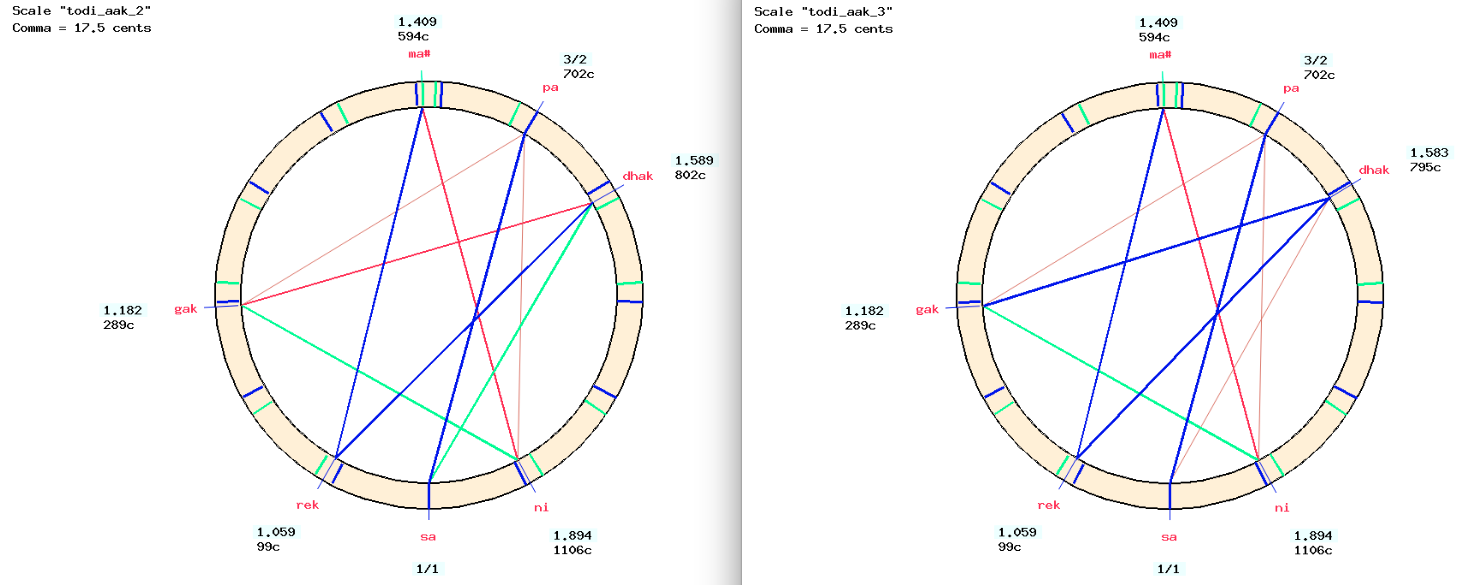
The scale con­struct­ed dur­ing the Shruti Harmonium exper­i­ment is less rel­e­vant because of the influ­ence of the exper­i­menter play­ing the scale inter­vals with a low-attracting drone (pro­duced by the machine). In his attempt to resolve the dis­so­nance in the scale — which always con­tained a wolf’s fifth and sev­er­al Pythagorean major thirds — Khan saheb end­ed up with a tun­ing iden­ti­cal to the ini­tial one, but one com­ma low­er. This was not a musi­cal­ly sig­nif­i­cant situation!

The scale “todi_aak_2″ (in the low octave) con­tains inter­est­ing inter­vals (har­mon­ic major thirds) which allows us to antic­i­pate effec­tive melod­ic move­ments. The tun­ing scheme sum­maris­es these relationships.

We now take frag­ments of Asad Ali Khan’s per­for­mance of Todi (2005) avail­able on Youtube (fol­low this link).

The per­for­mance begins in the low­er octave, so with the scale “todi_aak_2″. The fre­quen­cy of Sa was mea­sured at 564.5 Hz using the method described above.

Let us start with a sim­ple melod­ic phrase repeat­ed twice, the sec­ond time super­im­posed on the note sequence pro­duced by the grammar.

S --> AsadAliKhan1
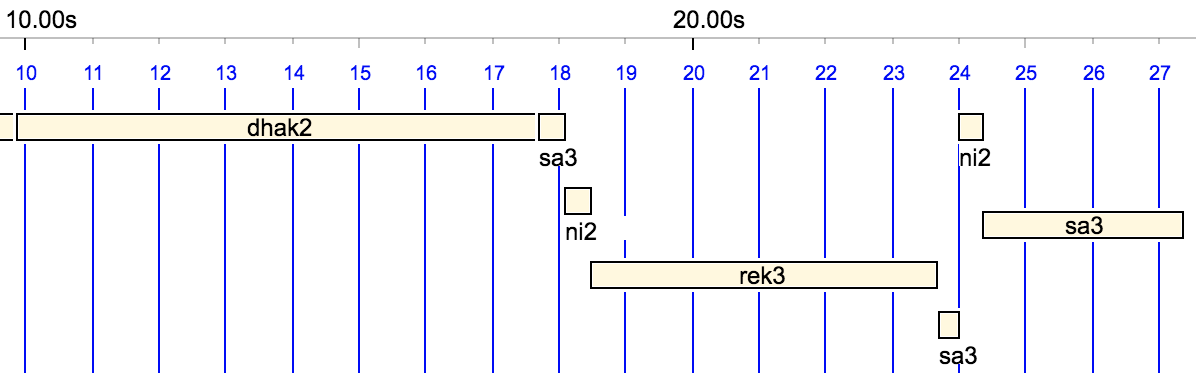
AsadAliKhan1 --> _scale(todi_aak_2,0) 45/100 {69/10,sa3} {256/100,dhak2} {78/10,dhak2} {12/10,sa3 ni2 rek3&} {48/10,&rek3} {98/100,sa3 ni2 sa3&} {27/10,&sa3}

This gram­mar con­tains an unusu­al char­ac­ter ‘&’, which is used to con­cate­nate sound objects (or notes) across the bound­aries of poly­met­ric expres­sions (between curly brack­ets). This makes it pos­si­ble to play the final “rek3” and “sa3” as con­tin­u­ous notes. This con­ti­nu­ity can be seen in the graph below:

It is time to make sure that fine tun­ing and adjust­ing scales are more than just an intel­lec­tu­al exer­cise… After all, the main dif­fer­ence between scales “todi_aak_2″ and “todi_aak_3″ is that “dhak” is 7 cents high­er in “todi_aak_2″, which means a third of a com­ma! To check the effect of the fine-tuning, lis­ten to the over­lay twice, once with “todi_aak_3″ and the sec­ond time with “todi_aak_2″:

To check the dif­fer­ence between these two ver­sions of “dhak2”, we can play them one after the oth­er and then super­im­pose them:

S --> _tempo(1/2) _scale(todi_aak_3,0) dhak2 _scale(todi_aak_2,0) dhak2 {_scale(todi_aak_3,0) dhak2, _scale(todi_aak_2,0) dhak2}

With fun­da­men­tal fre­quen­cies of 132.837 Hz and 133.341 Hz, the beat fre­quen­cy (of the sine waves) would be 133.341 - 132.837 = 0.5 Hz. The per­ceived beat fre­quen­cy is high­er because of the inter­fer­ence between the high­er par­tials. This sug­gests that a dif­fer­ence of 7 cents is not irrel­e­vant in the con­text of notes played by a long-stringed instru­ment (Arnold 1985).

More in the low­er octave:

S --> AsadAliKhan2
AsadAliKhan2 --> scale(todi_aak_2,0) _volume(64) _pitchrange(500) _pitchcont 93/100 {81/10,pa2}{38/10,pa2 gak2 pa2 dhak2 pa2 }{19/10,gak2}{43/10, _pitchbend(0) rek2 _pitchbend(-100) rek2&} _volumecont _volume(64) {2, _pitchbend(-100) &rek2} _volume(0) _volume(64) {23/10,ni2__ dhak2}{103/100,sa3&}{4,&sa3} 15/10 _volume(64) {38/10,sa3} _volume(0)

As “sa2” is out­side the range of the Csound instru­ment “Vina”, it is played here as “rek2” with a pitch­bend cor­rec­tion of one semitone.

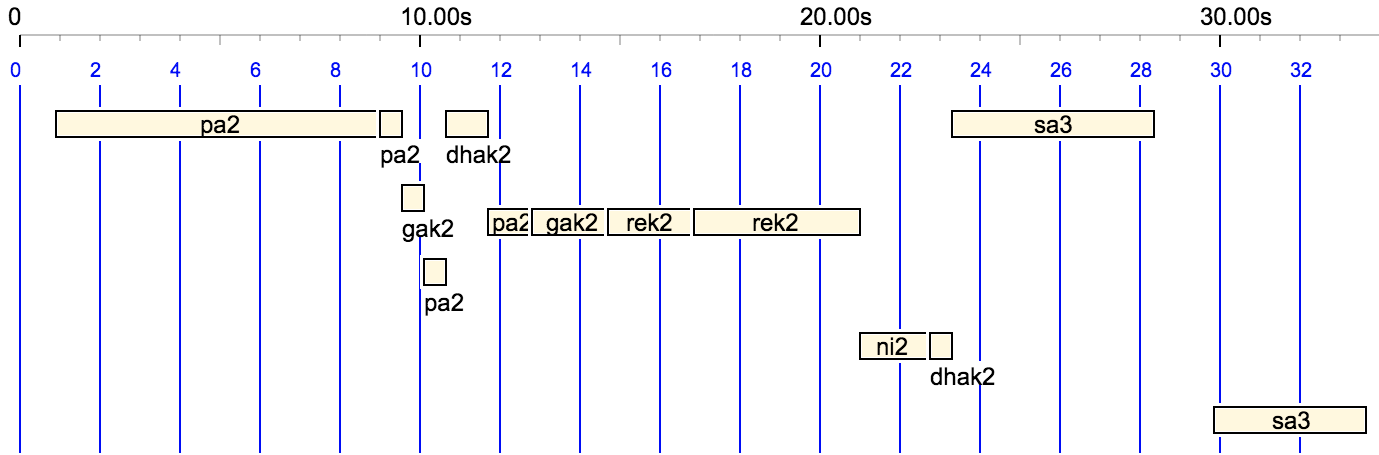
The ren­der­ing of phras­es in the low­er octave is very approx­i­mate because of the pre­dom­i­nance of meend (pulling the string). Some effects can be bet­ter imi­tat­ed using per­for­mance con­trols — see Sarasvati Vina, for exam­ple — but this requires a mas­tery of the real instru­ment in order to design pat­terns of musi­cal “ges­tures” rather than sequences of sound events… Imitating the melod­ic intri­ca­cy of a raga is not the sub­ject of this page; we are mere­ly check­ing the rel­e­vance of scale mod­els to the “tonal skele­ton” of ragas.

Accidental notes

Raga scales extract­ed from mur­chana-s of the Ma-grama chro­mat­ic scale (see above) con­tain only notes that are pre­sumed to belong to the raga. They can­not accom­mo­date acci­den­tal notes or the scales used in the com­mon prac­tice of mix­ing ragas.

Let us take, for exam­ple, a frag­ment of the pre­vi­ous exam­ple, which was poor­ly rep­re­sent­ed by the sequence of notes pro­duced by the gram­mar. (We learn from our mis­takes!) We might be tempt­ed to replace the expres­sion {38/10, pa2 gak2 pa2 dhak2 _ pa2 _} with {38/10, pa2 ga2 pa2 dhak2 _ pa2 _}, using “ga2” which does not belong to the scale “todi_aak_2″. Unfortunately, this results in an error message:

ERROR Pitch class ‘4’ does not exist in _scale(todi_aak_2). No Csound score produced.

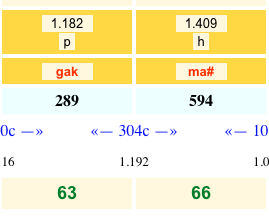
This amounts to say­ing that scale “todi2″ con­tains no map­ping of key #64 to “ga” — nor key # 65 to “ma”, see figure.

To solve this prob­lem we can recall that the scale “todi2″ was extract­ed from “Re1_murcchana”. The lat­ter con­tains all the notes of a chro­mat­ic scale in addi­tion to those extract­ed. Therefore it is suf­fi­cient to replace “_scale(todi_aak_2,0)” with “_scale(Re1_murcchana,0)” in this section:

_scale(Re1_murcchana,0) {38/10, pa2 ga2 pa2 dhak2 _ pa2 _} _scale(todi_aak_2,0) etc.

The scale edi­tor takes care of assign­ing a key num­ber to each note based on the chro­mat­ic scale if a stan­dard English, Italian/French or Indian note con­ven­tion is used. In oth­er cas­es this map­ping should be done by hand. Designers of micro­ton­al scales should be aware of key map­pings when using cus­tom names for “notes”.

Another prob­lem is that in “todi_aak_2″ note “dhak” has been raised from 792 to 810 cents, which is not its val­ue in “Re1_murcchana”. This can be fixed by cre­at­ing anoth­er vari­ant of the scale with this cor­rec­tion, or sim­ply using the pitch­bend to mod­i­fy “dhak2” — in which case the same pitch­bend could have been used to raise “gak2” in the first place.

Finally, the best way to avoid this prob­lem would be to use the source chro­mat­ic scale “Re1_murcchana”, a mur­ccha­na of Ma-grama, to con­struct raga scales even though some notes will nev­er be used.

To conclude…

This whole dis­cus­sion has been tech­ni­cal. There is no musi­cal rel­e­vance in try­ing to asso­ciate plucked notes with very sub­tly orna­ment­ed melod­ic move­ments. The last excerpt (2 rep­e­ti­tions) will prove — if it is need­ed at all — that the into­na­tion of Indian ragas is much more than a sequence of notes in a scale, what­ev­er its accuracy:

S --> AsadAliKhan3
AsadAliKhan3 --> scale(todi_aak_3,0) 94/100 {26/10,sa3}{23/10,sa3 rek3 gak3}{195/100,ma#3}{111/100,rek3}{24/10,rek3 sa3}{33/10,sa3 sa3}{71/100,rek3}{76/100,gak3}{71/100,dhak3 ma#3}{176/100,dhak3}{75/100,sa4}{27/10,dhak3__ sa4}{620/100,sa4 dhak3 ma#3 dhak3 ma#3 gak3 _ ma#3 dhak3 dhak3&}{266/100,&dhak3}{672/100,pa3____ pa3_ pa3 pa3 pa3__}{210/100,pa3 ma#3 pa3 dhak3}{222/100,dhak3}{163/100,gak3 ma#3}{426/100,gak3_ rek3____}{346/100,sa3}

Listen to Asad Ali Khan’s actu­al per­for­mance of raga Todi to appre­ci­ate its expres­sive power!

Attempting to fol­low the intri­ca­cies of alankara (note treat­ment) with a sim­plis­tic nota­tion of melod­ic phras­es demon­strates the dis­con­nec­tion between ‘model-based’ exper­i­men­tal musi­col­o­gy and the real­i­ty of musi­cal prac­tice. This explains why we have relied on descrip­tive mod­els (e.g. auto­mat­ic nota­tion) cap­tured by the Melodic Movement Analyser or com­put­er tools such as Praat, rather than attempt­ing to recon­struct melod­ic phras­es from the­o­ret­i­cal mod­els. Experiments with scales deal with the “skele­tal” nature of into­na­tion, which is a nec­es­sary but not suf­fi­cient para­me­ter for describ­ing melod­ic types.

All exam­ples shown on this page are avail­able in the bp3-ctests-main.zip sam­ple set shared on GitHub. Follow the instruc­tions on Bol Processor ‘BP3’ and its PHP inter­face to install BP3 and learn its basic oper­a­tion. Download and install Csound from its dis­tri­b­u­tion page.

Bernard Bel — Dec. 2020

---

References

Arnold, E.J.; Bel, B. L’intonation juste dans la théorie anci­enne de l’Inde : ses appli­ca­tions aux musiques modale et har­monique. Revue de musi­colo­gie, JSTOR, 1985, 71^e (1-2), p.11-38.

Arnold, E.J. A Mathematical mod­el of the Shruti-Swara-Grama-Murcchana-Jati System. Journal of the Sangit Natak Akademi, New Delhi 1982.

Arnold, E.J.; Bel, B. A Scientific Study of North Indian Music. NCPA Quarterly Journal, vol. XII Nos. 2 & 3, Bombay 1983.

Arnold, W.J. Playing with Intonation. ISTAR Newsletter Nr. 3-4, June 1985 p. 60-62.

Bel, B. Musical Acoustics: Beyond Levy’s “Intonation of Indian Music”. ISTAR Newsletter Nr 2, April 1984.

Bel, B. A Mathematical Discussion of the Ancient Theory of Scales accord­ing to Natyashastra. Note interne, Groupe Représentation et Traitement des Connaissances (CNRS), March 1988a.

Bel, B. Raga : approches con­ceptuelles et expéri­men­tales. Actes du col­loque “Structures Musicales et Assistance Informatique”, Marseille 1988b.

Bel, B.; Bor, J. Intonation of North Indian Classical Music: work­ing with the MMA. National Center for the Performing Arts. Video on Dailymotion, Mumbai 1984.

Bharata. Natya Shastra. There is no cur­rent­ly avail­able English trans­la­tion of the first six chap­ters of Bharata’s Natya Shastra. However, most of the infor­ma­tion required for this inter­pre­ta­tion has been repro­duced and com­ment­ed by Śārṅgadeva in his Sangita Ratnakara (13^th cen­tu­ry AD).

Bor, J.; Rao, S.; van der Meer, W.; Harvey, J. The Raga Guide. Nimbus Records & Rotterdam Conservatory of Music, 1999. (Book and CDs)

Bose, N.D. Melodic Types of Hindustan. Bombay, 1960: Jaico.

Hirst, D. Speech Prosody - Chapter 8. Modelling Speech Melody. Preprint, 2022.

Rao, S.; Van der Meer, W. The Construction, Reconstruction, and Deconstruction of Shruti. Hindustani music: thir­teenth to twen­ti­eth cen­turies (J. Bor). New Delhi, 2010: Manohar.

Shringy, R.K.; Sharma, P.L. Sangita Ratnakara of Sarngadeva: text and trans­la­tion, vol. 1, 5: 7-9. Banaras, 1978: Motilal Banarsidass. Source in the Web Archive.

Van der Meer, W.; Rao, S. Microtonality in Indian Music: Myth or Reality. Gwalior, 2009: FRSM.

Van der Meer, W. Gandhara in Darbari Kanada, The Mother of All Shrutis. Pre-print, 2019.

Van der Meer, W.; Rao, S. MUSIC IN MOTION. The Automated Transcription for Indian Music (AUTRIM) Project by NCPA and UvA, 2010.

Van der Meer, W. The AUTRIM Project, Music in Motion, 2020.

Initial feedback

This project began in 1980 with the found­ing of the International Society for Traditional Arts Research (ISTAR) in New Delhi, India. We had pro­duced joint arti­cles and pro­pos­als which enabled us (Arnold and Bel) to receive a grant from the International Fund for the Promotion of Culture (UNESCO). A book­let of ISTAR projects was then print­ed in Delhi, and a larg­er team received sup­port from the Sangeet Research Academy (SRA, Calcutta/Kolkata), the Ford Foundation (USA) and the National Centre for the Performing Arts (NCPA, Bombay/Mumbai).

The fol­low­ing are extracts from let­ters of sup­port received dur­ing this ini­tial peri­od — after the con­struc­tion of the Shruti Harmonium and dur­ing the design of the Melodic Movement Analyser. (ISTAR book­let, 1981 pages 20-22)

In fact, the full poten­tial of this approach can only be realised now, tak­ing advan­tage of the (vir­tu­al­ly unlim­it­ed) dig­i­tal devices that are replac­ing the hard­ware we cre­at­ed for this pur­pose 40 years ago!

---

The work of Mr. Arnold and Mr. Bel, as much from the the­o­ret­i­cal point of view as from the point of view of the prac­ti­cal real­iza­tion, appears to be one of the best of these last years, as con­cerns the musi­cal analy­sis of the clas­si­cal music of India…
— Igor REZNIKOFF, Director, UER of Philosophy, History of Art and Archeology, Mathematics, University of Paris X - Nanterre.

I con­sid­er that this work presents the great­est inter­est and is capa­ble of con­sid­er­ably advanc­ing the under­stand­ing of the prob­lem of the use of micro-intervals in the music of India, and more gen­er­al­ly, that of the inter­vals found in dif­fer­ent modal musics.
— Gilbert ROUGET, Director of Research at CNRS, in charge of the Department of Ethnomusicology at the Musée de l’Homme, Paris.

The ideas and con­cep­tions of Mr. Arnold and Mr. Bel seem tome to have the utmost inter­est musi­cal­ly because they rest not just on pure the­o­ries; but on a pro­found under­stand­ing of melod­ic and modal music, etc. The project which Mr. Bel pre­sent­ed to me could bring about a real­iza­tion much more inter­est­ing and effec­tive than that of the var­i­ous “mel­o­graphs” which have been pro­posed…
— Émile LEIPP, Director of Research at the CNRS, Director of Laboratoire d’Acoustique, University of Paris VI.

The project enti­tled “A Scientific study of the modal music of North India” under­tak­en by E. James Arnold and Bernard Bel is very inter­est­ing and full of rich poten­tials. This col­lab­o­ra­tion of math­e­mat­ics and phys­i­cal sci­ences as well as engi­neer­ing sci­ences on the one hand, and Indology and Indian lan­guages, musi­col­o­gy, as well as applied music on the oth­er hand can be rea­son­ably expect­ed to yield fas­ci­nat­ing results.
— Dr. Prem Lata SHARMA, Head of the Department of Musicology and Dean of the Faculty of Performing Arts, Banaras Hindu University.

Mr. Arnold’s work on the log­ic of the grama-murcchana sys­tem and its ‘appli­ca­tions’ to cur­rent Indian music is a most stim­u­lat­ing and orig­i­nal piece of inves­ti­ga­tion. Mr. Arnold’s research and he and his part­ner (Mr. Bel)‘s work have immense impli­ca­tions for music the­o­ry and great val­ue for the­o­ret­i­cal study of Indian music.
— Bonnie C. WADE, Associate Professor of Music, University of California

Looking for­ward into the future, it (the Shruti har­mo­ni­um) opens up a new field to com­posers who wish to escape from the tra­di­tion­al frame­work in which they are trapped, by virtue of the mul­ti­plic­i­ty of its pos­si­bil­i­ties for var­i­ous scales, giv­ing hence a new mate­r­i­al.
— Ginette KELLER, Grand Prize of Rome, Professor of Musical Analysis and Musical Aesthetics, ENMP and CNSM, Paris.

I was aston­ished to lis­ten to the “shrutis” (micro­tones) pro­duced by this har­mo­ni­um which they played accord­ing to my sug­ges­tion, and I found the ‘gand­hars’, ‘dhai­vats’, ‘rikhabs’ and ‘nikhads’ (3rds, 6ths, 2nds and 7ths) of ragas Darbari Kanada, Todi, Ramkali and Shankara to be very cor­rect­ly pro­duced exact­ly as they could be pro­duced on my vio­lin.
— Prof. V.G. JOG, Violinist, recip­i­ent of the Sangeet Natak Akademi Award.

Once again, bra­vo for your work. When you have a pre­cise idea about the cost of your ana­lyz­er, please let me know. I shall be able to pro­pose it to research insti­tu­tions in Asian coun­tries, and our own research insti­tu­tion, pro­vid­ed that it can afford it, might also acquire such an ana­lyz­er for our own work.
— Tran Van KHE, Director of Research, CNRS, Paris.

The equip­ment which Mr. E.J. Arnold and B. Bel pro­pose to con­struct in the sec­ond stage of the research which they have explained to me seems to be of very great inter­est for the elu­ci­da­tion of the prob­lems con­cern­ing scales, and into­na­tion, as much from the point of view of their artis­tic and musi­co­log­i­cal use, as from the the­o­ry of acoustics.
— Iannis XENAKIS, Composer, Paris.