Musical works encoded in the Bol Processor (using “simple notes” according to English, Italian/Spanish/French and Indian conventions) can be analysed in terms of harmonic or melodic intervals.
The musical aspects are discussed after a description of the process.
In the final section, we present a one-click method for evaluating the suitability of all documented tuning systems for a given piece of music. A demo of this analysis can be found on the Bach well-tempered tonal analysis.
Basic process
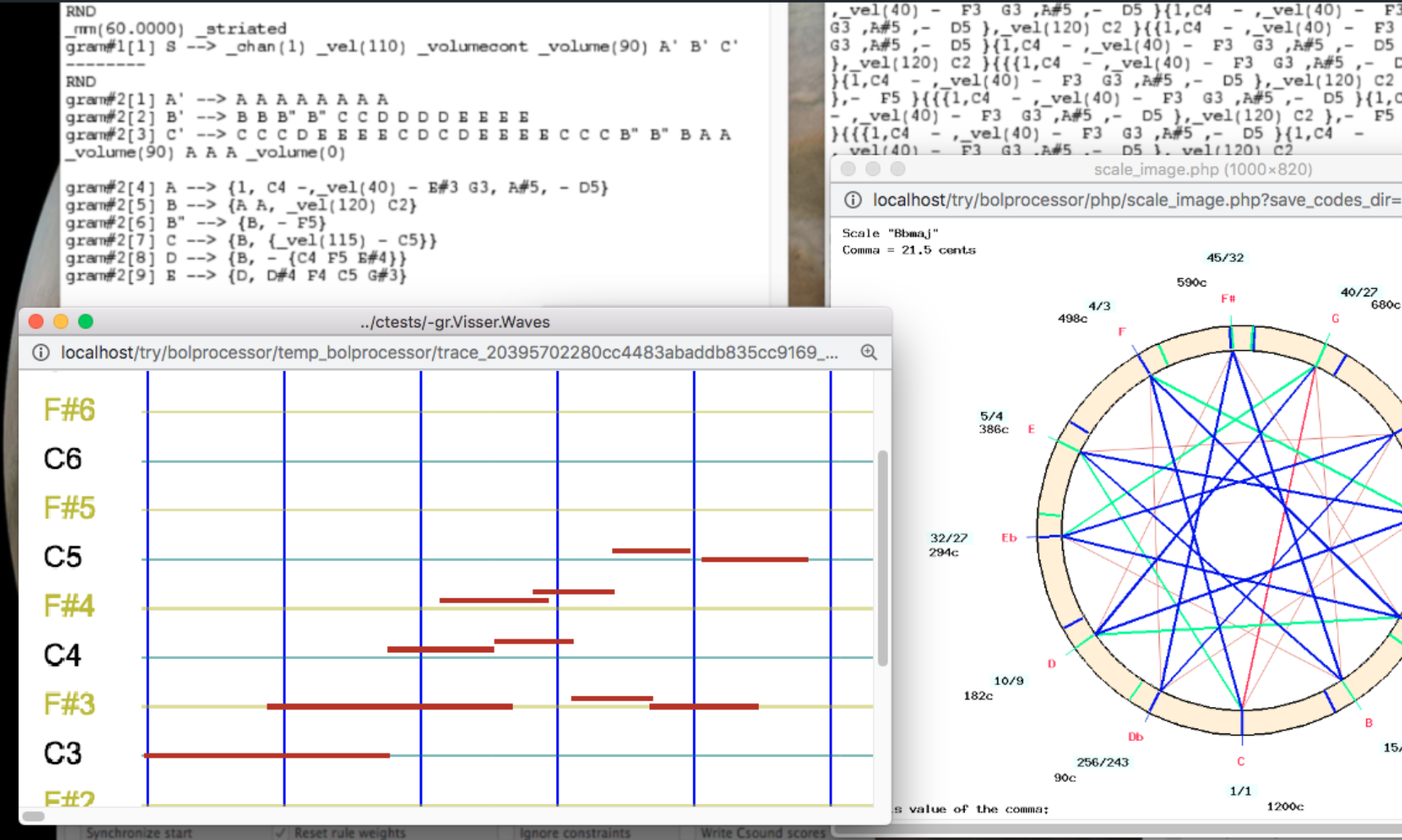
This calculation is started by pressing the ANALYZE INTERVALS button at the bottom of the ‘Data’ window:

The machine found a ‘-cs.tryTunigs’ declaration at the top of the data content, indicating that it should pick up the tonal scale definitions contained in this Csound resource. These definitions are only accessible if ‘-cs.tryTunigs’ was opened less than 24 hours ago: these files are stored in the ‘temp_bolprocessor’ folder which is automatically cleaned up of old storage. Click on the ‘open’ link if necessary.
The analytical process is demonstrated using a single phrase of François Couperin’s Les Ombres Errantes imported from a MusicXML score — see the Importing MusicXML scores page. This example is small enough to allow a visual check of the technical process, but too short to allow a meaningful musical interpretation of the result.
In Bol Processor notation (English convention), the musical item reads as follows — read the Polymetric structures page:
-cs.tryTunings_scale(rameau_en_sib,0) _rndtime(20) {_tempo(13/15) _vel(64){3, _legato(20) C5 _legato(0) {1/4,C5 B4 C5}{3/4,B4} _legato(20) Eb5,{1/2,Eb4}{5/2,G4 D4 F4 C4 Eb4},Eb4 D4 C4}} {_tempo(13/15) _vel(64){4, _legato(0) {1/4,Eb5 D5 Eb5}{3/4,D5} _legato(20) C5 _legato(0) {1/4,C5 B4 C5}{3/4,B4}{1/8,C5 B4}{7/8,C5},{4,B3 F4 Eb4 G4 D4 F4 C4 Eb4},B3 Eb4 D4 C4}}
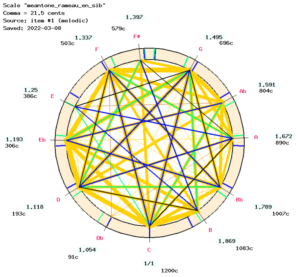
The sound production used the Csound resource file ‘-cs.tryTunings’ which contains the tonal scale ‘rameau_en_sib’ — see the page Comparing temperaments. This scale probably provides the best tuning for this piece when played on a “harpsichord-like” Csound instrument.
The machine has picked up a definition of the tonal scale in a temporary copy of ‘-cs.tryTunings’. The essential content of this definition is the set of tonal positions in the scale shown in the image — see the Microtonality page.
Click on the ANALYZE INTERVALS button and the following screen appears:

The table above gives a summary of matching intervals: pairs of notes played one after the other (melodic) or one above the other (harmonic), distinguishing between ascending and descending melodic intervals. These matches can be checked in the graphical representation of this item:
Intervals are listed in descending order of importance. For example, the melodic interval ‘C’ to ‘B’ occurs in 20.3 beats, the highest number. Ascending melodic intervals ‘B’ to ‘F’ and ‘D’ to ‘B’ are the least frequent. Values less than 5% of the maximum in the column are ignored in the graphical display.
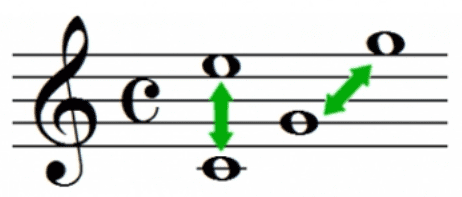
Interestingly, the highest scores of harmonic intervals in this musical phrase are minor thirds such as ‘D’/‘B’ and ‘C’/‘Eb’. The fifth ‘C’/‘G’ is scored only 1.6 beats, which is 18% of the highest score.
The detection of a “harmonic interval” is based on the comparison of its start and end dates with options that can be modified. Let $start1, $end1, $start2 and $end2 be the timings of two notes. We assume $start2 >= $start1 due to a preliminary chronological sorting of the list of notes. The matching_intervals() function does the following to evaluate harmonic intervals:
$duration1 = $end1 - $start1;
$duration2 = $end2 - $start2;
$overlap = $end1 - $start2;
$smallest_duration = $duration1;
if($duration2 < $duration1) $smallest_duration = $duration2;
if($smallest_duration < $min_dur) return FALSE;
if($start1 + ($duration1 / 2.) < $start2) return FALSE;
if($overlap < ((1 - $ratio) * $smallest_duration)) return FALSE;
return TRUE;
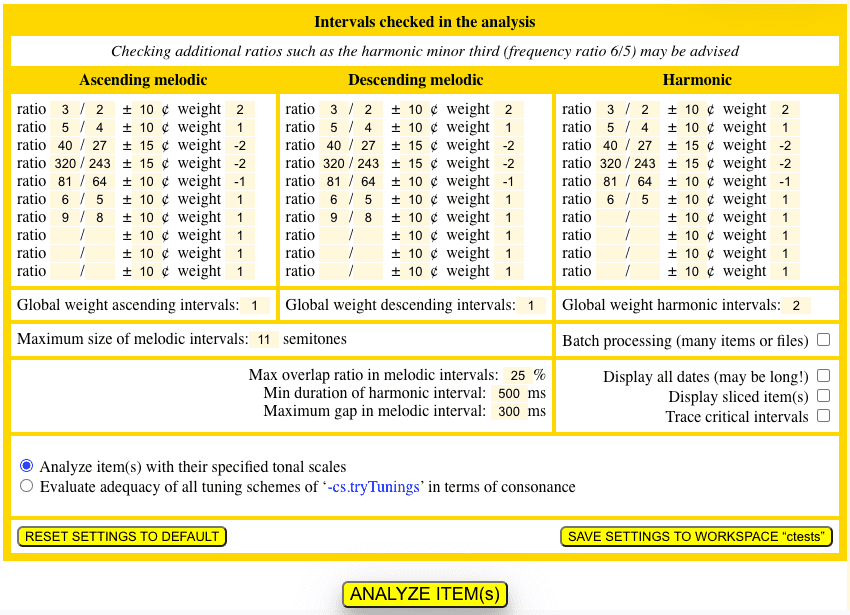
This function eliminates brief overlaps of time intervals, such as those created by slurs interpreted as _legato() performance controls when importing MusicXML scores — see details. It also eliminates notes with durations less than $min_dur, optionally set to 500 milliseconds. For example, short notes such as ‘C5’, ‘B4’, ‘Eb5’, etc., are discarded. Finally, it checks that $overlap is greater than a fraction of the smallest duration, with $ratio set to 0.25 by default. Another option, not shown here, is the maximum tonal distance between two notes, which is set to 11 semitones by default.
The conditions for matching melodic intervals are similar:
if($start2 > ($end1 + $max_gap)) return FALSE;
if($start1 + ($duration1 / 2.) >= $start2) return FALSE;
if($overlap >= ($ratio * $smallest_duration)) return FALSE;
return TRUE;
The $max_gap parameter (typically 300 milliseconds) is the maximum delay between the end of the first note and the beginning of the next one.
All parameters can be changed before the process is restarted. These settings are discussed later:
Calculations

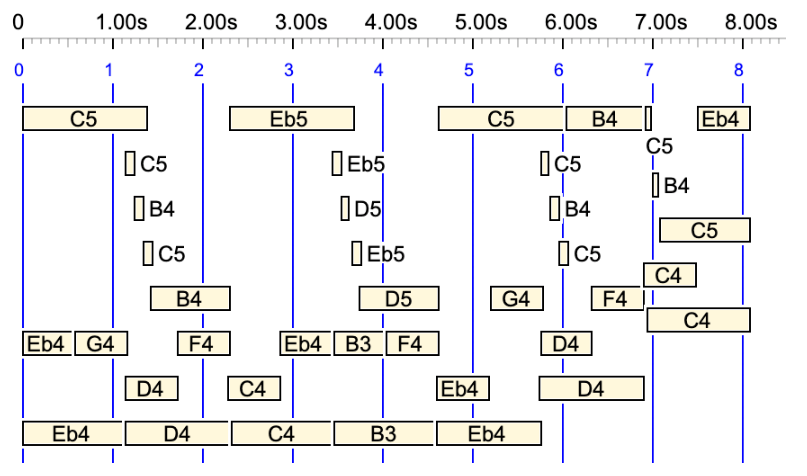
To check the sequence of time intervals in great detail it is possible to activate the “Display all dates” option yielding a detailed analysis.
All matching intervals will be listed. It is not practical to use this option on large pieces of music…
Dates are in seconds, rounded to 0.1s, although more accurate values are used. In fact, all time calculations are based on whole numbers, as in the Bol Processor console.
The result is always debatable. For example, some melodic or harmonic intervals may appear “accidental” rather than significant.
For this and other reasons, it may be necessary to explore other options related to musical and performance styles.
Graphic display
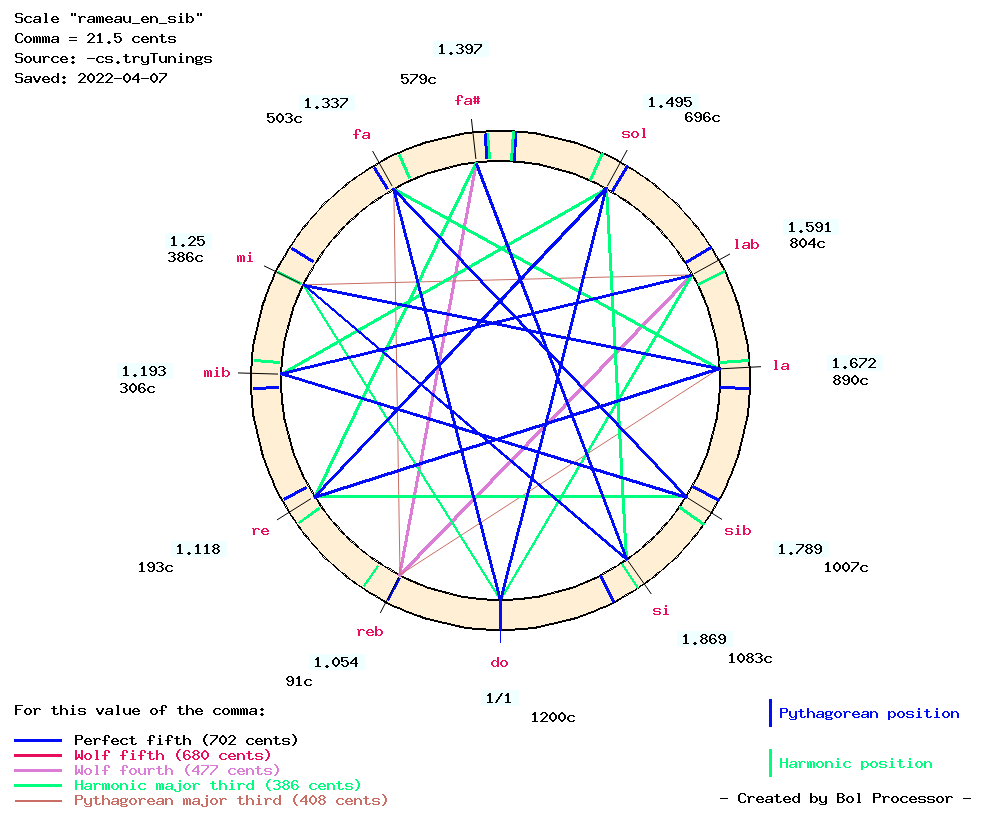
Melodic and harmonic tonal intervals are displayed against the background of the tonal scale used for the performance. Here it would be ‘rameau_en_sib’, although by default an equal-tempered scale is used.
Clicking on the links to the harmonic interval pictures (see image above) will bring up the following three graphs — in separate and resizable windows:
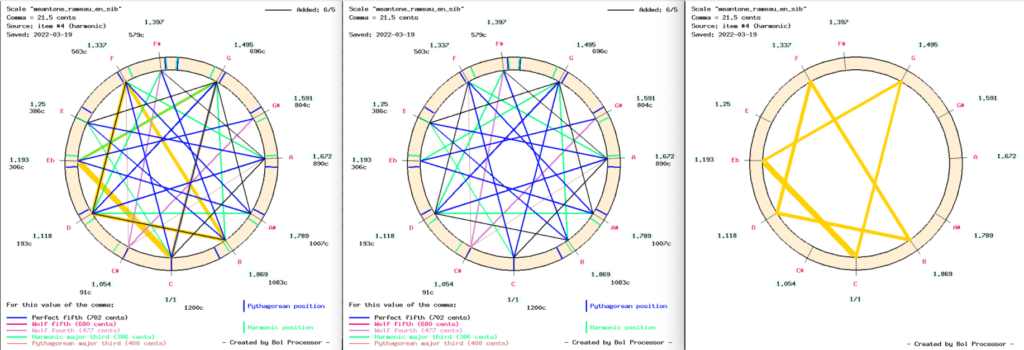
Intervals are shown as gold highlights with widths proportional to their relative values. In the left-hand image, these golden segments are drawn behind the fifths, major and minor thirds marked on the scale. For this reason, the yellow highlighting of the link between Eb and G, behind the green link of a harmonic major third, is less visible in the full image.
Minor thirds (ratio 6/5) have been added to the settings. For this reason, those available in this scale are shown as black segments. These additional ratios are listed at the top right of each image.
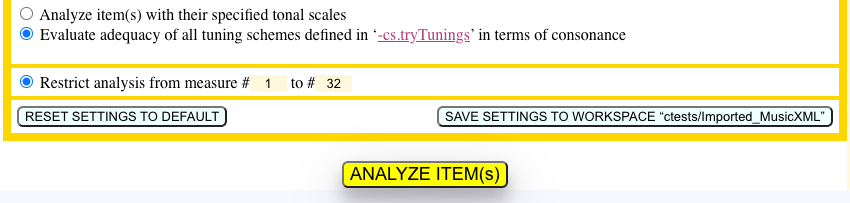
Restricted analysis
If a MusicXML file has been imported along with bar numbers (notated [—1—], [—2—] etc.), these can be used to restrict the analysis to a subset of the score.
Below is the setting of bars #1 to #32 (the Aria) in J.S. Bach’s Goldberg Variations:
Restricting the tonal analysis to the Aria in the Goldberg Variations makes sense because other variations, due to their high speed, do not show harmonic intervals longer than the minimum duration fixed in the settings (500 ms).
Musical discussion
Tonal analysis with the Bol Processor aims to help choose the most appropriate tuning system for a piece of music — a temperament as defined by Baroque musicians. This topic is covered on the page Comparing temperaments.
We first describe a visual method for estimating (rather than measuring) the adequacy of a tuning system for the performance of musical works imported from MusicXML scores — read the page on this topic. In the next section, we will show how to automatically compare all candidate scales, taking into account the relevant parameters revealed in this section.
Take, for example, J.S. Bach’s Prelude 1 in C major for which some historical information (reported by Asselin, 2000 p. 142) suggests the choice of a Kirnberger temperament. Which one?
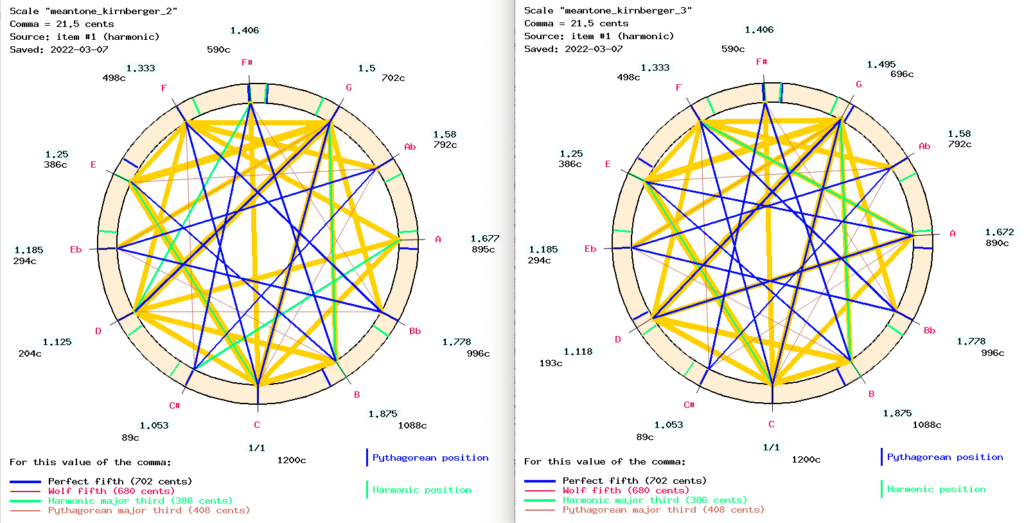
The full representation of the harmonic intervals is shown above and compared with two different scales described by Kirnberger (Asselin, 2000 p. 90, 93). The match looks better on the right (Kirnberger III). For example, the interval ‘D’ - ‘A’ is closer to a “pure” fifth (702 cents) on Kirnberger III (697) than on Kirnberger II (691). Another significant match is the harmonic major third ‘F’ - ‘A’. Other intervals are similar in terms of these scales.
A careful listening to both versions might confirm this mechanical analysis:
For François Couperin’s Les Ombres Errantes, the same crude analysis yields no significant result. Harmonic interval analysis may be less relevant because this piece is more generally perceived as a sequence of melodic intervals, including minor thirds and major seconds. This can be seen in the graph of melodic intervals:
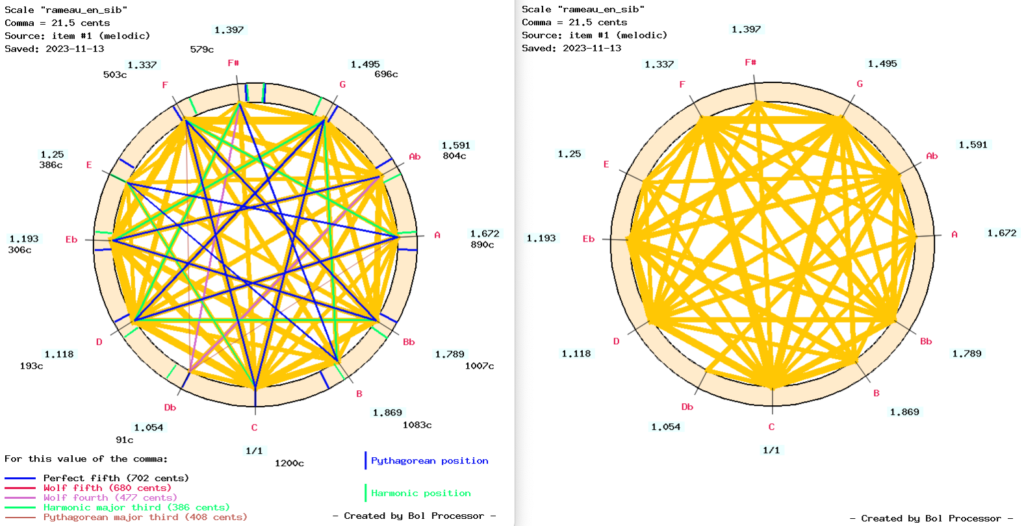
Comparing this graph with the ‘rameau_en_sib’ scale does not reveal any interesting patterns, for the simple reason that neither minor thirds nor major seconds have been taken into account in this scale in terms of “just intonation” — see page Just intonation: a general framework. Although we can assume that a Pythagorean major second (ratio 9/8) sounds more “consonant” than a harmonic one (ratio 10/9), there is no reason to systematically claim that the harmonic minor third (ratio 6/5) is “better” than the Pythagorean one (ratio 32/27).
The picture on the left shows that the frequent melodic intervals of major thirds emphasise the harmonic major thirds (ratio 5/4) of this scale.
We need to check intervals smaller than the major third in the tonal scales. If we tell the machine to check intervals close (within ± 10 cents) to the harmonic minor third (ratio 6/5), the above graphs will look like this:
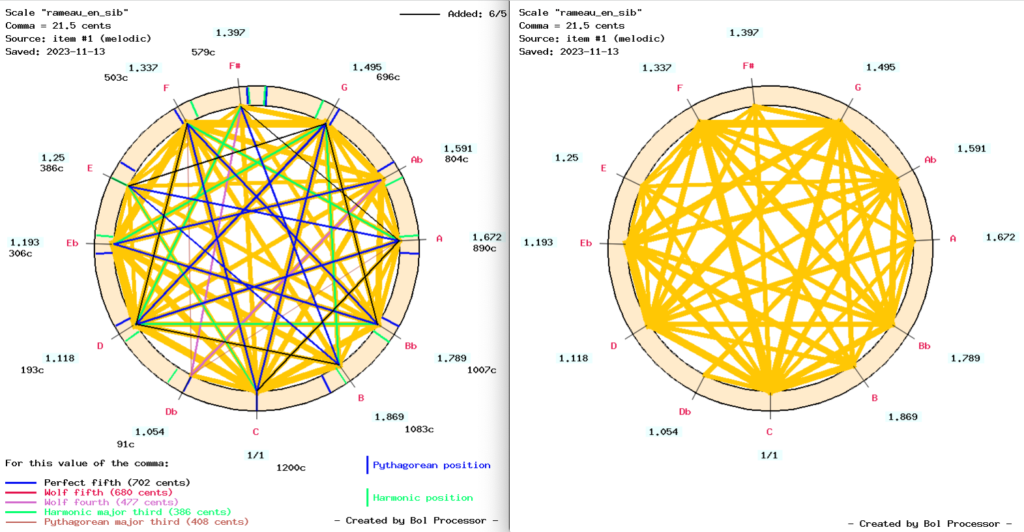
The picture on the left side shows that all the minor thirds used in this performance coincide within ± 10 cents with the harmonic minor thirds (ratio 6/5) of the scale, which is an incentive to admit that the ‘rameau_en_sib’ scale would be a fair (perhaps the best) tuning option for Les Ombres Errantes.
A counter-example is the matching of Les Ombres Errantes with a pure-minor-thirds temperament designed during in 16th century (Asselin 2000 p. 82, see figure). Below are the graphs of the matching melodic (left) and harmonic (right) intervals, with black lines marking the harmonic minor thirds (ratio 6/5):
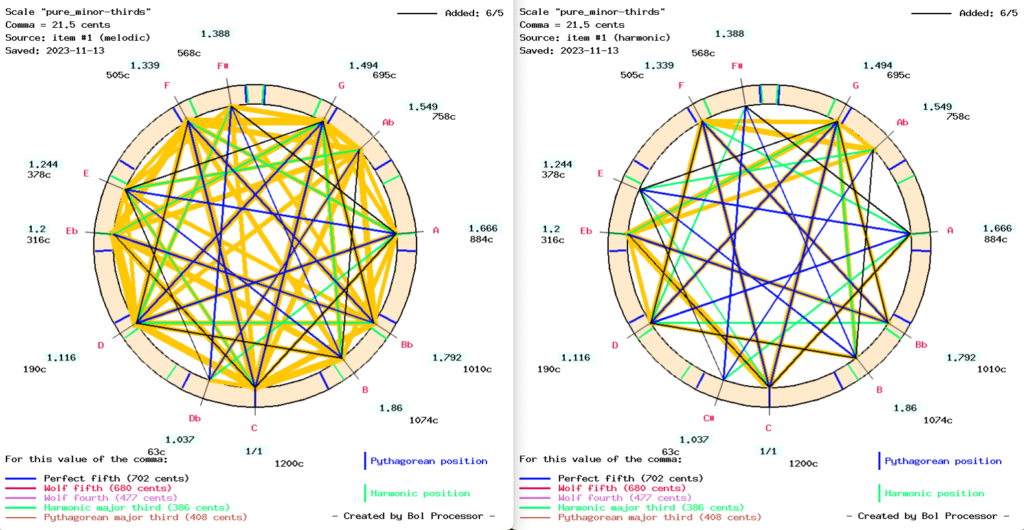
The main drawback of this ‘pure_minor_thirds’ temperament is the very low position of ‘Ab’ which is supposed to produce a consonant sequence of minor thirds: ‘Ab’ - ‘B’ - ‘D’ - ‘F’. However, ‘Ab’ - ‘B’ is not a melodic interval found in this piece, nor are ‘Db’ - ‘E’ and ‘E’ - ‘G’, which are well represented by the ‘pure_minor_thirds’ temperament. There are also discrepancies in the harmonic intervals, which are easy to hear. We can conclude that the pure minor thirds temperament is neither the best nor the worst tuning system for this musical work, although the comparison of sound productions suggests that it is significantly less good than the ‘rameau_en_sib’ scale.
➡ Comparing graphs is easy with the detached resizable pictures produced by the Bol Processor.
A “deaf musicologist’s” approach
The analysis shown so far has replaced a comparison of sound rendering — see the page Comparing temperaments — with a visual problem of pattern-matching. We have shown that Baroque musicians and tuners sought to achieve consonance in terms of simple frequency ratios for fifths (close to 3/2) and harmonic major thirds (close to 5/4). This approach and its underlying assumptions are discussed on the page Just intonation: a general framework.
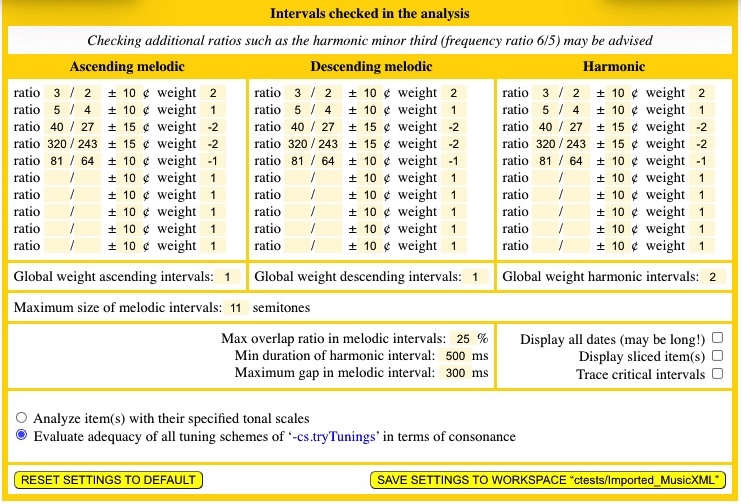
Furthermore, one might be tempted to claim that a “just intonation” minor third should be harmonic (ratio close to 6/5), but the decision should remain open. To this end, it is possible to enter an additional set of melodic and harmonic intervals that the analyst considers significant for the evaluation of tonal scales. Each interval is defined by an integer ratio — which can be as complex as necessary.
Comparative pattern matching assigns a numerical score to each scale that has been evaluated for its fit with the musical work. This allows the candidate scales to be sorted. However, two separate scores are required, one for melodic intervals and one for harmonic intervals. A weighted sum of scores is therefore used to sort the list of scales.
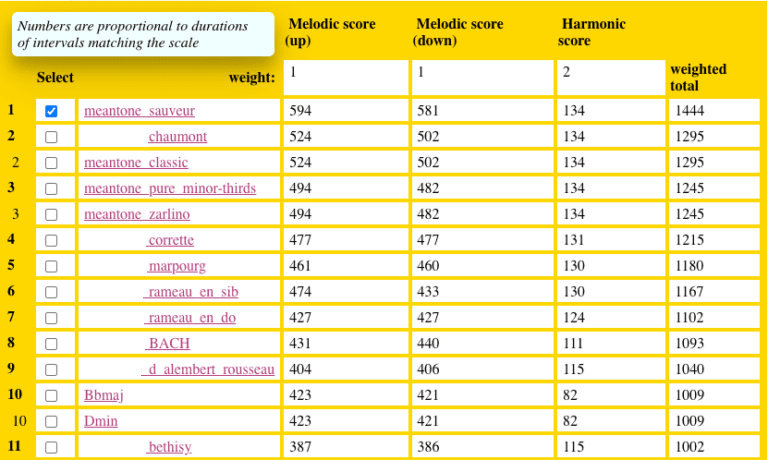
This method has been implemented in the Tonal analysis process. We have compared all the scales defined in ‘-cs.tryTunings’ — including in particular all the temperaments documented by Pierre-Yves Asselin — in terms of their suitability for the rendering of melodic and tonal intervals in François Couperin’s Les Ombres Errantes:
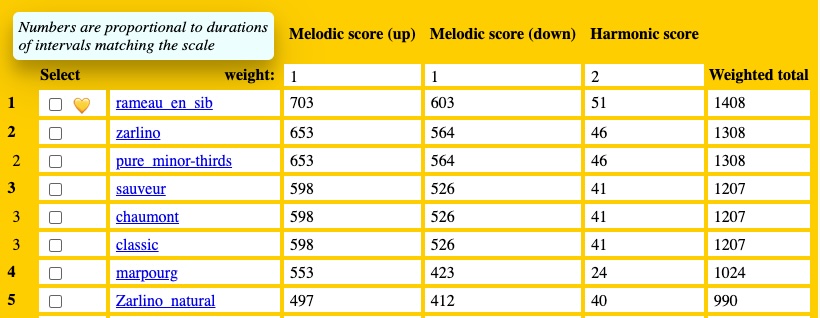
Great result! The machine confirms that the scale ‘rameau_en_sib’ is the best candidate for the interpretation of Les Ombres Errantes. Its scores are significantly better for both melodic and harmonic intervals. (A total of 45 tuning schemes were tried.)
By default, the evaluation of melodic and harmonic intervals considers only perfect fifths (3/2) and harmonic major thirds (5/4) as “good” intervals, with weights of 2 and 1 respectively, and wolf fifths (40/27), wolf fourths (320/243) and Pythagorean major thirds (81/64) as “bad” intervals, with weights of -2, -2 and -1 respectively. All these weights can be modified as shown in the image above.
We repeat the comparison with the additional option of harmonic minor thirds (6/5) as melodic intervals:
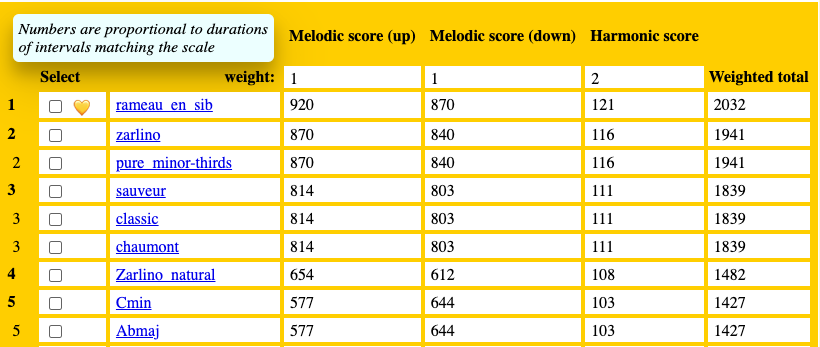
As expected, all the melodic values increased, but the winner remained. If we add the Pythagorean major second (ratio close to 9/8), we get the following:
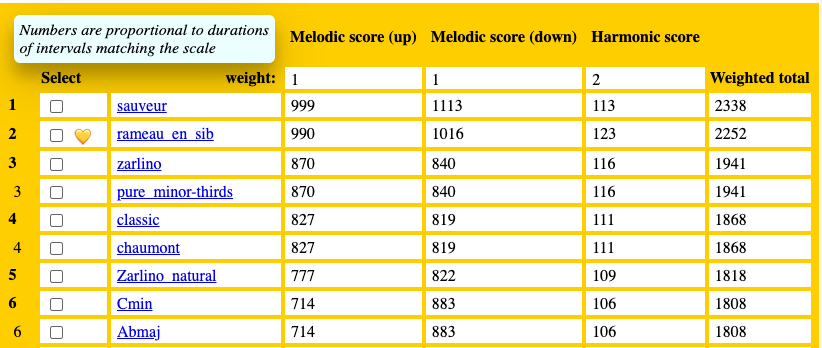
The ‘rameau_en_sib’ scale is now challenged by ‘sauveur’ for melodic intervals, but its harmonic score remains higher.
Note that scales Abmaj and Cmin are identical, which explains their equal scores.

A visual comparison of scales with melodic interval markings shows that there is little difference between these temperaments in terms of the performance of Les Ombres Errantes. Since the ‘sauveur’ temperament was designed in 1701 by the (hearing-impaired?) French mathematician Joseph Sauveur, it is not unlikely that it was used for the composition of Les Ombres Errantes in 1730.
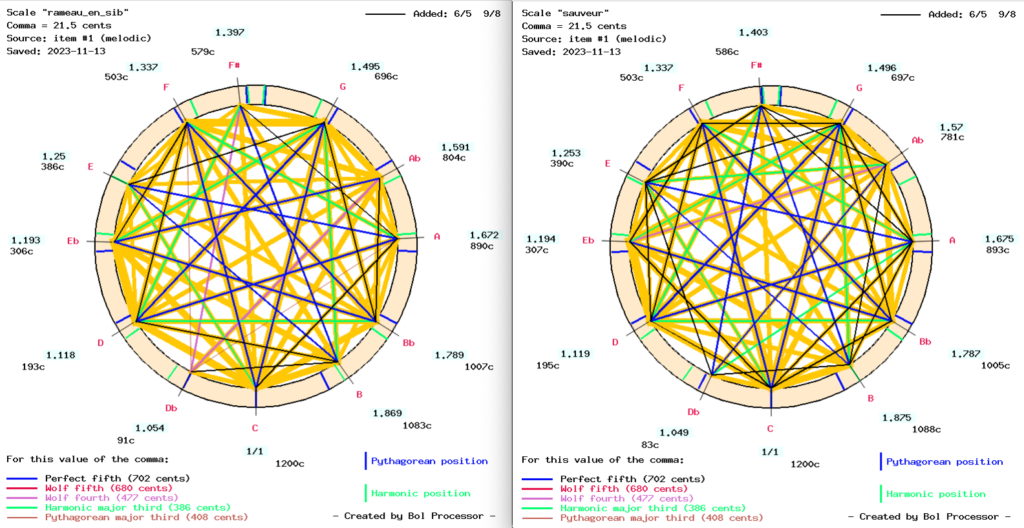
The scale ‘rameau_en_sib’ again scores as good as ‘sauveur’ when the Pythagorean minor third (ratio close to 32/27) is tried as a melodic interval (both ascending and descending) in place of the ratio 6/5… This is due to the use of ‘F’ - ‘Ab’, which is rendered as a Pythagorean minor third by ‘rameau_en_sib’, but not by ‘sauveur’.
Many more checks can be made by changing the weights assigned to the occurrences of melodic and harmonic ratios. Finding the best settings requires a thorough study of the musical score — this is where human musicologists come in!
Ears (plus expert knowledge of the score) could make the final decision:
The analytical process we are following is a kind of reverse engineering… Obviously, composers did not search for a suitable temperament after creating a musical work. It is more realistic to assume that they composed works on existing instruments, with the effect that sets of pieces produced by the same composer (using the same instrument) at a given time obeyed implicit melodic and harmonic constraints that best suited the tuning of their instrument(s).
Comparative study
Let us look again at J.S. Bach’s Prelude 1 in C major, for which Kirnberger III was chosen (visually) as a better match than Kirnberger II. Including the ratios 6/5 and 9/8 as possible melodic up/down intervals, and 6/5 as a harmonic interval, the following classification of tuning schemes emerges:
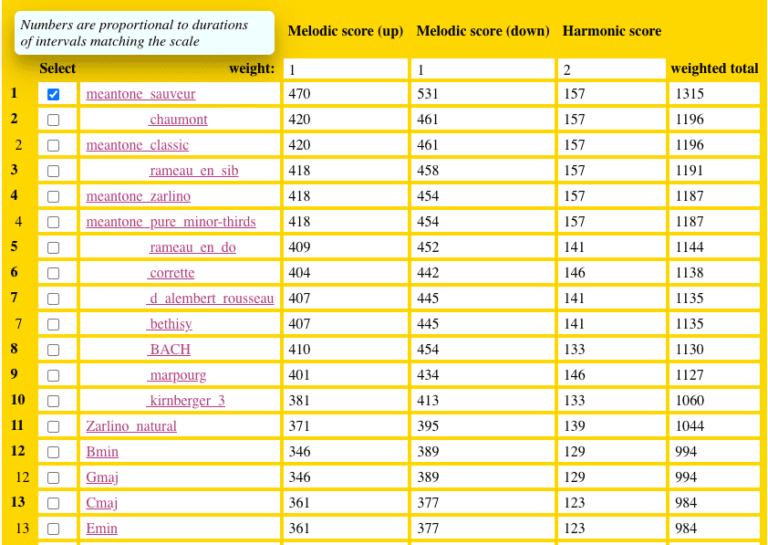
The winner is undoubtedly ‘sauveur’ although the harmonic score is identical for six temperaments, but ‘kirnberger_3′ scores much lower.
Note that this was achieved by declaring ratios close to 6/5 as possible consonant melodic and harmonic intervals. For a discussion of this hypothesis, see Bach well-tempered tonal analysis for a discussion of this hypothesis.
Sauveur’s temperament is the best suited because of its high proficiency in harmonic minor thirds (6/5) and Pythagorean major seconds (9/8). It also has a complete set of perfect fourths and fifths (3/2) except for the wolf fourth ‘D#’ - ‘G#’, which is almost 477 cents (instead of 498). Fortunately, this interval is never used in Bach’s piece:
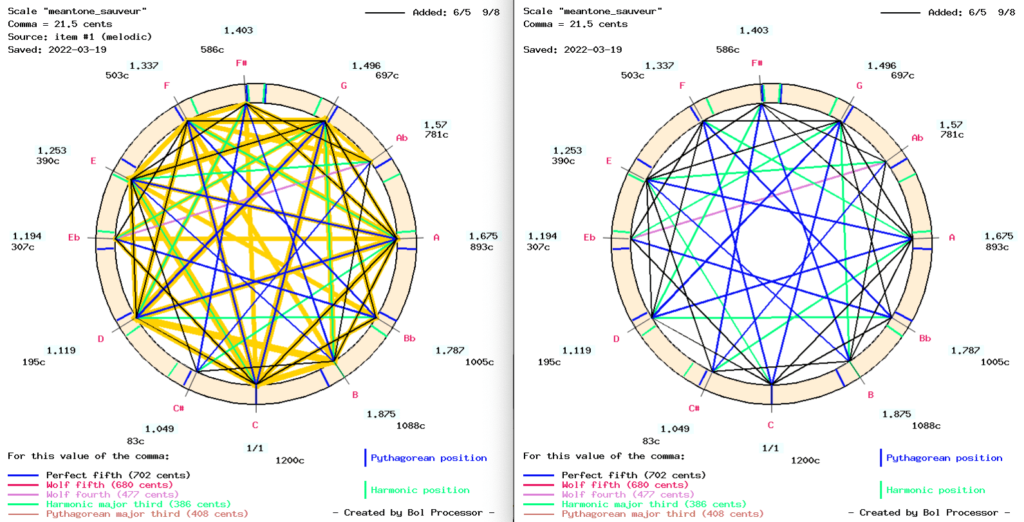
This rendering can be compared (in terms of tunefulness) with a human performance on a real harpsichord:
Unsurprisingly, J.S. Bach’s Fugue 1 in C major shares the same preference for ‘sauveur’, with other tuning schemes following in a different order. All of the fugues in this series of works (books I and II) are associated with preludes in the same key.
The tonal analysis of J.S. Bach’s Prelude 2 in C minor again selects ‘sauveur’ using the same evaluation criteria — including the ratios 6/5 (melodic and harmonic) and 9/8 (melodic up/down). The scoring is completely different, but the winner is unchanged, although it is challenged by ‘rameau_en_sib’ for its harmonic score.
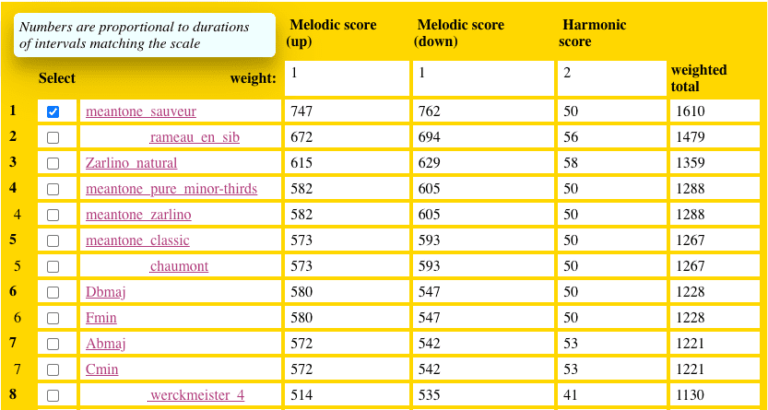
Note that the Cmin scale has a bad rate because of the melodic intervals. It beats Sauveur’s temperament in terms of harmonic intervals, but these are relatively rare in this prelude. This classification could be quite different if some ratios (such as 9/8) were ignored for the evaluation of melodic intervals. Even ratios close to Pythagorean thirds (81/64) may sound acceptable in fast melodic movements — see the page on Bach well-tempered tonal analysis.
J.S. Bach’s Fugue 2 in C minor again favours ‘sauveur’.
We get the same result with J.S. Bach’s Prelude 6 in D minor (random choice). Note the strikingly high melodic scores of ‘sauveur’:
J.S. Bach once claimed that he could play his entire repertoire on the instrument he had tuned by himself. This sounds like squaring the circle, and many hypotheses have been put forward to solve this problem for das Wohltemperierte Clavier.
These examples suggest that Sauveur’s temperament may have been Bach’s choice. Although there is little chance that the German composer (1685-1750) would have heard of the research work of the French physician (1653-1716), the systematic construction of this temperament — a single sequence of fifths diminished by 1/5 comma (see image and read Asselin, 2000 p. 80) — suggests that any composer could have worked it out independently.
To test (and challenge) this hypothesis, we have undertaken a tonal analysis of 24 preludes and fugues from books I and II of The Well-Tempered Clavier using the same settings. Read the Bach Well-tempered tonal analysis page. This large spectrum analysis requires a batch processing device, which we will now describe.
Batch processing
To analyse the tonality of a large number of musical works, we need to create a Data page containing the names of all the pages containing the Bol Processor scores of these items. For example, the page “-da.index_preludes_book_I” is as follows:
When reading this page, the Tonal analysis procedure opens each data file and picks up the Bol Processor score it contains. To facilitate this, the Batch processing option can be checked in the settings.
In the batch-processing mode, the machine will not display the full set of scales for each piece of music analysed. If the score contains a specification for a tonal scale — a _scale(some_scale, 0) instruction — the list of preferred scales will be displayed down to the specified one. If the specified scale is the first in the ranking, then the next two following scales are listed. If no scale is given, only the 10 best matching scales are listed:
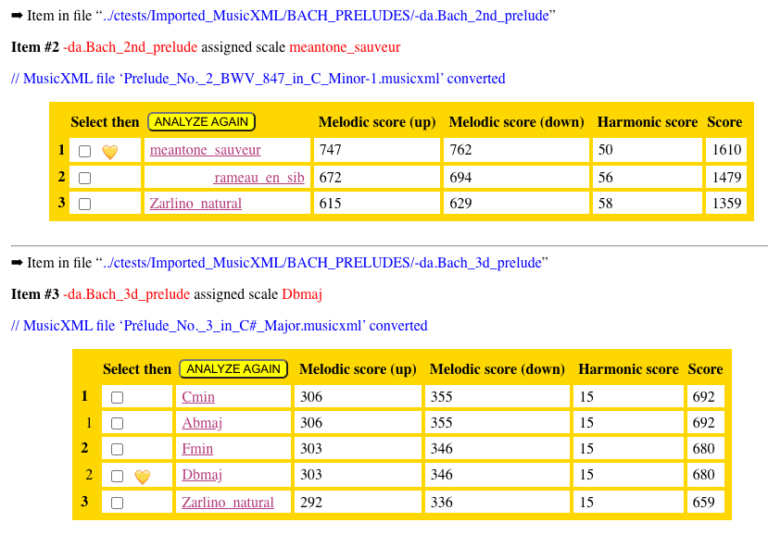
Items #2 and #3 contain the specifications of tonal scales sauveur and Dbmaj respectively.
This preference is confirmed by the analysis of item #2 but it is not the case with item #3.
At the bottom of the page, a SHOW RESULTS button displays a downloadable HTML file containing all the results:
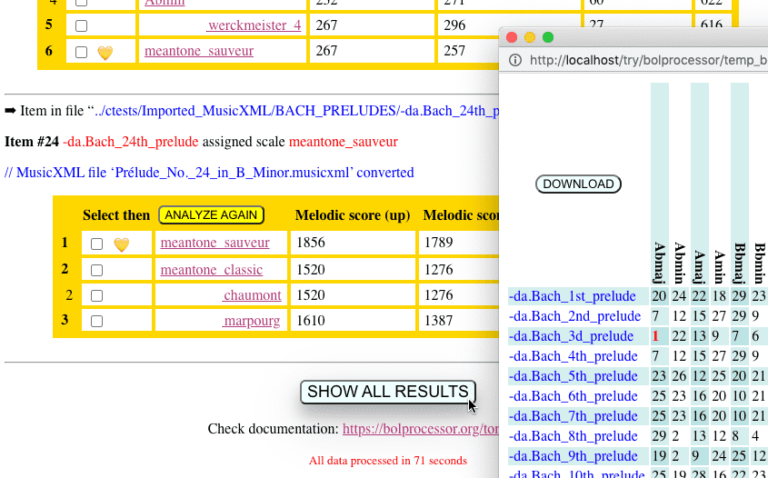
The HTML page also shows the settings for the analysis, and can be downloaded, along with a CVS file of the same figures, which is suitable for statistical graphing.
The results of the analysis of all the preludes and fugues of The Well-tempered Clavier are published and discussed on the page Bach well-tempered tonal analysis.
Does it apply to western classical music?
The analysis of tonal intervals and their correspondence to documented tuning systems (temperaments) makes sense in the context of Baroque music, assuming that composers and instrument tuners sought to achieve maximum consonance in the performance of their musical repertoire. The question remains whether it is equally reliable (and useful) for the analysis of musical works from more recent periods.
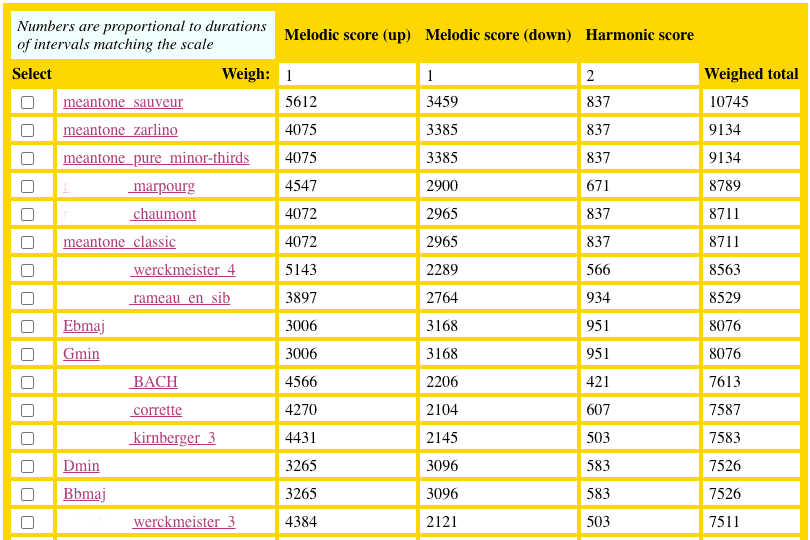
The best score — once again — is that of Sauveur’s temperament, mainly because of the ascending melodic intervals. If performers are trying to achieve ratios 9/8, 6/5, 5/4 and 3/2, then ‘sauveur’ may be the best representation of the “tuning scheme” they have in mind.
The equal temperament scale comes last, with scores of 3529, 1680 and 240 for ascending melodic, descending melodic and harmonic intervals respectively. Part of the explanation lies in the comparison of the two scales as a background to the harmonic intervals:
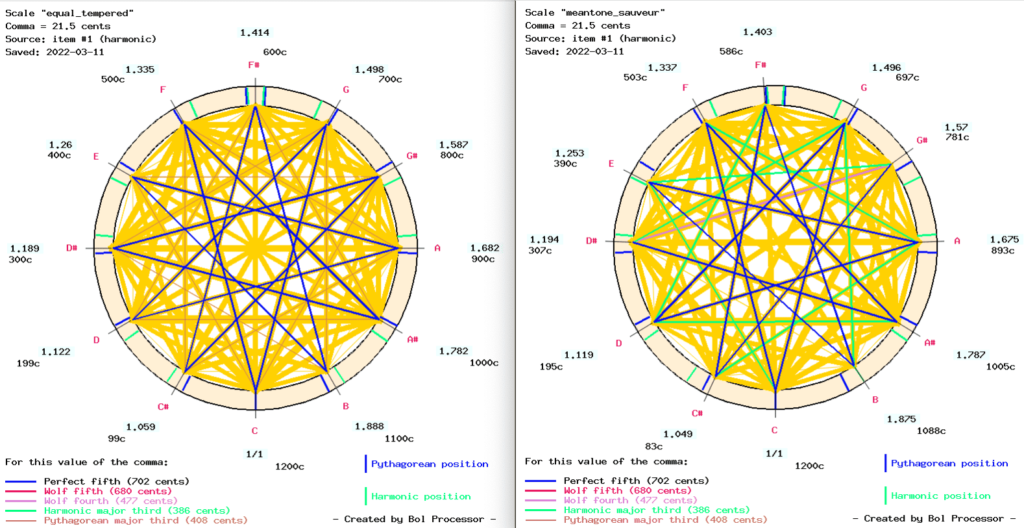
The most obvious difference is the use of almost perfect harmonic major thirds (ratio 5/4) on Sauveur’s scale (see image) instead of Pythagorean major thirds (approximately ratio 81/64) on the equal tempered scale (see image). The former have been assigned weights (+1) and the latter (-1). Yellow background lines indicate that these intervals are used quite frequently.
One drawback of Sauveur’s scale is the wolf fourth ‘D#’ - ‘G#’ (approx. 477 cents), but this interval does not occur frequently in the score.
Many other observations could be made, comparing the values of the melodic intervals, and the whole process (which took almost 8 minutes) could be started again with different settings of the weights, giving more or less importance to certain intervals. After all, we do not know whether an expert player of a string instrument would play minor thirds at intervals of 6/5, 32/27, tempered, or some other value, and even more so, whether these values depend on the harmonic/melodic context of each musical phrase.
This suggests that we shouldn’t get too excited about a (still primitive) tonal analysis tool when it comes to sophisticated tonal material…
Reference
Asselin, P.-Y. Musique et tempérament. Paris, 1985, republished in 2000: Jobert. Soon available in English.
➡ Musicians interested in continuing this research and related development can use the current version of Bol Processor BP3 to process musical works and implement further tuning procedures. Follow the instructions on the Bol Processor ‘BP3’ and its PHP interface page to install BP3 and learn its basic operation. Download and install Csound from its distribution page.