Posted on by Bernard Bel

Bach well-tempered tonal analysis

Harpsichord jacks in a com­plet­ed harp­si­chord
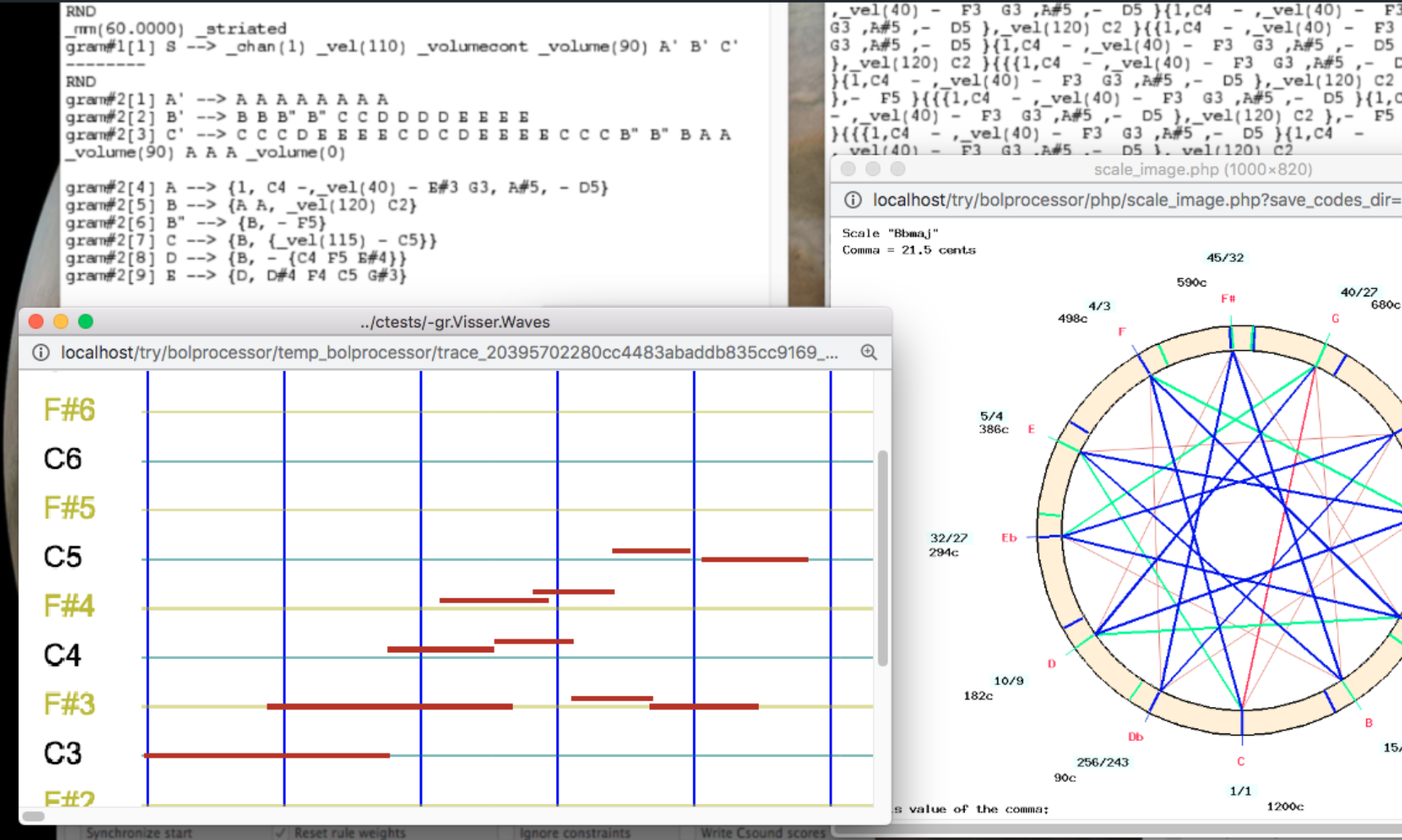
Source: Material Matters

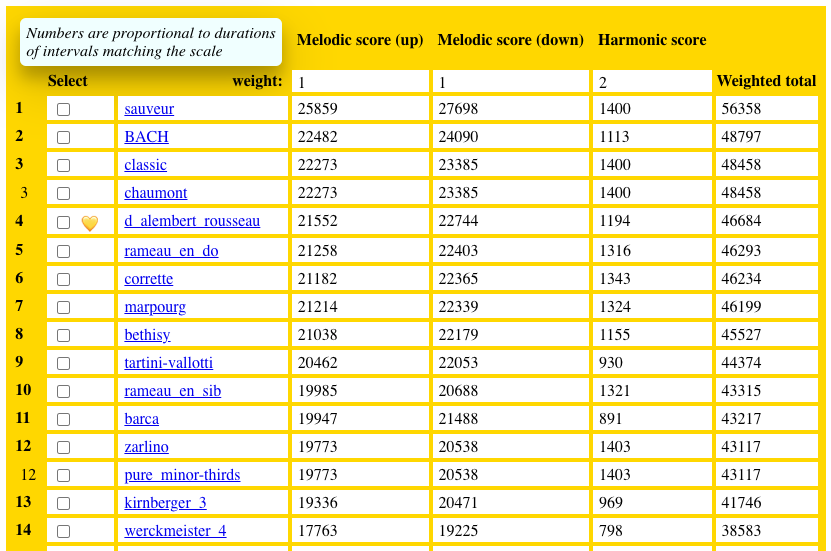
The fol­low­ing is a “com­pu­ta­tion­al” tonal analy­sis of musi­cal works by J.S. Bach known as The Well-tempered Clavier, books II and II, pub­lished cir­ca 1722 and 1742 respec­tive­ly, and Goldberg Variations (1741).

All musi­cal scores have been con­vert­ed from MusicXML to Bol Processor syn­tax — read Importing MusicXML scores. This tonal analy­sis is pro­duced by Bol Processor’s tonal batch-processing tool.

The aim of this exer­cise was to match each musi­cal work against a set of tun­ing schemes described and imple­ment­ed on the Bol Processor. These com­prise all tem­pera­ments doc­u­ment­ed by Pierre-Yves Asselin ([1985], 2000) and “nat­ur­al” scales con­struct­ed sys­tem­at­i­cal­ly — read Creation of just-intonation scales.

It was assumed that the best match for a scale points at the tun­ing scheme fit for the inter­pre­ta­tion of a musi­cal work. This assump­tion is based on the hypothe­ses that (1) musi­cians and com­posers of the Baroque peri­od aimed at achiev­ing opti­mum “con­so­nance”, and that (2) this notion implied a pref­er­ence for cer­tain inter­vals expressed as inte­ger ratios. These state­ments are dis­cussed on this page. Accurately tuned sound exam­ples are pro­posed for an audi­tive assess­ment of results.

The inter­est of this tonal analy­sis goes beyond the com­pre­hen­sion of music the­o­ry and prac­tice. Its epis­te­mo­log­i­cal dimen­sion is the trust­wor­thi­ness of math­e­mat­i­cal “pre­dic­tive mod­els” in vogue today. We show that, giv­en a set of hypothe­ses, the solu­tion of an opti­mi­sa­tion prob­lem — find­ing the best tun­ing scheme for all musi­cal works in a reper­toire — is not unique as it depends on ini­tial con­di­tions. Further, the same ini­tial con­di­tions may pro­duce a cloud of seem­ing­ly iden­ti­cal solu­tions, even though each of them points at utter­ly dif­fer­ent pro­ce­dures for its real­i­sa­tion in the “real world” — here, tun­ing a harpsichord.

The give­away mes­sage is that sci­en­tists should not be impressed by the accu­ra­cy and appar­ent con­sis­ten­cy of solu­tions pro­duced by machines. They need to crit­i­cal­ly exam­ine ini­tial con­di­tions and the com­pu­ta­tion­al process itself.

In the end, lis­ten­ing to the audio ren­der­ing of results is the only accept­able way to (in)validate a com­po­si­tion­al model.

“Standard” analysis

The Well-tempered Clavier com­pris­es two books, each enlist­ing 24 pre­ludes and 24 fugues in all con­ven­tion­al key sig­na­tures. In sum, this analy­sis cov­ered 96 musi­cal works (pre­sum­ably) com­posed by the same com­pos­er in (pre­sum­ably) sim­i­lar conditions.

Our first analy­sis relies on the fol­low­ing set­tings of inter­vals esti­mat­ed con­so­nant or dis­so­nant:

Settings for “stan­dard” analysis

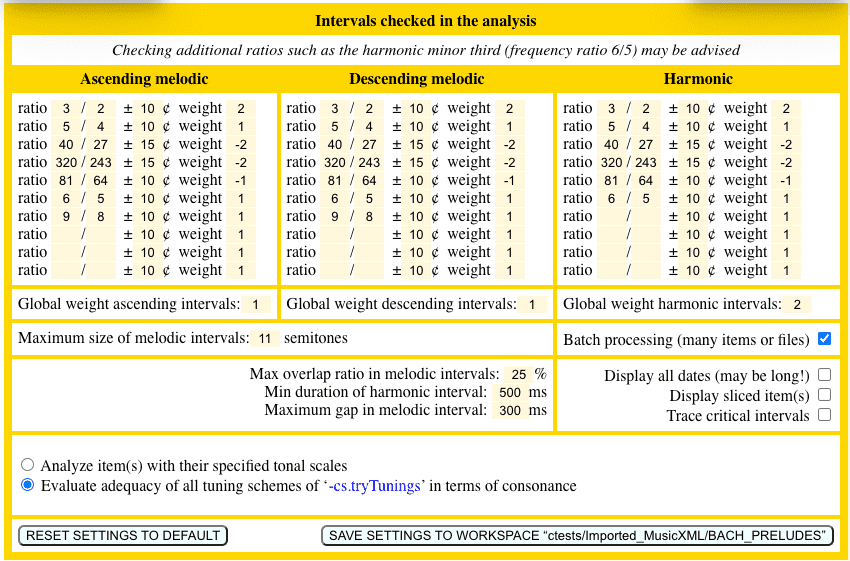
The analy­sis of ascend­ing and descend­ing melod­ic inter­vals checks for com­mon fre­quen­cy ratios close to 3/2 (Pythagorean fifths) and 5/4 (har­mon­ic major thirds) which are wide­ly esti­mat­ed “con­so­nant”. It also includes ratios 6/5 (har­mon­ic minor thirds) and 9/8 (Pythagorean major sec­onds) which may be con­sid­ered opti­mal. Other ratios are often rat­ed “dis­so­nant”: 40/27 (wolf fifth), 320/243 (wolf fourth) and 81/64 (Pythagorean major third). These dis­so­nant inter­vals are 1 com­ma (ratio 81/80) high­er or low­er than their “con­so­nant” neigh­bours — read page Just into­na­tion: a gen­er­al frame­work.

Consonant inter­vals have been assigned pos­i­tive weights, for instance ‘1’ for a har­mon­ic major third and ‘2′ for a Pythagorean fifth. Dissonant inter­vals are assigned neg­a­tive weights, for instance ‘-2′ for wolf inter­vals and ‘-1’ for Pythagorean major thirds. These weights can be mod­i­fied; indeed, the mod­i­fi­ca­tion will in turn alter the rat­ings of tun­ing schemes.

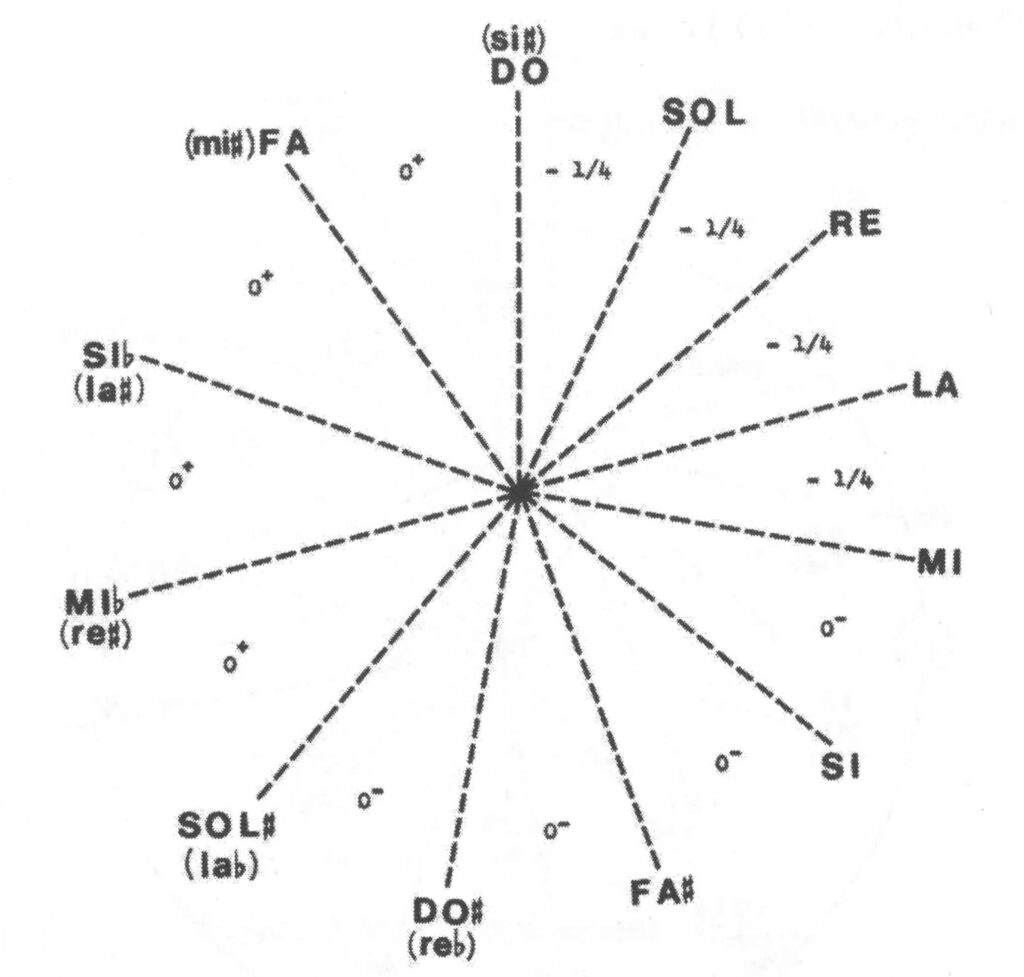
Each melod­ic inter­val found in the musi­cal work will be sized as per the same inter­val in the tonal scale assessed for com­pat­i­bil­i­ty. For instance, when try­ing to match the D’Alambert-Rousseau tun­ing scheme (see image), a note sequence ‘C’ - ‘Eb’ will be sized 290 cents, which is close to 294 cents or ratio 32/27 (Pythagorean minor third). Should this ratio appear in the set­tings, the score of the scale will be incre­ment­ed by the weight of the ratio mul­ti­plied by the (sym­bol­ic) dura­tion of the inter­val — read Tonal analy­sis of musi­cal works for details of this procedure.

The same method is applied to har­mon­ic inter­vals, here assigned the same weights as melod­ic inter­vals, except ratio 9/8 which is ignored.

Scores for ascend­ing and descend­ing melod­ic inter­vals are then added with the score for har­mon­ic inter­vals, with respec­tive weights 1, 1, and 2. This weigh­ing can also be mod­i­fied if “con­so­nance” is more expect­ed on melod­ic ver­sus har­mon­ic inter­vals, or if ascend­ing and descend­ing melod­ic inter­vals are not esti­mat­ed of equal importance.

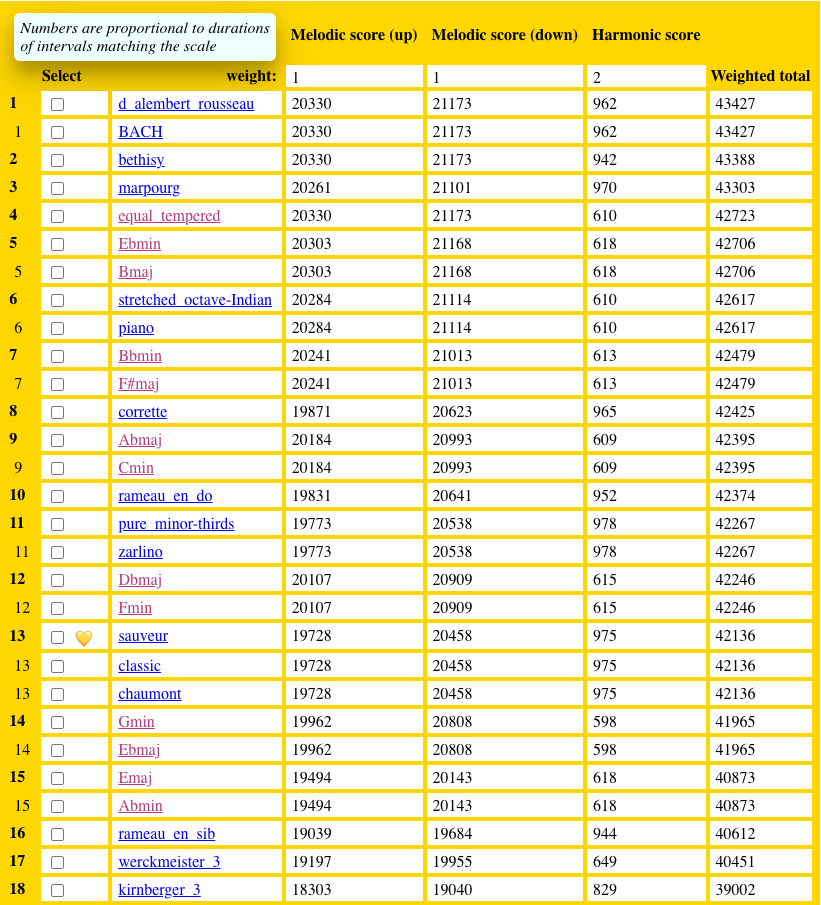
Every tonal scale is grat­i­fied with a mark when found the best match for a musi­cal item. Counting these marks over the whole reper­toire indi­cates the best tun­ing scheme(s) for this repertoire.

Results are stored in tables that can be down­loaded in both HTML and CSV for­mats. The ini­tial set­tings are remind­ed at the bot­tom of the “all results” HTML page.

Each cell in the “all results” table indi­cates the rank of a giv­en tun­ing scheme (scale) matched against a giv­en musi­cal work. For instance, in the fugues of book I, Corette’s tem­pera­ment (col­umn cor­rette) ranked 6th for the 5th fugue, and the best match for this piece was Sauveur’s tem­pera­ment (col­umn sauveur).

The line labelled Ranked first (times) dis­plays the num­ber of times each tun­ing scheme ranked first in the clas­si­fi­ca­tion of this cor­pus. The line labelled Average score dis­plays the aver­age glob­al (melod­ic + har­mon­ic) score com­put­ed for this tun­ing scheme, as explained on our page Tonal analy­sis.

Abstract tables dis­play the list of tun­ing schemes rank­ing first for each musi­cal work.

➡ The com­plete set of scale images is avail­able on this page.

Discussion of the standard analysis

The scale of Sauveur’s temperament

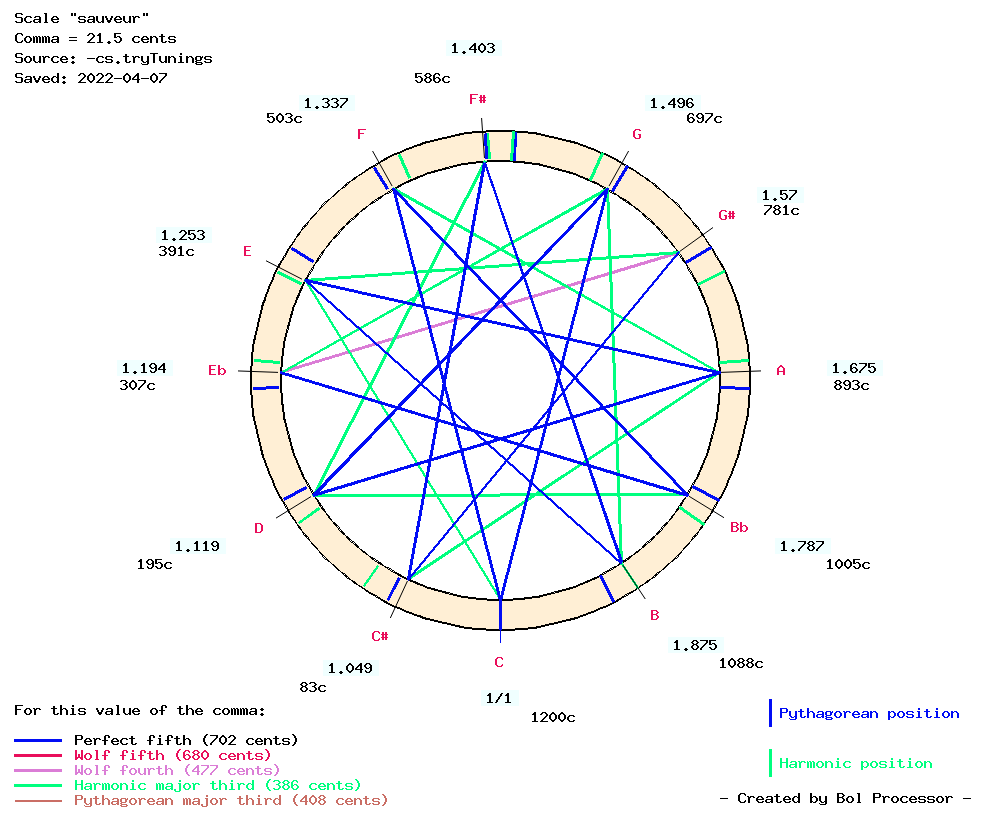
Out of these 96 musi­cal works, 56 opt­ed for ‘sauveur’ as their favourite tun­ing scheme, plus 9 as next to favourite. This tem­pera­ment strik­ing­ly dom­i­nates the clas­si­fi­ca­tion because of its pro­fi­cien­cy in almost per­fect Pythagorean fifths (ratio 3/2), har­mon­ic major thirds (ratio 5/4) and har­mon­ic minor thirds (ratio 6/5).

Note that it also con­tains a wolf fourth ‘Eb’ - ‘G#’ close to 477 cents (or ratio 320/243) per­ceived as a dis­so­nant inter­val. The guess is that these two notes are nev­er (or rarely) found in melod­ic or har­mon­ic inter­vals on this reper­toire. This illus­trates the fact that there no one-fits-all solu­tion to the prob­lem of tun­ing an instru­ment for this type of music. In a “reverse engi­neer­ing” turn of mind, we may say that the com­pos­er explored melod­ic and har­mon­ic pleas­ant effects to build this reper­toire: play­ing on the instru­ment before notat­ing on sheets of musi­cal scores.

As sug­gest­ed in our tuto­r­i­al, there is no evi­dence of J.S. Bach’s aware­ness of the the­o­ret­i­cal work by French physi­cian Joseph Sauveur, but the the­o­ret­i­cal frame­work of this tem­pera­ment — a sin­gle sequence of fifths dimin­ished by 1/5 com­ma (see image and read Asselin, 2000 p. 80) — sug­gests that any com­pos­er might fig­ure it out inde­pen­dent­ly. This process has been record­ed as fol­lows on Bol Processor’s Scale page:

Created meantone downward notes “do,fa,sib,mib” fraction 3/2 adjusted -1/5 comma
Created meantone upward notes “do,sol,re,la,mi,si,fa#,do#,sol#” fraction 3/2 adjusted -1/5 comma

Interestingly, “nat­ur­al scales” with names equat­ing the key — for instance Abmin (i.e. G#min) for the Fugue 18 in G♯ minor, book II (BWV 887) — often came on top of the favourite tun­ing schemes, yet in most cas­es out­raced by sev­er­al tem­pera­ments. Read our page Creation of just-intonation scales for more details on these scales.

In all cas­es, the scor­ing of equal-temperament (see image) was among the low­est due to its use of major and minor thirds close to Pythagorean. This con­tra­dicts the pop­u­lar belief that Bach’s series of pre­ludes and fugues aimed at equat­ing “well-tempered” with “equal-tempered”…

This first result also sug­gests that tem­pera­ments often pro­vide a bet­ter tonal struc­ture for achiev­ing max­i­mum con­so­nance than the so-called just into­na­tion scales.

Temperaments are based on empir­i­cal tun­ing pro­ce­dures guid­ed by per­ceived inter­vals (read Asselin, 2000) where­as “just into­na­tion” is the out­come of spec­u­la­tions on num­ber ratios — a deduc­tive process. This takes us back to a dis­cus­sion of the ancient Indian approach of tonal­i­ty, read page The two-vina exper­i­ment.

“Alternate” analysis

At this stage, it is tempt­ing to con­clude that J.S. Bach’s The Well-Tempered Clavier was meant to be per­formed on instru­ments tuned as per Sauveur’s tem­pera­ment. However, the result of an analy­sis always need to be exam­ined for bias­es in its hypothe­ses. In the present case, we need to revise the choice of cer­tain fre­quen­cy ratios as cri­te­ria for eval­u­at­ing the “con­so­nance” of melod­ic and har­mon­ic intervals.

The minor third — either har­mon­ic (6/5) or Pythagorean (32/27) — is at stake because the Pythagorean minor third appears in some tem­pera­ments. For instance, the Cmaj nat­ur­al scale (see image) uses 32/27 for its inter­val ‘C’ - ‘Eb’. Therefore, it makes sense to ignore all minor thirds in the eval­u­a­tion of har­mon­ic inter­vals and accept both ratios 6/5 and 32/27 with equal pos­i­tive weights in melod­ic inter­vals. This option will be illus­trat­ed by sound exam­ples, read fur­ther. A mean­ing­ful vari­ant would be dif­fer­ent ratios in ascend­ing and descend­ing har­mon­ic intervals.

Same remark regard­ing major thirds: even though ratio 5/4 (har­mon­ic) sounds cer­tain­ly bet­ter than 81/64 (Pythagorean) in har­mon­ic inter­vals, there is no strong rea­son to pre­fer the for­mer in melod­ic inter­vals — again with a pos­si­ble dis­tinc­tion between ascend­ing and descend­ing movements.

Let us start again the entire analy­sis with these mod­i­fied settings:

Settings for “alter­nate” analysis

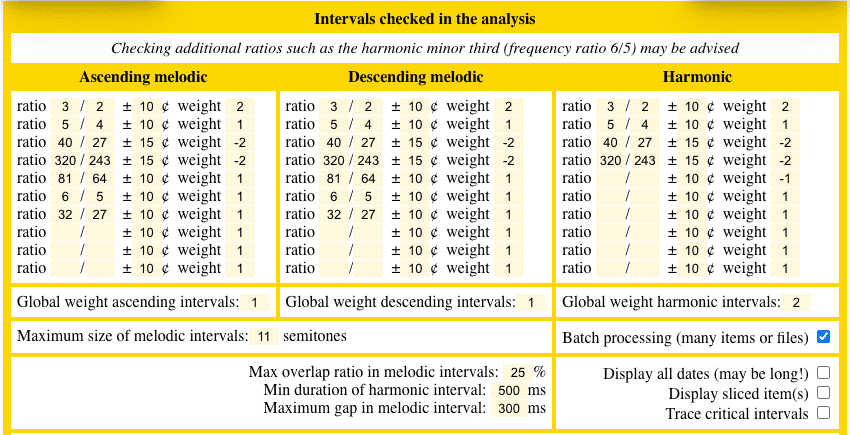
Results are the following:

Discussion of the alternate analysis

Results con­tra­dict the con­clu­sion of the “stan­dard” analy­sis: Sauveur’s tem­pera­ment might not be such a good choice, giv­en the alter­nate choice of ratios for consonant/dissonant melod­ic and har­mon­ic intervals.

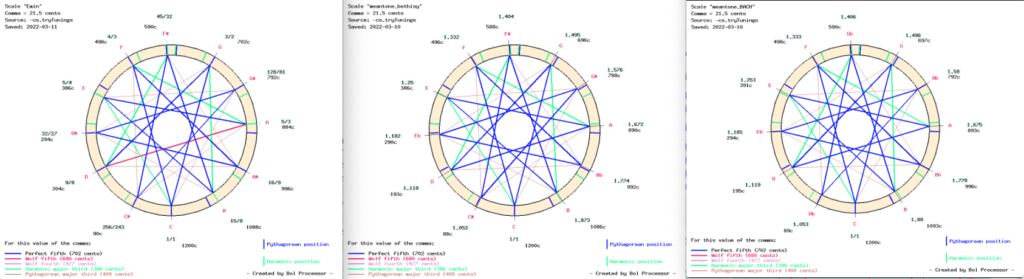
According to these set­tings, the best tun­ing schemes might be D’Alambert-Rousseau tem­pera­ment (see image and read Asselin, 2000 p. 119) and H.A. Kellner’s BACH tem­pera­ment (see image and read Asselin, 2000 p. 101). Both have been designed after J.S. Bach’s death, but sim­i­lar or iden­ti­cal tun­ing pro­ce­dures could be fig­ured out by the composer.

Comparing the images and cent posi­tions (equal with­in ± 7 cents) explains why these two tem­pera­ments pro­duced iden­ti­cal match­es despite their utter­ly dif­fer­ent tun­ing pro­ce­dures. Look at the pro­ce­dures (traced by the algo­rithm) and lis­ten to short note sequences pro­duced with these scales:

D'Alembert-Rousseau temperament
Created meantone upward notes “do,sol,re,la,mi” fraction 3/2 adjusted -1/4 comma
Created meantone downward notes “do,fa,sib,mib,sol#” fraction 3/2 adjusted 1/12 comma
Equalized intervals over series “sol#,do#,fa#,si,mi” approx fraction 2/3 adjusted 2.2 cents to ratio = 0.668

Sequence of notes accord­ing to D’Alembert-Rousseau temperament

Kellner's BACH temperament
Created meantone upward notes “do,sol,re,la,mi” fraction 3/2 adjusted -1/5 comma
Added fifths down: “do,fa,sib,mib,lab,reb,solb” starting fraction 1/1
Created meantone upward notes “mi,si” fraction 3/2

Sequence of notes accord­ing to Kellner’s BACH temperament

As a reminder, the same sequence of notes with an equal-tempered scale:

Sequence of notes accord­ing to equal temperament
D’Alembert-Rousseau tun­ing scheme (Asselin, 2000 p. 119)

These tun­ing pro­ce­dures do not repro­duce pre­cise­ly the ones described by Asselin (2000 p. 120 and 102) but they yield the same tonal positions.

In these tem­pera­ments, inter­vals such as ‘C’ - ‘Eb’ are ren­dered as Pythagorean minor thirds (32/27), and many Pythagorean major thirds (ratio 81/64) are encoun­tered. This jus­ti­fies their choice, giv­en the new con­di­tions of analysis.

Again, these tem­pera­ments dom­i­nate the clas­si­fi­ca­tion, rank­ing 65 times in first posi­tion and 15 times in sec­ond posi­tion, where­as equal-temperament ranked first only 21 times despite its pro­fi­cien­cy in Pythagorean major thirds. Compared with Sauveur’s tem­pera­ment in the stan­dard analy­sis (56 first posi­tions and 9 sec­ond posi­tions) these tun­ing schemes look “bet­ter”, yet this com­par­i­son is irrel­e­vant since the two analy­ses focussed on dif­fer­ent ratios.

The 33 pre­ludes and fugues uncom­pli­ant with these tem­pera­ments often pre­ferred a just-intonation scale in the same key, for instance Prelude 8 in E♭ minor of book I (BWV 853) selects the Ebmin scale, and Prelude 9 in E major of book I (BWV 854) selects the Emaj scale. However, this match­ing is less fre­quent in “dis­si­dent” fugues.

More advanced analy­ses are required. Keep in mind that chang­ing the weights of inter­vals or weights in the sum­ming of melod­ic and har­mon­ic scores may rad­i­cal­ly mod­i­fy the classification.

In this dis­cus­sion, we only exam­ined tun­ing schemes at the top of the clas­si­fi­ca­tion. Other schemes may be prefer­able when look­ing sep­a­rate­ly at melod­ic or har­mon­ic scores — read our tuto­r­i­al Tonal analy­sis.

Sound examples

The auto­mat­ic tonal analy­sis of a large reper­toire matched against the whole set of tun­ing schemes imple­ment­ed in the Bol Processor did not solve the prob­lem of find­ing “the best tun­ing scheme” for this reper­toire, as it depends on ini­tial con­di­tions: fre­quen­cy ratios esti­mat­ed “con­so­nant” or “dis­so­nant”, plus the com­poser’s pre­sumed focus on opti­mal con­so­nance. Nonetheless, two analy­ses select­ed 2 (or 3) tun­ing schemes as dom­i­nant in the clas­si­fi­ca­tion. More analy­ses would be required to refine this result, if of any significance.

All sound exam­ples are found, com­pared with human inter­pre­ta­tions play­ing (not so well-tempered ?) phys­i­cal instru­ments, on page The Well-tempered clavier.

These sound exam­ples are use­ful to hear the dif­fer­ence between tun­ing schemes select­ed on the basis of the “stan­dard” and “alter­nate” set­tings. For exam­ple, Fugue 8 of book I may sound more tune­ful with a Dmin tun­ing (see image) than with Marpurg (see image). The dif­fer­ence might reside in the choice of con­ve­nient ratios for minor thirds.

Is this method reliable?

As sug­gest­ed by results dis­played in the 4 tables for each book (see above), a few pre­ludes and fugues ranked sev­er­al tun­ing schemes as their favourite ones: num­ber ‘1′ coloured red in “all results” tables. Despite this, we pro­duced record­ings for only one of the win­ners. How far does this matter?

Take for exam­ple Prelude 12 of book I. In “alter­nate” set­tings, five scales ranked first: Emin, Cmaj, BACH, d_alembert_rousseau, bethisy. We already showed that BACH and d_alembert_rousseau are almost iden­ti­cal despite dif­fer­ences in their tun­ing pro­ce­dures. Emin and Cmaj are strict­ly iden­ti­cal. This leaves us with the fol­low­ing choice:

Three scales rank­ing 1st for Prelude 12 of book 1 as per “alter­nate” settings

Tonal posi­tions only dif­fer by a few cents, which may not be noticed in melod­ic and har­mon­ic inter­vals. Below are record­ings using these three scales:

Prelude 12 of book I, Emin tun­ing scheme
Prelude 12 of book I, Bethisy temperament
Prelude 12 of book I, Kellner’s BACH temperament

This exam­ple sug­gests that dif­fer­ences in scales rank­ing first may be inaudi­ble if the widths of accept­able melod­ic and har­mon­ic inter­vals have been set small enough to pro­vide a well-focussed solu­tion set. 

Listen to minor thirds

Appreciating by ear the sizes of com­mon minor thirds may clar­i­fy the point of decid­ing which one is more “con­so­nant”. Lucky users of Bol Processor BP3 only need to cre­ate the fol­low­ing data file:

-cs.tryTunings

// Harmonic minor third
_scale(2_cycles_of_fifths,0) DO3 RE#3 DO3 RE#3 DO3 RE#3 {4,DO3,RE#3}

//Pythagorean minor third
_scale(2_cycles_of_fifths,0) DO3 MIb=RE#-c3 DO3 MIb=RE#-c3 DO3 MIb=RE#-c3 {4,DO3,MIb=RE#-c3}

// Sequence harmonic then pythagorean
_scale(2_cycles_of_fifths,0) DO3 RE#3 DO3 MIb=RE#-c3 DO3 RE#3 DO3 MIb=RE#-c3 -{2,DO3,RE#3} {2,DO3,MIb=RE#-c3} {2,DO3,RE#3} {2,DO3,MIb=RE#-c3} {2,DO3,RE#3} {2,DO3,MIb=RE#-c3}

These items pro­duce sequences of ‘C’ - ‘D#’ melod­ic and har­mon­ic inter­vals using har­mon­ic (6/5) and Pythagorean (32/27) minor thirds:

Harmonic minor thirds in sequence then superposed
Pythagorean minor thirds in sequence then superposed
Alternance of har­mon­ic then Pythagorean minor thirds

Listening to these exam­ples sug­gests that both 6/5 and 32/27 are eli­gi­ble ratios for minor thirds as “con­so­nant” melod­ic inter­vals, where­as 6/5 sounds “soft­er” than 32/27 as a har­mon­ic interval.

The “2_cycles_of_fifths” scale

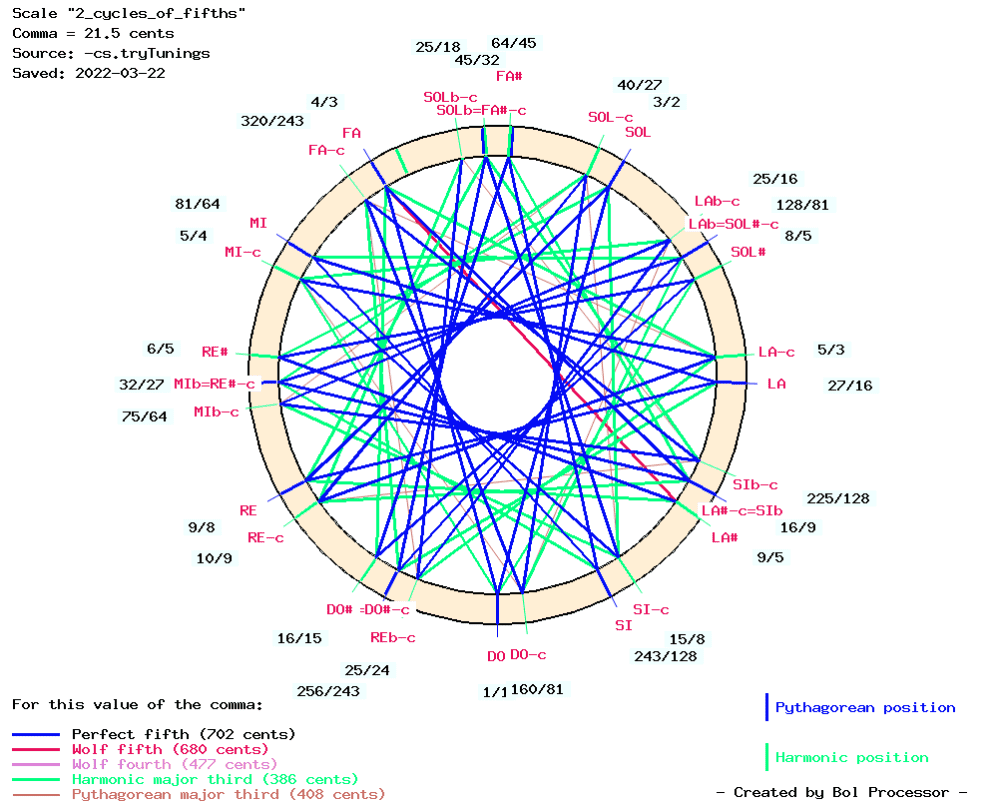
This demo makes use of scale “2_cycles_of_fifths” described by Asselin (2000, p. 62) and imple­ment­ed on a Scale page of Bol Processor — read pages Microtonality and Just into­na­tion: a gen­er­al frame­work.

The names of notes (inspired by the book, ibid.) sound bizarre but they make posi­tions explic­it. For instance, “Mib=RE#-c” indi­cates a posi­tion that is usu­al­ly called mi bémol (E flat) and iden­ti­cal to ré dièse (D sharp) minus one comma.

This scale — and the even more com­pli­cat­ed “3_cycles_of_fifths” — is not prac­ti­cal to write music… It is used to visu­alise (and hear) tonal posi­tions cre­at­ed by var­i­ous tun­ing schemes com­pli­ant with the just into­na­tion paradigm.

Listen to tempered fifths

Readers unfa­mil­iar with tun­ing pro­ce­dures may need to appre­ci­ate tiny dif­fer­ences in inter­vals pro­duced by tem­pera­ments cre­at­ed with the meth­ods intro­duced on page Microtonality and ful­ly described in Asselin (2000).

Let us lis­ten to Pythagorean fifths in three forms: pure (fre­quen­cy ratio 3/2 = 702 cents), equal-tempered (700 cents), dimin­ished by 1/5 com­ma (697.3 cents) and dimin­ished by 1/4 com­ma (696.2 cents).

Pure fifth (702 cents)
Equal-tempered fifth (700 cents)
Fifth dimin­ished by 1/5 com­ma (697.3 cents)
Fifth dimin­ished by 1/4 com­ma (696.2 cents)
Sequence of fifths: pure, then equal-tempered, then dimin­ished by 1/5 com­ma, then dimin­ished by 1/4 comma

Below is the Csound score of the last example:

i1 0.000 4.000 261.630 90.000 90.000 0.000 0.000 0.000 0.000 ; do4
i1 0.000 4.000 392.445 90.000 90.000 0.000 0.000 0.000 0.000 ; sol4
i1 4.000 4.000 261.626 90.000 90.000 0.000 0.000 0.000 0.000 ; C4
i1 4.000 4.000 391.996 90.000 90.000 0.000 0.000 0.000 0.000 ; G4
i1 8.000 4.000 261.630 90.000 90.000 0.000 0.000 0.000 0.000 ; do4
i1 8.000 4.000 391.399 90.000 90.000 0.000 0.000 0.000 0.000 ; sol-1|5c4
i1 12.000 4.000 261.630 90.000 90.000 0.000 0.000 0.000 0.000 ; do4
i1 12.000 4.000 391.137 90.000 90.000 0.000 0.000 0.000 0.000 ; sol-1|4c4

Goldberg Variations

The same exer­cise has been tried on J.S. Bach’s Goldberg Variations (1741). The aria and its thir­ty vari­a­tions were per­formed in a sin­gle sequence, obvi­ous­ly with the same instrument/tuning. For this rea­son, we checked a unique MusicXML score con­tain­ing all variations.

With the “stan­dard” hypoth­e­sis of con­so­nance, the result is the following:

(As expect­ed) Sauveur’s mean­tone tem­pera­ment won the game, fol­lowed with Kellner’s BACH. The equal-tempered scale ranked 28th on this clas­si­fi­ca­tion… (Note that the com­pu­ta­tion of this table took 3 1/2 hours on an old MacBook Pro…).

Listen to the syn­the­sis of Goldberg Variations with Sauveur’s mean­tone temperament:

The “alter­nate” mod­el of con­so­nance yields the fol­low­ing classification:

Favourite tun­ing schemes, accord­ing to this mod­el, would be D’Alembert-Rousseau (see image) and Kellner’s BACH (see image) mean­tone tem­pera­ments, both with equal rat­ings since their tonal inter­vals are almost identical.

Listen to the syn­the­sis of Goldberg Variations with D’Alembert-Rousseau temperament:

Source: Wikipedia

These favourite tun­ings are the same ones best fit to the set of pre­ludes and fugues in The Well-tempered Clavier.

These sound exam­ples may be com­pared with human per­for­mances, for exam­ple the Aria on a harp­si­chord tuned with Werckmeister III mean­tone tem­pera­ment — lis­ten to this record­ing. Indeed, musi­cians dis­play a more flex­i­ble tim­ing com­pared with Bol Processor stick­ing to para­me­ters of the MusicXML score. Nonetheless, a com­par­i­son focussing on tonal inter­vals remains possible.

The fact that Werckmeister III (see image) ranked low in the auto­mat­ic tonal analy­sis does not sug­gest an improp­er choice. This tun­ing scheme might rank high­er against a spe­cif­ic mod­el of “con­so­nance”.

Let us fig­ure out with cal­cu­la­tions its main dif­fer­ence with D’Alembert-Rousseau and Kellner’s BACH. We may restrict the analy­sis to mea­sures #1 to #32 (the Aria) expos­ing most melodic/harmonic inter­vals; this Aria works sim­i­lar to the ini­tial sec­tion (ālāp) in North Indian clas­si­cal music… We notice that nei­ther D - F# (397 cents) nor G - B (398 cents) in Werckmeister III are accu­rate har­mon­ic major thirds (390 cents), inter­vals with high occur­rence as shown on the table of inter­val frequencies:

Interval fre­quen­cies in the Aria of Goldberg Variations

The fol­low­ing is a com­par­i­son of scales Werckmeister III and D’Alembert-Rousseau in terms of match­ing melod­ic inter­vals (in the “alter­nate” mod­el of con­so­nance) over the 32 first mea­sures of Goldberg Variations:

Matching two scales with the melod­ic inter­vals of the Aria in Goldberg Variations:
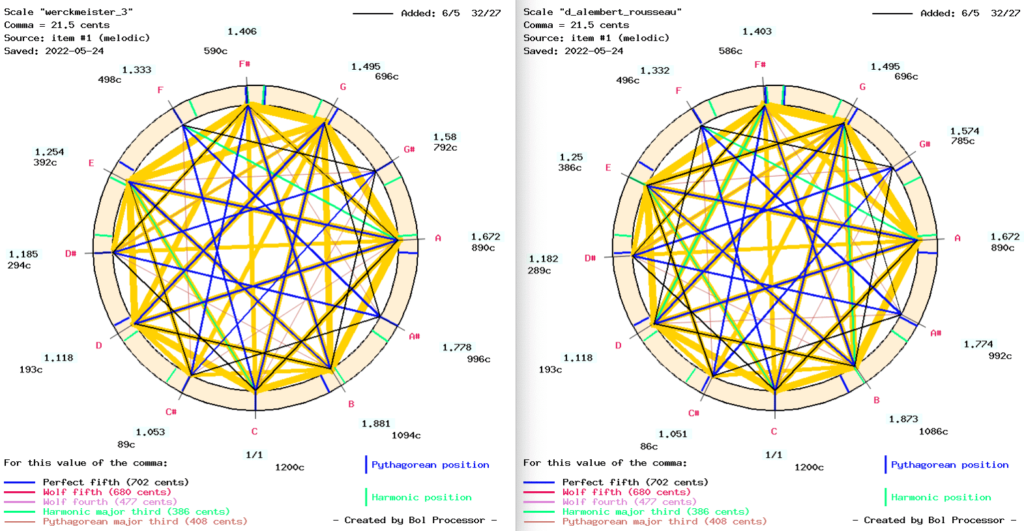
Werckmeister III (left) and D’Alembert-Rousseau (right)

The widths of yel­low lines are pro­por­tion­al to the occurrence/durations of melod­ic inter­vals in this part of the cor­pus. The pic­ture con­firms the absence of an accu­rate har­mon­ic major third D - F# in the Werckmeister III scale, and the same mis­match of major third G - B. Another mis­match is on minor third E - G, here aim­ing at ratio 6/5 (315 cents) or 32/27 (294 cents).

Sources of MusicXML scores

Links point at MusicXML scores used for this analy­sis. These links must be men­tioned in the attri­bu­tion part of Creative Commons licences. Upgraded ver­sions are welcome.

Our thanks to edi­tors of these scores in the MuseScore community!

The (pub­lic domain) score of Goldberg Variations has been edit­ed by MuseScore lead devel­op­er Werner Schweer.

Book I sources

1BWV 846CmajPreludeFugue
2BWV 847CminPreludeFugue
3BWV 848C#majPreludeFugue
4BWV 849C#minPreludeFugue
5BWV 850DmajPreludeFugue
6BWV 851DminPreludeFugue
7BWV 852E♭majPreludeFugue
8BWV 853E♭min/D#minPreludeFugue
9BWV 854EmajPreludeFugue
10BWV 855EminPreludeFugue
11BWV 856FmajPreludeFugue
12BWV 857FminPreludeFugue
13BWV 858F#majPreludeFugue
14BWV 859F#minPreludeFugue
15BWV 860GmajPreludeFugue
16BWV 861GminPreludeFugue
17BWV 862A♭majPreludeFugue
18BWV 863G#minPreludeFugue
19BWV 864AmajPreludeFugue
20BWV 865AminPreludeFugue
21BWV 866B♭majPreludeFugue
22BWV 867B♭minPreludeFugue
23BWV 868BmajPreludeFugue
24BWV 869BminPreludeFugue

Book II sources

1BWV 870CmajPreludeFugue
2BWV 871CminPreludeFugue
3BWV 872C#majPreludeFugue
4BWV 873C#minPreludeFugue
5BWV 874DmajPreludeFugue
6BWV 875DminPreludeFugue
7BWV 876E♭majPreludeFugue
8BWV 877D#minPreludeFugue
9BWV 878EmajPreludeFugue
10BWV 879EminPreludeFugue
11BWV 880FmajPreludeFugue
12BWV 881FminPreludeFugue
13BWV 882F#majPreludeFugue
14BWV 883F#minPreludeFugue
15BWV 884GmajPreludeFugue
16BWV 885GminPreludeFugue
17BWV 886A♭majPreludeFugue
18BWV 887G#minPreludeFugue
19BWV 888AmajPreludeFugue
20BWV 889AminPreludeFugue
21BWV 890B♭majPreludeFugue
22BWV 891B♭minPreludeFugue
23BWV 892BmajPreludeFugue
24BWV 893BminPreludeFugue

Reference(s)

Asselin, P.-Y. Musique et tem­péra­ment. Paris, 1985, repub­lished in 2000: Jobert. Soon avail­able in English.

Leave a Reply

Your email address will not be published. Required fields are marked *