Polymetric expressions are the basic representation model for the timing of musical data in the Bol Processor. The word is a mixture of polyphony and polyrhythm, the former evoking superimposed streams of musical events, and the latter a metric adjustment of their durations.
This page illustrates the syntax of simple expressions and their interpretation by the polymetric expansion algorithm described in Two algorithms for the instantiation of structures of musical objects (Bel 1992). This process can be extremely complex, since an entire musical work — e.g. Beethoven's Fugue in B flat major — is treated by the Bol Processor as a single polymetric structure.
In this tutorial, simple notes ("C4", "D4" etc.) are used following the "English" convention. All time-setting processes could be illustrated using sound-objects or simple notes in other conventions: "Italian/Spanish/French" or "Indian".
Symbolic versus physical duration
Music notation systems (for humans) make use of symbolic rather than physical durations. Their units are beats rather than (milli)seconds.

in western conventional music notation
In western conventional music notation, notes and pauses are represented by special signs indicating their relative durations.
For example, if the time signature is 3/4, we will have 3 quarter notes (crotchets) in a bar (see picture). A half note (minim) lasts twice as long as a quarter note in the same context. Other relative durations are expressed in the same way.
To get the physical duration of a note we need an additional piece of information: the metronome value, for example "mm = 100", which means 100 beats (quarter notes) per minute.
A metronome value (60 bpm by default ) is declared in the settings file of a Grammar or Data page. With this setting, note "E4" on a Bol Processor score represents an "E" of the 4th octave played in 1 beat with a physical duration of 1 second.
This convention extends to arbitrarily named sound-objects whose default durations are set by the streams of MIDI events or sequences of Csound instructions from which they are composed. The mapping of symbolic to physical time for the performance of sound-object structures (with their metric and topological properties) is a sophisticated process performed by a time-setting algorithm. A practical example is discussed on the page Interactive improvisation with sound-objects.
Polymetric expression
Typical forms of polymetric expressions are:
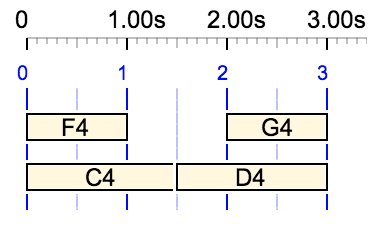
- field 1, field2 or {field 1, field2} indicates that field1 and field2 should be superimposed and the total symbolic duration should be adjusted to that of field1;
- field1 • field2 or {field1 • field2} indicates that field1 and field2 should be consecutive and the symbolic duration of each field should be adjusted to that of field1;
- {expression} is equivalent to expression.
Curly braces '{' and '}' are used to create multi-level expressions.
➡ Periods written as bullets '•' in the Data and Grammar windows are converted to plain periods before being sent to the console, as the console rejects some Unicode characters.
For example, {C4 D4, E4 F4 G4, E5} produces the following time structure with a metronome set to 60 beats per minute:
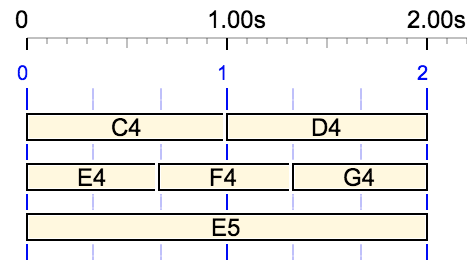
The duration is 2 beats, as set by the first field "C4 D4"
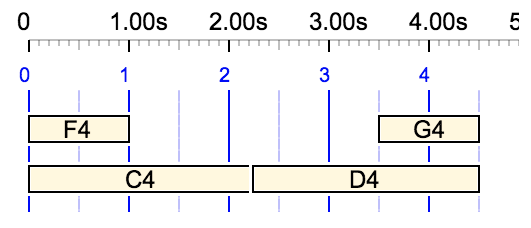
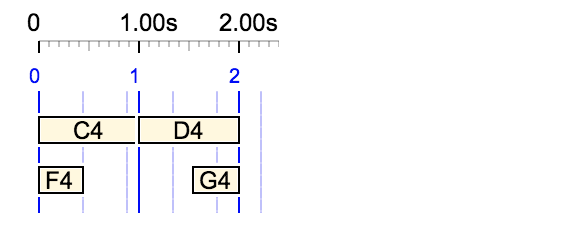
The use of the first field to set the total duration is highlighted by the following examples where the fields appear in a reverse order:
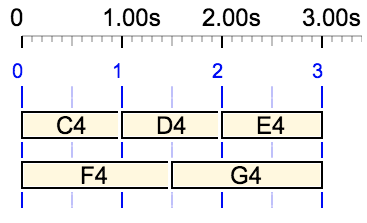
Duration of 3 beats
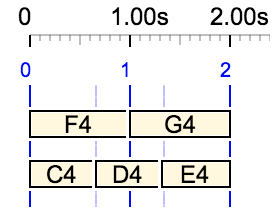
Duration of 2 beats
Rests (silences) can be notated with "-" for single unit rests, or with integer numbers and ratios. The following shows a single unit rest and a more complex rest of 2.5 beats:
Duration of 3 beats
Duration of 4.5 beats
Duration of 2 beats
Polymetric structures can be multi-level, for example:
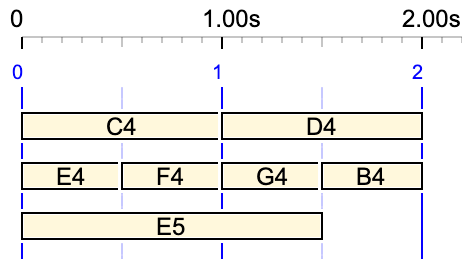
{C4 D4, {E4 F4 G4, E5} B4}
The same time-setting rules apply to sequences where commas are replaced by periods. For example:

Duration is set by that of the first field "F4 2 1/2 G4"
= 4.5 beats applied to the second field
Superpositions and sequences can be combined (even in multi-level expressions), such as:
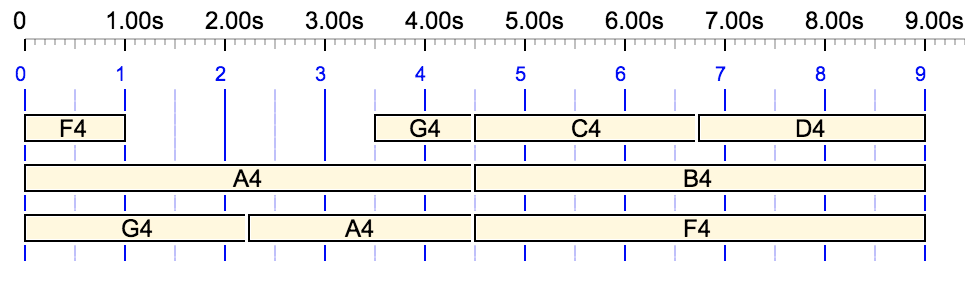
Duration of 9 beats = twice that of "F4 2 1/2 G4"
Undetermined rests
Undetermined rests are a powerful feature of polymetric expressions used to avoid inconvenient computations. The polymetric expansion algorithm calculates (symbolic) durations that produce the least complex expression.
They may be notated as "…" or "_rest" in Data or Grammars.
➡ Since the console does not recognise the "…" Unicode symbol, the PHP interface rewrites it as"_rest".
Let us start with a trivial example. In {C4 D4 E4, … F4 G4}, the undetermined rest "…" is replaced by a single unit rest:
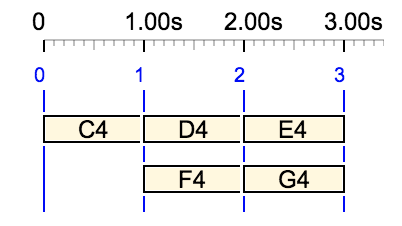
= {C4 D4 E4, _rest F4 G4}
This solution gives the simplest polymetric expression. The same simple case is that of {… C4 D4 E4, F4 G4}:
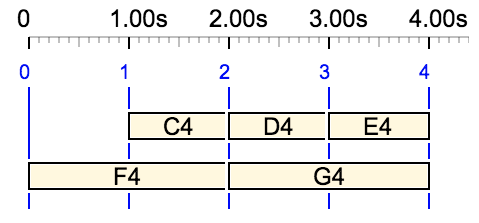
= {_rest C4 D4 E4, F4 G4}
If a field of the polymetric expression contains several undetermined rests, these are assigned equal durations — in such a way that the complexity of the structure remains minimal. For example, consider {… C4 D4 … E4, A4 F4 G4}:
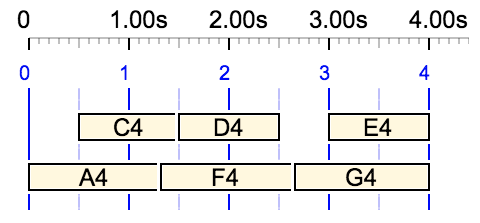
= {_rest C4 D4 _rest E4, A4 F4 G4}
An undetermined rest may even be assigned duration 0 in case this yields a simpler expression. For example, in {… C4 D4 … E4, F4 G4} duration 0 gives a "three in two" polyrhythm whereas duration 1 would give "five in two". The criterion for evaluating the complexity is to get the lowest common multiple (LCM) of the number of units in each field, in fact 6 against 10. Therefore the solution is:
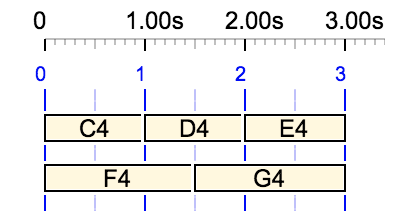
Each field of a polymetric expression can contain undetermined rests. Consider for example {… C4 D4 E4, A4 B4 F4 … G4}. Again, assigning a duration of zero to each undetermined rest gives the simplest structure, since "four in three" (LCM = 12) is a better trade-off than "five in four" (LCM = 20).
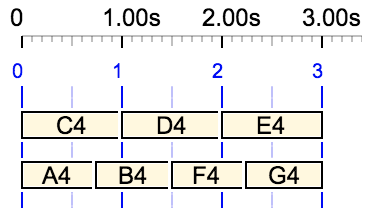
A more complex structure is assigned to {C4 D4 E4, A4 B4 F4 … G4 A4, C5 … D5} with rests of 1 unit in the second and third fields. The LCM of 3 and 6 is 6, which is the lowest value possible for this structure.
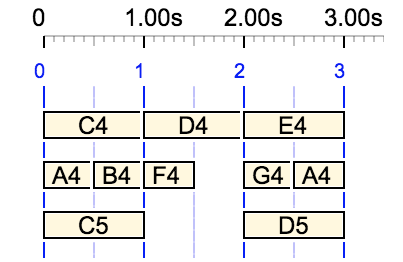
Note that there is an equivalent solution in terms of complexity: assigning duration 0 to the rest in the third field. If more than one solution is valid, the algorithm chooses the one with the fewest zero-duration rests.
A similar case is {C4 D4 E4, A4 B4 F4 … G4 A4, C5 … D5 E5}:
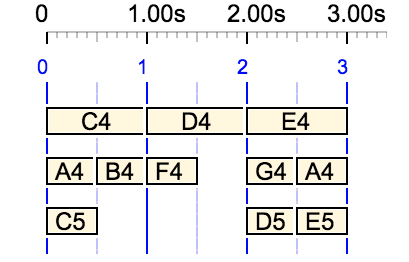
Here, the first rest has been assigned 1 unit and the second one 3 units. This gives the LCM of 3 and 6 = 6. Another optimal (equivalent) solution would be to assign 0 to the second rest, but this was discarded due to the heuristic of avoiding zero duration rests.
Replacing commas with periods gives the same structure in a sequential form:

= {C4 D4 E4 • A4 B4 F4 … G4 A4 • C5 … D5 E5}
Duration of the first field "C4 D4 E4" is applied to the 2nd and 3d ones
which makes a final count of 3 x 3 = 9 beats
Tied notes, tied sound-objects
Sound-objects or simple notes can be concatenated ("tied"). Consider, for example:
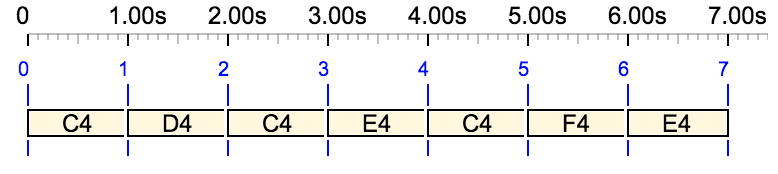
and its variation with ties notated "&":
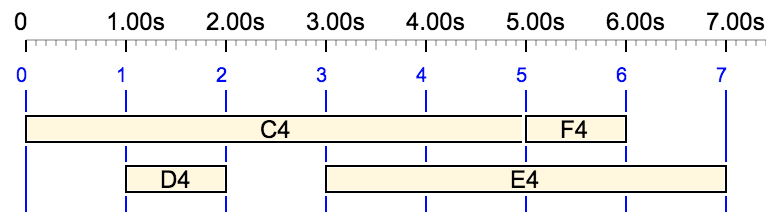
The time interval of a tied note/sound-object may cross the limits of (tree-shaped) polymetric structures. For example:
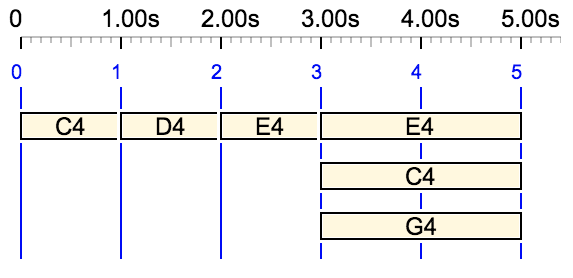
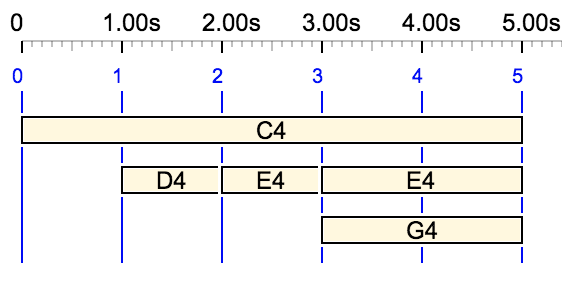
The challenge of dealing with tied events is discussed on the Tied notes page.
Real music is "polymetric"
The rules and heuristics associated with polymetric expressions make sense when dealing with real musical items. In particular, they made it possible to import MusicXML scores and interpret them as Bol Processor data (read page).
For example, check out Mozart’s musical dice game, this "Charles Ames" example and Harm Visser's demos.
Further reading
Bel, Bernard. Rationalizing musical time: syntactic and symbolic-numeric approaches. In Barlow, Clarence (ed.) The Ratio Book. Den Haag: Royal Conservatory - Institute of Sonology. 2001: 86-101.
Bol Processor shares a few features, with respect to pattern representation, with the TIDAL Pattern Language for the Live Encoding of Music (Alex McLean & Geraint Wiggins, 2010).
An Indian conception of time can be seen most clearly in the venerable Bol Processor system for algorithmic music, created by computer scientist Bernard Bel from work on notating tabla rhythms and developed over forty years. Drawing from Indian classical music, it includes an expressive approach to time setting that seems unique to the algorithmic music field, in which sound events are organized in terms of interrelationships before being mapped to physical time. Although not a live coding system itself, it has been heavily influential on the design of the TidalCycles system, particularly its embedded “mininotation” language for describing rhythm in the Bol Processor and more generally its representation of music based not on the duration of events (as in staff notation) but on the duration of cycles.
Alan Blackwell, Emma Cocker, Geoff Cox, Thor Magnusson, Alex McLean, Live Coding: A User's Manual, MIT 2022, page 195.