The first six chapters of Natya Shastra, a Sanskrit treatise on music, dance and drama dating from between 400 BCE and 200 CE, contain the premises of a scale theory that has long attracted the attention of scholars in India and the West. Early interpretations by Western musicologists followed the “discovery” of the text in 1794 by the philologist William Jones. Hermann Helmholtz’s theory of “natural consonance” gave way to many comparative speculations based on phenomena that Indian authors had earlier observed as inherent in the “self-production” (svayambhū) of musical notes (Iyengar 2017 p. 8).
Suvarnalata Rao and Wim van der Meer (2009) published a detailed account of attempts to elucidate the ancient theory of musical scales in the musicological literature, returning to the notions of ṣruti and swara which have changed over time up to present-day musical practice.

In the second half of the 20th century, experimental work with frequency meters led to contradictory conclusions from the analysis of small samples of musical performances. It was only after 1981 that systematic experiments were carried out in India by the ISTAR team (E.J. Arnold, B. Bel, J. Bor and W. van der Meer) with an electronically programmable harmonium (the Shruti Harmonium) and later with a “microscope” for melodic music, the Melodic Movement Analyser (MMA) (Arnold & Bel 1983, Bel & Bor I985), which fed precise pitch data into a computer to process hours of music selected from historical recordings.
After several years of experimental work, it had become clear that although the intonation of Indian classical music is far from being a random process, it would be dangerous to judge an interpretation of the ancient scale theory on the basis of today’s musical data. There are at least three reasons for this:
- There are an infinite number of valid interpretations of the ancient theory, as we will show.
- The concept of raga, the basic principle of Indian classical music, first appeared in literature around 900 CE in Matanga’s Brihaddeshi and underwent gradual development until the 13th century, when Sharangadeva listed 264 ragas in his Sangitratnakara.
- Drones were (probably) not in use at the time of Natya Shastra; the influence of the drone on intonation is considerable, if not dominant, in contemporary music performance.
The ancient Indian theory of scales remains useful for its insight into early melodic classification (the jāti system), which may later have given rise to the raga system. It is therefore best thought of as a topological description of tonal structures. Read Raga Intonation for a more detailed account of theoretical and practical issues.
The subject of this page is an interpretation of the experiment of the two vinas described in Chapter XXVIII.24 of the Natya Shastra. An analysis of the underlying model has been published in A Mathematical Discussion of the Ancient Theory of Scales according to Natyashastra (Bel 1988) which the following presentation will make more comprehensive.
The historical context
Bharata Muni, the author(s) of the Natya Shastra, may have heard of the theories of musical scales attributed to the “ancient Greeks”. At any rate, Indian scholars were able to borrow these models and extend them considerably because of their real knowledge of arithmetic.
Readers of C.K. Raju — especially his excellent Cultural Foundations of Mathematics (2007) — know that Indian mathematicians/philosophers are not only famous for inventing positional notation which took six centuries to be adopted in Europe… They also laid out the foundations of calculus and infinitesimals, which were later exported to Europe by Jesuit priests from Kerala and borrowed/appropriated by European scholars (Raju 2007 pages 321-373).
The calculus first developed in India as a sophisticated technique to calculate precise trigonometric values needed for astronomical models. These values were precise to the 9th place after the decimal point; this precision was needed for the calendar, critical to monsoon-driven Indian agriculture […]. This calculation involved infinite series which were summed using a sophisticated philosophy of ratios of inexpressed numbers [today called rational functions…].
Europeans, however, were primitive and backward in arithmetical calculations […] and barely able to do finite sums. The decimal system had been introduced in Europe by Simon Stevin only at the end of the 16th c., while it was in use in India since Vedic times, thousands of years earlier.
C. K. Raju (2013 p. 161- 162)
This may be cited in contrast with the statements of western historians, among which:
The history of mathematics cannot with certainty be traced back to any school or period before that of the Greeks […] though all early races knew something of numeration […] and though the majority were also acquainted with the elements of land-surveying, yet the rules which they possessed […] were neither deduced from nor did they form part of any science.
W. W. Rouse Ball, A Short Account of the History of Mathematics. Dover, New York, 1960, p. 1–2.
So, it may seem paradoxical, given such an intellectual baggage, to write an entire chapter on musical scales without a single number! In A Mathematical Discussion of the Ancient Theory of Scales according to Natyashastra I showed a minimal reason: Bharata’s description leads to an infinite set of solutions that should be formalised with algebra rather than a set of numbers.
The experiment
The author(s) of Natya Shastra invite(s) the reader to take two vina-s (plucked stringed instruments) and tune them on the same scale.
A word of caution to clarify the context: this chapter of Natya Shastra can be read as a thought experiment rather than a process involving physical objects. There is no certainty that these two vina-s ever existed — and even that “Bharata Muni”, the author/experimenter, was a unique person. His/their approach is one of validation (pramāņa) by empirical evidence, in other words driven by the physically manifest (pratyakşa) rather than inferred from “axioms” constitutive of a theoretical model. This can be summed up as a “preference for physics over metaphysics”.
Constructing and manipulating vina-s in the manner indicated by the experimenter appears to be an insurmountable technological challenge. This has been discussed by a number of authors — see Iyengar (2017 pages 7-sq.) Leaving aside the possibility of practical realisation is not a denial of physical reality, as formal mathematics would systematically dictate. Calling it a “thought experiment” is a way of asserting the connection with the physical model. Similarly, the use of circular graphs to represent tuning schemes and algebra to describe relationships between intervals are aids to understanding that do not reduce the model to specific, idealistic interpretations similar to the speculations about integers cherished by Western scientists. These graphs are intended to facilitate the computational design of instruments that model these imagined instruments — see Raga intonation and Just intonation, a general framework.
Let us follow Bharata’s instructions and tune both instruments to a scale called “Sa-grama” about which the author explains:
The seven notes [svaras] are: Şaḍja [Sa], Ṛşbha [Ri], Gāndhāra [Ga], Madhyama [Ma], Pañcama [Pa], Dhaivata [Dha], and Nişāda [Ni].
It is tempting to identify this scale as the conventional western seven-degree scale do, re, mi, fa, sol, la, si (“C”, “D”, “E”, “F”, “A”, “B”), which some scholars have done despite the erroneous interpretation of the intervals.
Intervals are notated in shruti-s, which can be thought of as an ordering device rather than a unit of measurement. Experiment will confirm that a four-shruti interval is greater than a three-shruti, a three-shruti greater than a two-shruti and the latter greater than a single shruti. In different contexts, the word “shruti” refers to note positions rather than intervals between notes. This ambiguity is also a source of confusion.
The author writes:
Śrutis in the Şaḍja Grāma are shown as follows: three [in Ri], two [in Ga], four [in Ma], four [in Pa], three [in Dha], two [in Ni], and four [in Sa].
Bharata uses 9-shruti (consonant) intervals: “Sa-Pa”, “Sa-Ma”, “Ma-Ni”, “Ni-Ga” and “Re-Dha”. He also defines another scale called “Ma-grama” in which “Pa” is one shruti lower than “Pa” in the Sa-grama, so that “Sa-Pa” is no longer consonant whereas “Re-Pa” is consonant because it is made up of 9 shruti-s.
Intervals of 9 or 13 shruti-s are declared “consonant” (samvadi). Ignoring the octave, the best consonance in a musical scale is the perfect fifth with a frequency ratio close to 3/2. When tuning stringed instruments, a ratio other than 3/2 will produce beats indicating that a string is out of tune.
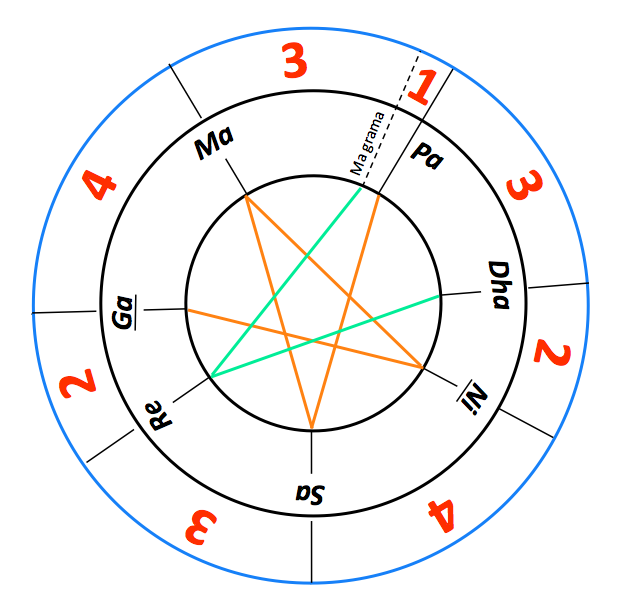
If the frequency ratios are expressed logarithmically with 1200 cents representing an octave, and further converted to angles with a full octave on a circle, the description of the Sa-grama and Ma-grama scales can be summarised on a circular diagram (see figure).
Two cycles of fifths are highlighted in red and green colors. Note that both the “Sa-Ma” and “Ma-Ni” intervals are perfect fifths, which discards the association of Sa-grama with the conventional western scale: the “Ni” should be mapped to “B flat”, not to “B”. Furthermore, the perfect fifth “Ni-Ga” implies that “Ga” is also “E flat” rather than “E”. The Sa-grama and Ma-grama scales are therefore “D modes”. This is why “Ga” and “Ni” are underlined in the diagrams.
Authors eager to identify Sa-grama and Ma-grama as a western scale have claimed that when the text says that there are “3 shruti-s in Re” it should be understood as between Re and Ga. However, this interpretation is inconsistent with the second lowering of the movable vina (see below).
We must avoid jumping to conclusions about the intervals in these scales. The two cycles of fifths are unrelated, except that the “distance” between the “Pa” of Ma-grama and that of Sa-grama is “one shruti”:
The difference which occurs in Pañcama when it is raised or lowered by a Śruti and when consequential slackness or tenseness [of strings] occurs, will indicate a typical (pramāņa) Śruti. (XXVIII, 24)
In other words, the size of this pramāņa ṣruti is not specified. It would therefore be misleading to postulate its equivalence to the syntonic comma (frequency ratio 81/80). To do so reduces Bharata’s model to “just intonation”, indeed with interesting properties in its application to western harmony (see page), but with a questionable relevance to the practice of Indian music. As stated by Arnold (1983 p. 39):
The real phenomenon of intonation in Hindustani Classical Music as practised is much more amorphous and untidy than any geometry of course, as recent empirical studies by Levy (1982), and Arnold and Bel (1983) show.
The designation of the smallest interval as “pramāņa ṣruti” is of great epistemic importance and deserves a brief explanation. The semantics of “slackness or tension” clearly belong to “pratyakṣa pramāṇa”, the means of acquiring knowledge through perceptual experience. More precisely, “pramāṇa” (प्रमाण) refers to “valid perception, measure and structure” (Wisdom Library), a notion of evidence shared by all traditional Indian schools of philosophy (Raju 2007 page 63). We will return to this notion in the conclusion.
An equivalent way of connecting the two cycles of fifths would be to define a 7-shruti interval, for example “Ni-Re”. If the pramāņa ṣruti were a syntonic comma then this interval would be a harmonic major third with a ratioof 5/4. As mentioned in Just intonation, a general framework, the invention of the major third as a consonant interval dates back to the early 16th century in Europe. In Natya Shastra this 7-shruti interval was classified as “assonant” (anuvadi).
In all writings referring to the ancient Indian theory of scales, I have occasionally used “pramāņa ṣruti” and “syntonic comma” as equivalent terms. This is acceptable if one accepts that the syntonic comma can take values other than 81/80. Consequently, the “harmonic major third” should not automatically be assigned a frequency ratio of 5/4.
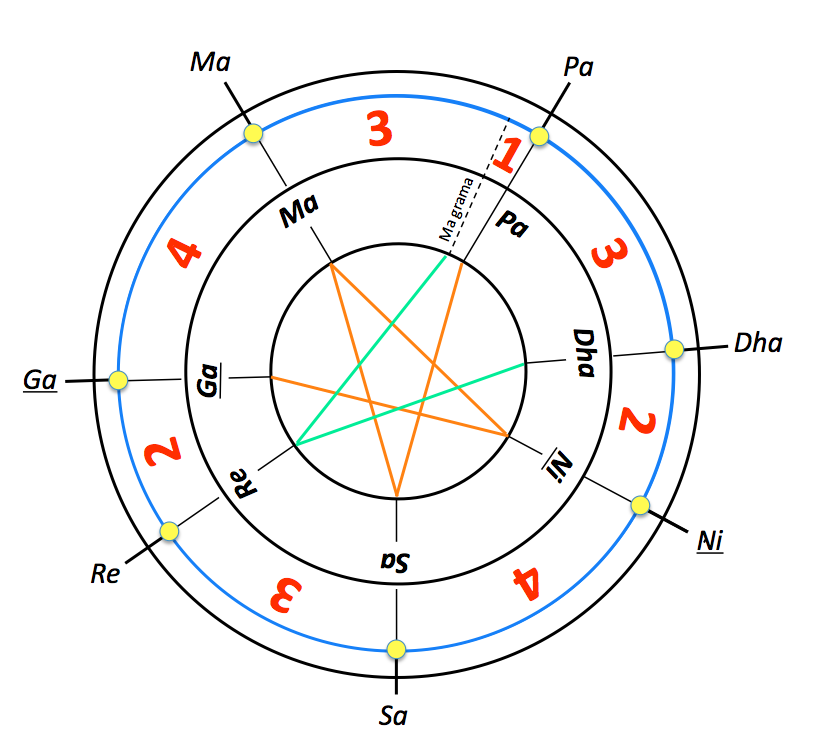
The picture above shows the two vina-s tuned identically on Sa-grama. Matching notes are marked with yellow dots. The inner part of the blue circle will be the moving vina in the following transpositions, and the outer part the fixed vina.
First lowering
Bharata writes:
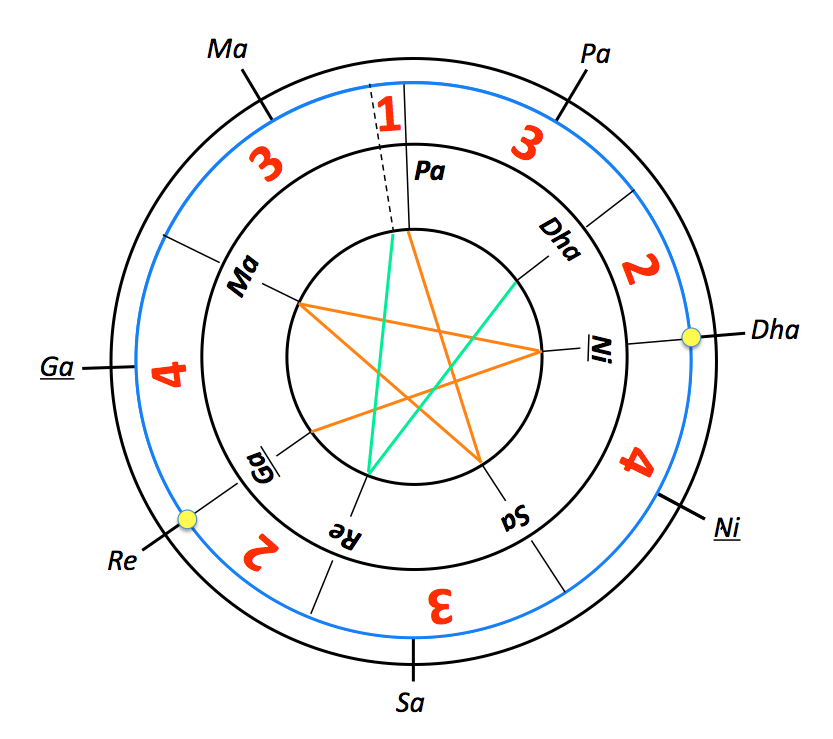
The two Vīņās with beams (danḍa) and strings of similar measure, and with similar adjustment of the latter in the Şaḍja Grāma should be made [ready]. [Then] one of these should be tuned in the Madhyama Grāma by lowering Pañcama [by one Śruti]. The same (Vīņā) by adding one Śruti (lit. due to the adding of one Śruti) to Pañcama will be tuned in the Şaḍja Grāma.
In short, this is a procedure for lowering all the notes of the movable vina by one pramāņa ṣruti. First lower its “Pa” — e.g. make it consonant with the “Re” of the fixed vina — to obtain Ma-grama on the movable vina. Then readjust its entire scale to obtain Sa-grama. Note that lowering “Re” and “Dha” means revaluing the size of a pramāņa ṣruti while maintaining the ‘Re-Dha’ consonant interval. The result is as follows:
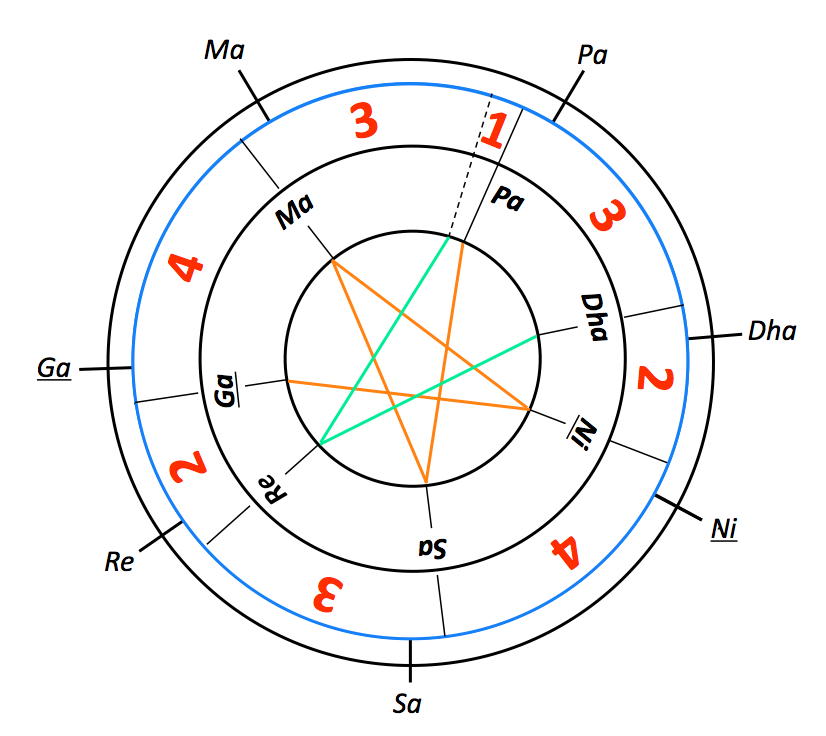
The picture illustrates the fact that there is no longer a match between the two vina-s.
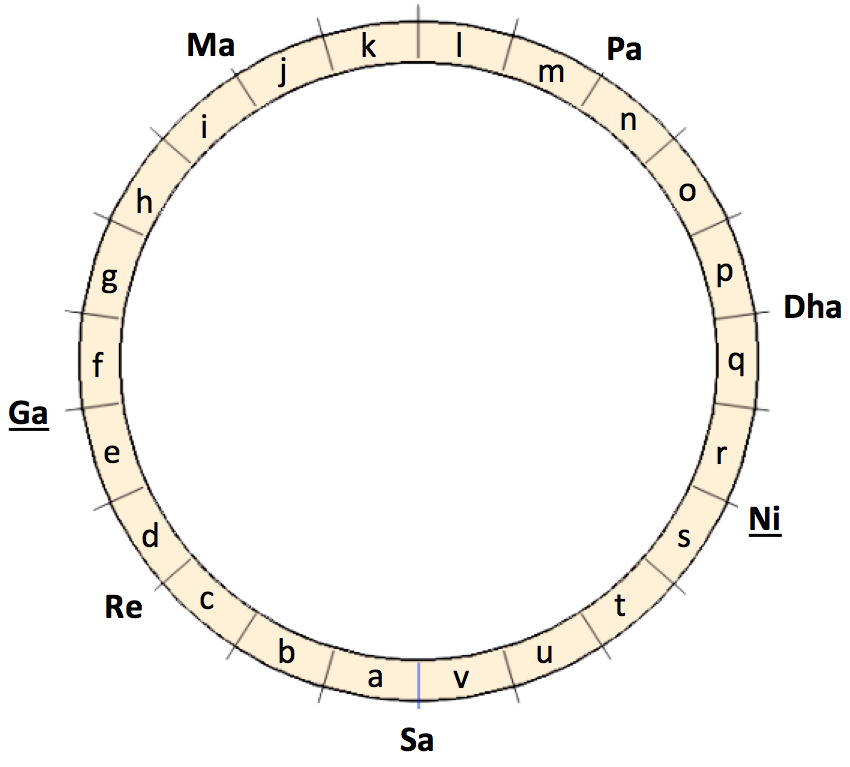
This situation can be translated into algebra. Let “a”, “b”, “c” … “v” be the unknown sizes of the shruti-s in the scale (see picture on the side). A metric that “translates” Bharata’s model will be necessary to test it on sound structures produced by an electronic instrument — the computer. The scope of this translation remains valid as long as no additional assertion is made that is not rooted in the original model.
Using the symbol “#>” to indicate that two notes do not match, this first lowering can be summarised by the following set of inequalities:
| s + t + u + v > m a + b + c > m d + e > m f + g + h + i > m n + o + p > m q + r > m | Sa #> Ni Re #> Sa Ga #> Re Ma #> Ga Dha #> Pa Ni #> Dha |
Second lowering
The next step is another lowering by one shruti using a different procedure.
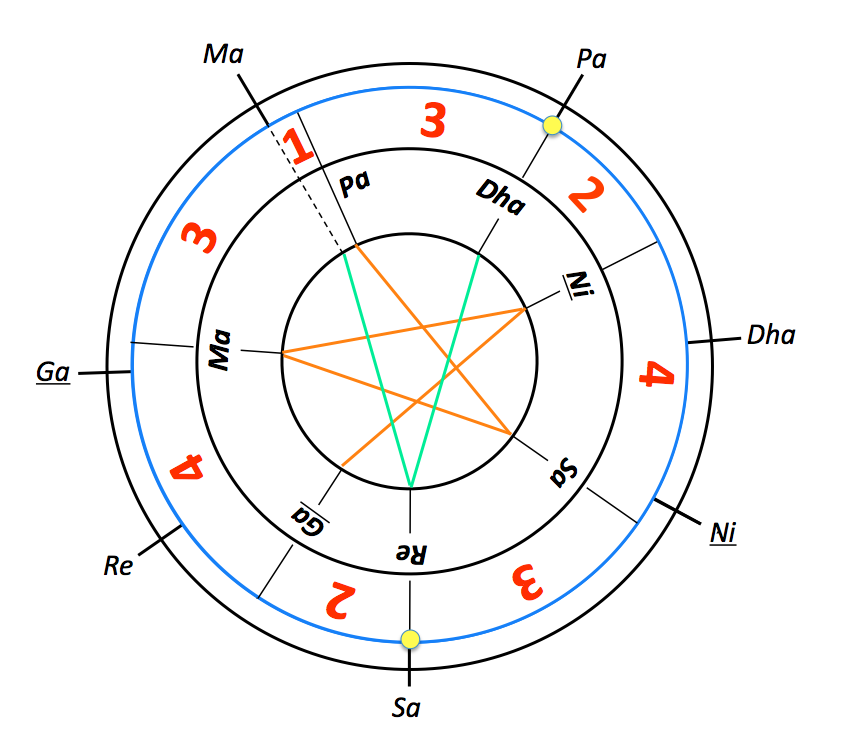
Again due to the decrease of a Śruti in another [Vīņā], Gāndhāra and Nişāda will merge with Dhaivata and Ṛşbha respectively, when there is an interval of two Śrutis between them.
Note that it is no longer possible to rely on a lowered “Pa” to evaluate a pramāņa ṣruti for the lowering. The instruction is to lower the tuning of the movable vina until either “Re” and “Ga” or “Dha” and “Ni” merge, which is claimed to be the same because of the final lowering of two shruti-s (from the initial state):
Now we have an equation which tells us that the two-shruti intervals are equal in size:
q + r = d + e
and five more inequations indicating the non-matching of other notes:
| f + g + h + i > d + e a + b + c > d + e s + t + u + v > d + e n + o + p > d + e j + k + l + m > d + e | Ma #> Ga Re #> Sa Sa #> Ni Dha #> Pa Pa #> Ma |
We should bear in mind that the author is describing a physical process, not an abstract “movement” by which the moving wheel (or vina) would “jump” in space from its initial to final position. Therefore, we pay attention to what happens and what does not happen during the tuning of the vina or the rotation of the wheel by looking at the trajectories of the dots representing the note positions (along the blue circle). Things that do not happen (mismatched notes) give rise to inequations that are necessary to make sense of the algebraic model.
This step of the experiment confirms that it is wrong to place Sa in the position of Ni in order to identify Sa-grama with the Western scale. In this case the corresponding notes would not be Re-Ga and Dha-Ni, but Ga-Ma and Ni-Sa.
Third lowering
Bharata writes:
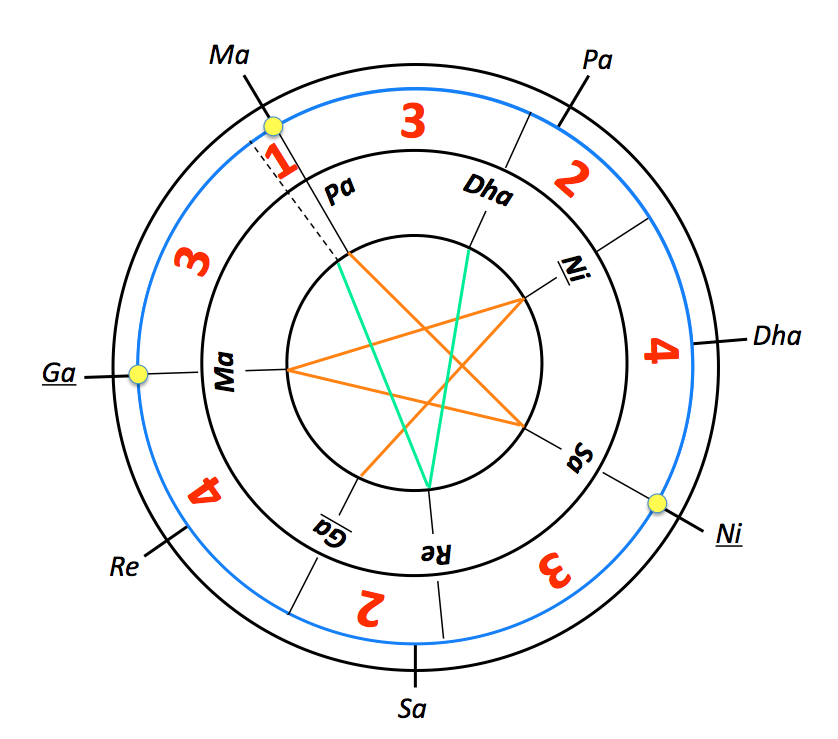
Again due to the decrease of a Śruti in another [Vīņā], Ṛşbha and Dhaivata will merge with Şaḍja and Pañcama respectively, when there is an interval of three Śrutis between them.
This leads to equation
n + o + p = a + b + c
and inequations:
| s + t + u + v > a + b + c f + g + h + i > a + b + c j + k + l + m > a + b + c | Sa #> Ni Ma #> Ga Pa #> Ma |
Fourth lowering
The procedure:
Similarly the same [one] Śruti being again decreased, Pañcama, Madhyama and Şaḍja will merge with Madhyama, Gāndhāra and Nişāda respectively when there is an interval of four Śrutis between them.
This yields 2 equations:
j + k + l + m = f + g + h + i
s + t + u + v = f + g + h + i
Algebraic interpretation
After eliminating redundant equations and inequations, the constraints are summarised as follows:
(S1) d + e > m
(S2) a + b + c > d + e
(S3) f + g + h + i > a + b + c
(S4) j + k + l + m = f + g + h + i
(S5) s + t + u + v = f + g + h + i
(S6) n + o + p = a + b + c
(S7) q + r = d + e
The three inequations illustrate the fact that the numbers of shruti-s denote an ordering of the sizes of the intervals between notes.
We still have 22 variables and only 4 equations. These variables can be “packed” into a set of 8 variables representing the “macro-intervals”, i.e. the steps of the grama-s. In this approach the shruti-s are a kind of “subatomic” particles of which these “macro-intervals” are made… Now we need only 4 auxiliary equations to determine the scale. These can be provided by acoustic information where the intervals are counted in cents. First we express that the sum of the variables, the octave, is equal to 1200 cents. (A larger value, e.g. 1204, could be used to devise extended octaves).
(S8) (a + b + c) + (d + e) + (f + g + h + i) + (j + k + l) + m + (n + o + p) + (q + r) + (s + t + u + v) = 1200
Then we interpret all samvadi ratios as perfect fifths (ratio 3/2 = 701.9 cents):
(S9) (a + b + c) + (d + e) + (f + g + h + i) + (j + k + l) + m = 701.9 (Sa-Pa)
(S10) (j + k + l) + m + (n + o + p) + (q + r) + (s + t + u + v) = 701.9 (Ma-Sa)
(S11) (d + e) + (f + g + h + i) + (j + k + l) + m + (n + o + p) = 701.9 (Re-Dha)
(S12) (f + g + h + i) + (j + k + l) + m + (n + o + p) + (q + r) = 701.9 (Ga-Ni)
including the “Re-Pa” perfect fifth in Ma-grama:
(S13) m + (n + o + p) + (q + r) + (s + t + u + v) + (a + b + c) = 701.9
S10, S11 and S12 can all be derived from S9. So these equations can be discarded. We still need one more equation to solve the system. At this stage there are many options in terms of tuning procedures. As suggested above, setting the harmonic major third to the ratio 5/4 (386.3 cents) would provide the missing equation. This is equivalent to setting the variable “m” to 21.4 cents (syntonic comma). However, this major third can be any size up to the Pythagorean third (81/64 = 407.8 cents), for which we would get m = 0.
Beyond this range, the two-vina experiment is no longer valid, but it leaves a large number of possibilities, including the temperament of some intervals, which musicians might spontaneously achieve in parallel melodic movements. A number of solutions are presented in A Mathematical Discussion of the Ancient Theory of Scales according to Natyashastra, and some of these have been tried on the Bol Processor to check musical examples for which they might provide adequate scales — see Raga intonation.
Extensions of the model
To complete his system of scales, Bharata needed to add two new notes to the basic grama-s: antara Gandhara and kakali Nishada. The new “Ga” is defined as “G” raised by 2 shruti-s. Similarly, kakali Ni is “N” raised by 2 shruti-s.
In order to position “Ni” and “Ga” correctly we must study the behaviour of the new scale in all transpositions (murcchana-s), including those beginning with “Ga” and “Ni”, and derive equations corresponding to an optimal consonance of the scale. We end up with 11 equations for only 10 variables, which means that this perfection cannot be achieved. One constraint must be released.
One option is to release the constraints on major thirds, fifths or octaves, resulting in a form of temperament. For example, stretching the octave by 3.7 cents produces perfect fifths (701.9 cents) and harmonic major thirds close to equal temperament (401 cents) with a comma of 0 cents. This tuning technique was advocated by Serge Cordier (Asselin 2000 p. 23; Wikipedia).
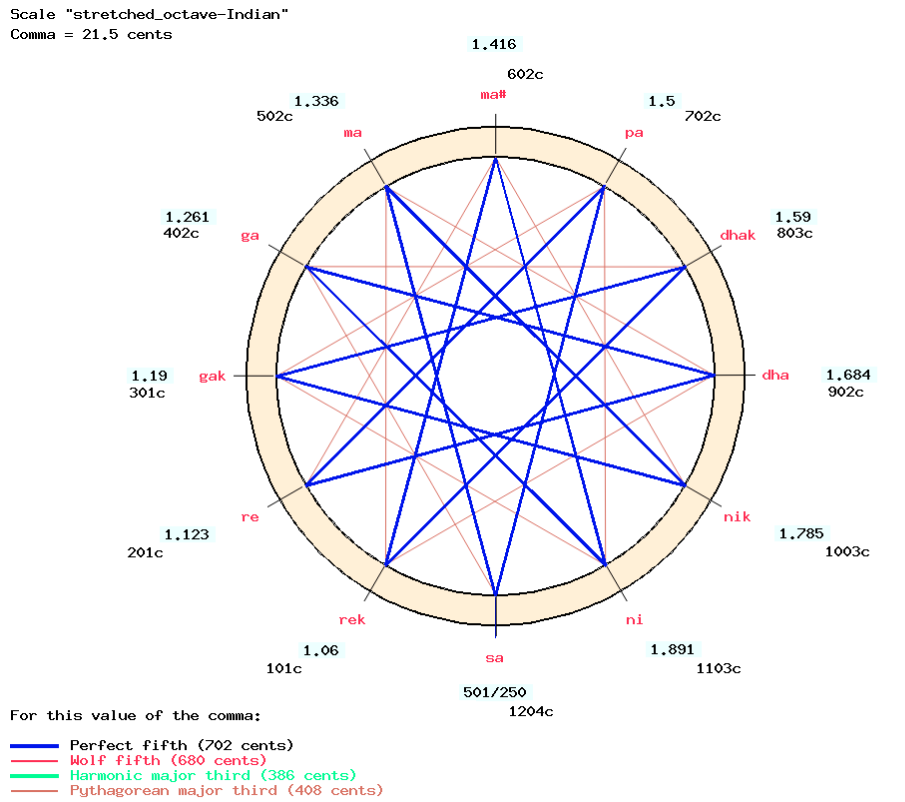
Another option is to get as close as possible to “just intonation” without changing perfect fifths and octaves. This is possible by allowing the comma (variable “m”) to take any value between 0 and 56.8 cents. Limits are imposed by the inequations derived from the two-vina experiment.
These “just systems” are calculated as follows:
a + b + c = j + k + l = n + o + p = Maj - C
d + e = h + i = q + r = u + v = L + C
f + g = s + t = Maj - L - C
m = C
where L = 90.25 cents (limma = 256/243), Maj = 203.9 cents (major wholetone = 9/8)
and 0 < C < 56.8 (pramāņa ṣruti or syntonic comma)
This leads to the 53-degree scale called “grama” which we use as a framework for consonant chromatic scales suitable for pure intonation in western harmony when the syntonic comma is sized 81/80. Read Just intonation, a general framework:
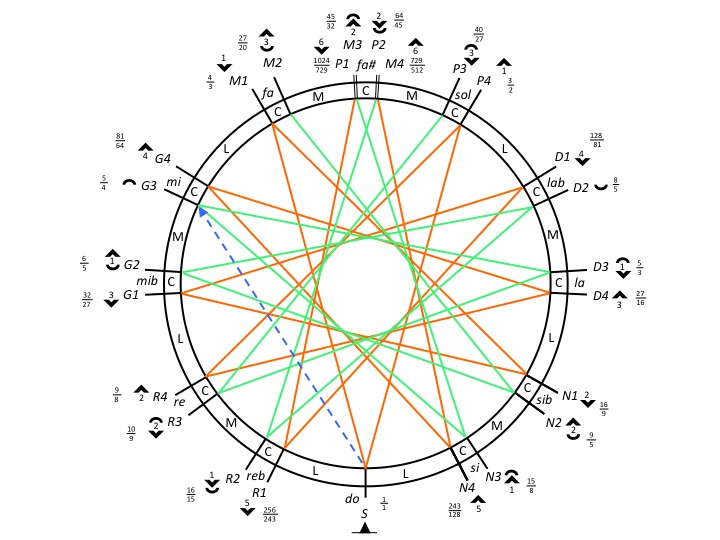
In BP3, the just-intonation framework has been extended so that any value of the syntonic comma (or the harmonic major third) can be set on a given scale structure. This feature is demonstrated on the Raga intonation page.
The relevance of circular representations
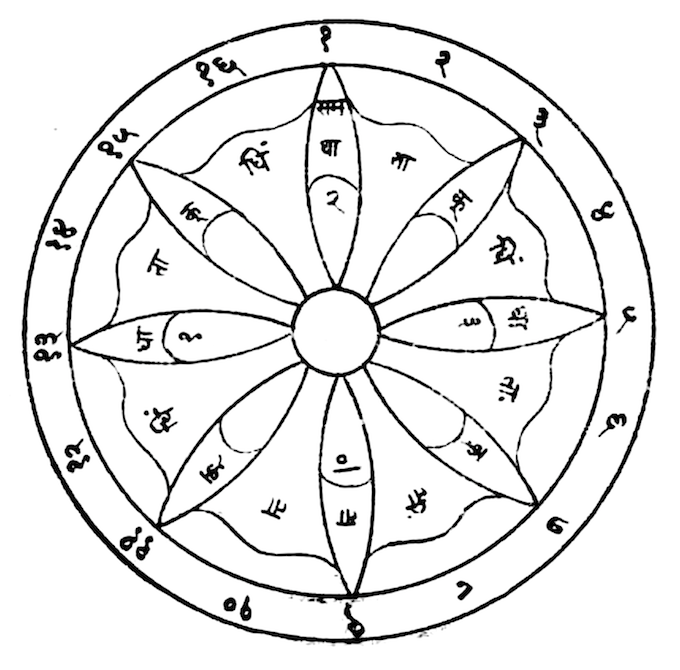
Circular representation of tāl Pañjābi, catuśrajāti
[16 counts] from a Gujarati text in Devanagari script
(J. Kippen, pers. communication)
It is safe to classify the two-vina experiment as a thought experiment, since it is unlikely that it could be carried out with mechanical instruments. Representing it on a circular graph (a movable wheel inside a fixed crown) achieves the same goal without resorting to imaginary devices.
Circular representations belong to Indian traditions of various schools, including the description of rhythmic cycles (tāl-s) used by drummers. These diagrams are meant to outline the rich internal structure of musical constructions that cannot be reduced to “beat counting” (Kippen 2020).
For example, the image on the side was used to describe the ţhekkā (cycle of quasi-onomatopoeic syllables representing the beats of the drum) of tāl Pañjābi which reads as follows:

Unfortunately, early printing technology may have made the publication and transmission of these learning aids difficult.
If Bharata’s contemporaries ever used similar circular representations to reflect on musical scales, we suspect that archaeological traces might not be properly identified, as their drawings might be mistaken for yantra-s, astrological charts and the like!
Return to epistemology
Bharata’s experiment is a typical example of the preference for facts derived from empirical observation over a proclaimed universal logic aimed at establishing “irrefutable proofs”.
Empirical proofs are universal, not metaphysical proofs; eliminating empirical proofs is contrary to all systems of Indian philosophy. Thus elevating metaphysical proofs above empirical proofs, as formal mathematics does, is a demand to reject all Indian philosophy as inferior. Curiously, like Indian philosophy, present-day science too uses empirical means of proof, so this is also a demand to reject science as inferior (to Christian metaphysics).
Logic is not universal either as Western philosophers have foolishly maintained: Buddhist [quasi truth-functional] and Jain [three-valued] logics are different from those currently used in formal mathematical proof. The theorems of mathematics would change if those logics were used. So, imposing a particular logic is a means of cultural hegemony. If logic is decided empirically, that would, of course, kill the philosophy of metaphysical proof. Further, it may result in quantum logic, similar to Buddhist logic […].
C. K. Raju (2013 p. 182-183)
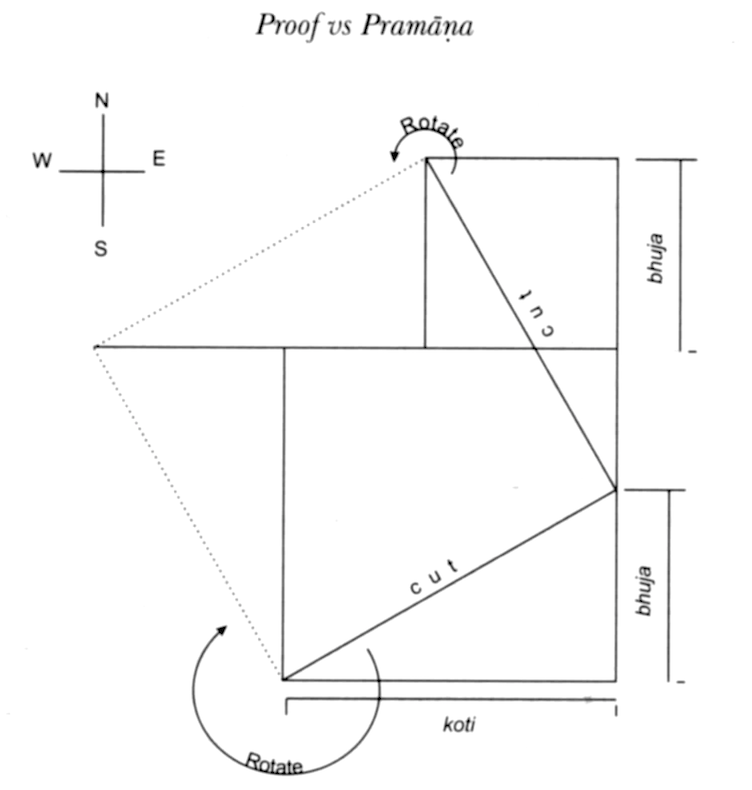
Source: C. K. Raju (2007 p. 67)
The two-vina experiment can be compared to the (more recent) physical proof of the “Pythagorean theorem”. This theorem (Casey 1885 p. 43) was known in India and Mesopotamia long before the time of its legendary author (Buckert 1972 p. 429, 462). In the Indian text Yuktibhāşā (c. 1530 CE), a figure of a right-angled triangle with squares on either side and its hypothenuse is drawn on a palm leaf. The figure is then cut and rotated to show that the areas are equal.
Obviously, the proof of the “Pythagorean Theorem” is very easy if you are either (a) allowed to take measurements or, equivalently, (b) allowed to move figures around in space.
C. K. Raju (2013 p. 167)
This process takes place in several stages of moving figures, similar to the moving scales (or figures representing scales) in the two-vina experiment. The 3 single-shruti tone intervals can be compared to the areas of the 3 squares in Yuktibhāşā. The following comment would therefore apply to Bharata’s procedure:
The details of this rationale are not our immediate concern beyond observing that drawing a figure, carrying out measurements, cutting, and rotation are all empirical procedures. Hence, such a demonstration would today be rejected as invalid solely on the ground that it involves empirical procedures that ought not to be any part of mathematical proof.
C. K. Raju (2007 p. 67)
Bernard Bel — Dec. 2020
References
Arnold, E. J. A Mathematical model of the Shruti-Swara-Grama-Murcchana-Jati System. New Delhi, 1982: Journal of the Sangit Natak Akademi.
Arnold, E.J.; Bel, B. A Scientific Study of North Indian Music. Bombay, 1983: NCPA Quarterly Journal, vol. XII Nos. 2 & 3.
Asselin, P.-Y. Musique et tempérament. Paris, 1985, republished in 2000: Jobert. Soon available in English.
Bel, B.; Bor, J. Intonation of North Indian Classical Music: working with the MMA. Video on Dailymotion. Bombay, 1984: National Center for the Performing Arts.
Bel, B.; Bor, J. NCPA/ISTAR Research Collaboration. Bombay, 1985: NCPA Quarterly Journal, vol. XIV, No. 1, p. 45-53.
Bel, B. A Mathematical Discussion of the Ancient Theory of Scales according to Natyashastra. Note interne. Marseille, 1988a : Groupe Représentation et Traitement des Connaissances (CNRS).
Bel, B. Raga : approches conceptuelles et expérimentales. Actes du colloque “Structures Musicales et Assistance Informatique”. Marseille, 1988b.
Bharata. Natya Shastra. There is no currently available English translation of the first six chapters of Bharata’s Natya Shastra. However, most of the information required for this interpretation has been reproduced and commented by Śārṅgadeva in his Sangita Ratnakara (13th century CE), translated by Dr R. K. Shringy, vol.I. Banaras 1978: Motilal Banarsidass.
Bose, N. D. Melodic Types of Hindustan. Bombay, 1960: Jaico.
Burkert, W. Lore and Science in Ancient Pythagoreanism. Cambridge MA, 1972: Harvard University Press.
Casey, J. The First Six Books of the Elements of Euclid, and Propositions I.-XXI. of Book VI. London, 1885: Longmans. Free e-book, Project Gutenberg.
Iyengar, R. N. Concept of Probability in Sanskrit Texts on Classical Music. Bangalore, 2017. Invited Talk at ICPR Seminar on “Science & Technology in the Indic Tradition: Critical Perspectives and Current Relevance”, I. I. Sc.
Kippen, J. Rhythmic Thought and Practice in the Indian Subcontinent. In R. Hartenberger & R. McClelland (Eds.), The Cambridge Companion to Rhythm (Cambridge Companions to Music, p. 241-260). Cambridge, 2020: Cambridge University Press. doi:10.1017/9781108631730.020
Levy, M. Intonation in North Indian Music. New Delhi, 1982: Biblia Impex.
Raju, C. K. Cultural foundations of mathematics : the nature of mathematical proof and the transmission of the calculus from India to Europe in the 16th c. CE. Delhi, 2007: Pearson Longman: Project of History of Indian Science, Philosophy and Culture : Centre for Studies in Civilizations.
Raju, C. K. Euclid and Jesus: How and why the church changed mathematics and Christianity across two religious wars. Penang (Malaysia), 2013: Multiversity, Citizens International.
Rao, S.; Van der Meer, W. The Construction, Reconstruction, and Deconstruction of Shruti. Hindustani music: thirteenth to twentieth centuries (J. Bor), Manohar, New Delhi 2010.
Shringy, R.K.; Sharma, P.L. Sangita Ratnakara of Sarngadeva: text and translation, vol. 1, 5: 7-9. Banaras, 1978: Motilal Banarsidass. Source in the Web Archive.