Just intonation (intonation pure in French) is a word used by composers, musicians and musicologists to describe various aspects of composition, performance and instrument tuning. They all point to the same goal of "playing/singing in tune" — whatever that means. Implementing a generic abstract model of just intonation in the Bol Processor is a challenge beyond our current competence… We approach it pragmatically by looking at some musical traditions that pursue the same goal with the help of reliable theoretical models.
A complete and consistent framework for the construction of just-intonation scales - or "tuning systems" - was the grama-murcchana model elaborated in ancient India. This theory has been extensively commented on and (mis)interpreted by Indian and Western scholars: for a detailed review see Rao & van der Meer 2010. We will show that an arguably acceptable interpretation yields a framework of chromatic scales that can be extended to Western classical harmony and easily handled by the Bol Processor + Csound.
This page is a continuation of Microtonality but can be read independently.
All examples shown on this page are available in the sample set bp3-ctests-main.zip shared on GitHub. Follow instructions on Bol Processor ‘BP3’ and its PHP interface to install BP3 and learn its basic operation. Download and install Csound from its distribution page.
Historical background
Methods of tuning musical instruments have been documented in various parts of the world for over 2000 years. For practical and personal reasons we will concentrate on work in Europe and the Indian subcontinent.
Systems described as "just intonation" are attempts to create a tuning in which all tonal intervals are consonant. There is a large body of theoretical work on just intonation - see Wikipedia for links and abstracts.
Models are amenable to Hermann von Helmholtz's notion of consonance which deals with the perception of the pure sinusoidal components of complex sounds containing multiple tones. According to the theory of consonance, the frequencies of these upper partials are integer multiples of the fundamental frequency of the vibration. In mechanical musical instruments, this is close to reality when long strings are gently struck or plucked. However, this harmony is lacking in many wind instruments, especially reed instruments such as the saxophone or the Indian shehnai, and even in percussion instruments or bells which combine several modes of vibration.
Therefore, if just intonation is invoked to. tune a musical instrument, it must be analogous to a zither, a swara mandal, a harpsichord, a piano or a pipe organ, including electronic devices that produce similar sounds.
Perhaps because of their late "discovery" of calculus — actually "borrowed" from Indian, Persian and Arabic sources — Europeans cultivated a fascination with numbers strongly advocated by priests as an image of "God's perfection". We may recall Descarte's claim that the length of a curve is "beyond human understanding" — because π cannot be written as an integer ratio…
In real life, musicians developed procedures for tuning their instruments by listening to intervals and picking out the ones that made sense to their ears — see The two-vina experiment page. After the development of musical acoustics, attempts were made to interpret these procedures in terms of frequency ratios. This was a risky venture, however, because the dream of perfection led to the simplistic promotion of "perfect ratios".
Seeking the kind of perfection embodied in numbers is the best way to produce bland music. Although just intonation — intervals without beats — is now possible on electronic instruments, it is based on a narrow concept of tonality. This can be verified by listening to ancient Western music played in different temperaments — see page Comparing temperaments — and even to Indian classical music — see page Raga intonation.
The "Greek" approach

Models of vibrating strings attributed to the "ancient Greeks" suggest that frequency ratios of 2/1 (the octave), 3/2 (the major fifth) and 5/4 (the major third) produce consonant intervals, while other ratios produce a certain degree of dissonance.
The practice of polyphonic music on fixed-tuned instruments has shown that this perfect consonance is never achieved with 12 notes in an octave — the conventional chromatic scale. In Western classical harmony, it would require retuning the instrument according to the musical genre, the piece of music and the harmonic context of each melodic phrase or chord.
Imperfect tonal intervals produce unwanted beats because their frequency ratio cannot be reduced to simple 2, 3, 4, 5 fractions. A simple thought experiment, mythically attributed to Pythagoras of Samos, shows that this is inherent in arithmetic and not a defect in instrument design. Imagine the tuning of ascending fifths (ratio 3/2) by successive steps on a harp with an octave shift to keep the resulting note within the original octave. The frequency ratios would be 3/2, 9/4, 27/16, 81/64 and so on. At this stage, the note appears to be a major third although its actual ratio (81/64 = 1.265) is higher than 5/4 (1.25). The 81/64 interval is called the Pythagorean major third, which may sound "out of tune" in a conventional harmonic context. The frequency ratio (81/80 = 1.0125) between the Pythagorean and harmonic major thirds is called the syntonic comma.
Whoever devised the so-called "Pythagorean tuning" went further in their intention to describe all musical notes by cycles of fifths. Going further up, 243/128, 729/512… etc. effectively produces a full chromatic scale: C - G - D - A - E - B - F♯ - C♯ - G♯… etc. But in addition to the harsh sound of some of the resulting intervals, things get bad if one hopes to end the cycle on the initial note. If the series started on 'C', it will end on 'C' (or 'B#'), but with a ratio of 531441/524288 = 1.01364, slightly higher than 1. This gap is called the Pythagorean comma, which is conceptually different from the syntonic comma (1.0125), although their sizes are almost identical. This paradox is a matter of simple arithmetic: powers of 2 (octave intervals) never equal powers of 3.
The attribution of this system to the "ancient Greeks" is, of course, pure fantasy, since they (unlike the Egyptians) didn't have any use for fractions!
Despite the comma problem, tuning instruments by series of perfect fifths was common practice in medieval Europe, following the organum which consisted of singing/playing parallel fifths or fourths to enhance a melody. One of the oldest treatises on "Pythagorean tuning" was published around 1450 by Henri Arnault de Zwolle (Asselin 2000 p. 139). In this tuning, major "Pythagorean" thirds sounded harsh, which explains why the major third was considered a dissonant interval at the time.
Because of these limitations, Western fixed-pitch instruments using chromatic (12-tone) scales never achieve the pitch accuracy dictated by just intonation. For this reason just intonation is described in the literature as "incomplete" (Asselin 2000 p. 66). Multiple divisions (more than 12 per octave) are required to produce all "pure" ratios. This has been unsuccessfully attempted on keyboard instruments, although it remains possible on a computer.
The Indian approach

The grama-murcchana model was described in the Natya Shastra, a Sanskrit treatise on the performing arts written in India some twenty centuries ago. Chapter 28 contains a discussion of the "harmonic scale", which is based on a division of the octave into 22 shruti-s, while only seven swara-s (notes) are used by musicians: "Sa", "Re", "Ga", "Ma", "Pa", "Dha", "Ni". These can be mapped onto conventional Western music notation "C", "D", "E", "F", "G", "A", "B" in English, or "do", "re", "mi", "fa", "sol", "la", "si" in Italian/Spanish/French.
This 7-swara scale can be extended to a 12-degree (chromatic) scale by means of diesis and flat alterations, which raise or lower a note by a semitone. Altered notes in the Indian system are commonly called "komal Re", "komal Ga", "Ma tivra", "komal Dha" and "komal Ni". The word "komal" can be translated as "flat" and "tivra" as "diesis".
The focus of 20th century research in Indian musicology has been to 'quantify' shruti-s in a systematic way and to assess the relevance of this quantification to the performance of classical raga.
A striking point in the ancient Indian theory of musical scales is that it does not rely on numerical ratios, be they frequencies or lengths of vibrating strings. This point was overlooked by 'colonial musicologists' because of their lack of insight into Indian mathematics and their fascination with a mysticism of numbers inherited from Neopythagoreanism.
As reported by Jonathan Barlow (personal communication, 3/9/2013, links my own):
The ustads in India from way back considered that they followed Pythagoras, but early on they made the discovery that trying to tune by numbers was a losing game, and Ibn Sina (Avicenna) (980-1037 AD), who was their great philosopher of aesthetics, said in plain terms that it was wiser to rely on the ears of the experts. Ahobala tried to do the numbers thing (and Kamilkhani) but they are relegated to a footnote of 17th C musicology.
Bharata Muni, the author(s) of the Natya Shastra, may have heard of "Pythagorean tuning", a theory that Indian scientists could have expanded considerably, given their maturity in the use of calculus.. Despite this, not a single number is quoted in the entire chapter on musical scales. This paradox is discussed on my page The Two-vina experiment. In A Mathematical Discussion of the Ancient Theory of Scales according to Natyashastra, I showed a minimal reason: Bharata's description leads to an infinite set of solutions, which should be formalised with some algebra, rather than a set of integer ratios.
How (and why) should the octave be divided into 22 micro-intervals when most Indo-European musical systems only name 5 to 12 notes? Some naive ethnomusicologists have claimed that Bharata's model must be a variant of the Arabic "quartertone system", or even a tempered scale with 22 intervals… If so, why not 24 shruti-s? Or any arbitrary number? The two-vina experiment produces shruti-s of unequal sizes. No sum of microtones of 54.5 cents in a 22-degree tempered scale would produce an interval close to 702 cents — the perfect fifth that gives consonance (samvadi) to musical scales.
In the (thought?) experiment described in Natya Shastra (chapter 28), two vina-s — stringed instruments similar to zithers — are tuned identically. The author suggests lowering all the notes of one instrument by "one shruti" and he gives a list of notes that will match between the two instruments. The process is repeated three more times until all the matches have been made explicit. This gives a system of equations (and inequations) for the 22 unknown variables. Additional equations can be derived from a preliminary statement that the octave and the major fifth are "consonant" (samvadi), thus fixing ratios close to 2/1 and 3/2. (Read the detailed procedure on my page The Two-vina Experiment and the mathematics in A Mathematical Discussion of the Ancient Theory of Scales according to Natyashastra.)
However, a new equation is needed, which Bharata's model does not provide. Interestingly, in Natya Shastra the major third is classified as "assonant" (anuvadi). Setting its frequency ratio to 5/4 is therefore a reduction of this model. In fact, it is a discovery of European musicians in the early 16th century — when fixed-pitch keyboard instruments had become popular (Asselin 2000 p. 139) — that many musicologists take for granted in their interpretation of the Indian model. […] thirds were considered interesting and dynamic consonances along with their inverse, sixths, but in medieval times they were considered dissonances unusable in a stable final sonority (Wikipedia).
The reduction of Bharata's model does not fit with the flexibility of intonation schemes in Indian music — see page Raga intonation. Experimental work on musical practice is not "in tune" with this interpretation of the theory. The shruti system should be interpreted as a "flexible" framework in which the variable parameter is the syntonic comma, namely the difference between a Pythagorean major third and a harmonic major third. Adherence to the two-vina experiment only implies that the comma takes its value between 0 and 56.8 cents (Bel 1988a).

➡ Measurements in "cents" refer to a logarithmic scale. Given a frequency ratio 'r', its cent value is 1200 x log(r) / log(2). The octave (ratio 2/1) is 1200 cents, and each semitone is about 100 cents.
The construction and evaluation of raga scale types based on this flexible model is explained on my page Raga intonation.
Extending the Indian model to Western harmony
One incentive for applying the Indian framework to Western classical music is that both traditions have given priority to the consonance of perfect fifths associated with a 3/2 frequency ratio. In addition, let us agree to fix the harmonic major third to the interval 5/4 (384 cents), resulting in a syntonic comma of 81/80 (close to 21.5 cents). The system of equations derived from the two-vina experiment is complete, and it yields two additional sizes of shruti-s: the Pythagorean limma (256/243 = about 90 cents) and the minor semitone (25/24 = about 70 cents).
These intervals were known to Western musicologists who were trying to find just intonation scales that could be played on keyboard instruments (12 degrees per octave). Gioseffo Zarlino (1517-1590) is a well-known contributor to this theoretical work. His "natural scale" was an arrangement of the three natural intervals yielding the following chromatic scale — named "just intonation" in "-cs.tryScales":
(Image created by Bol Processor)
➡ This should not be confused with Zarlino's meantone temperament (image), read pages Microtonality and Comparing temperaments.
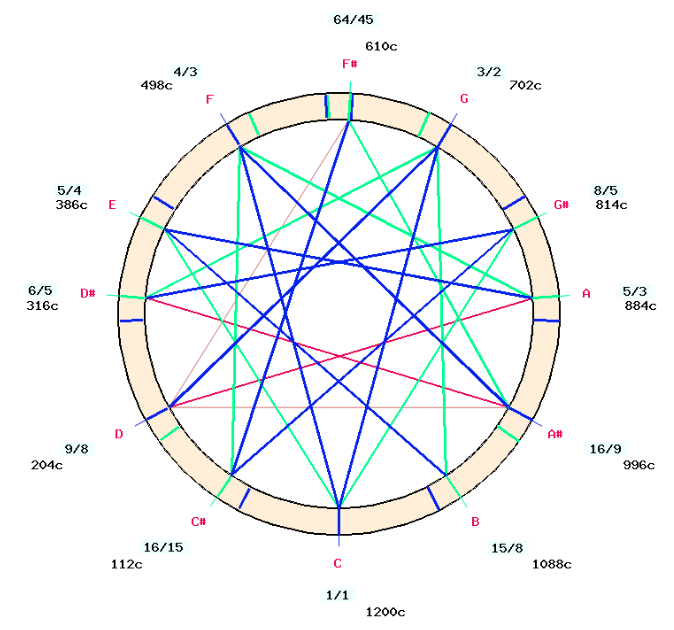
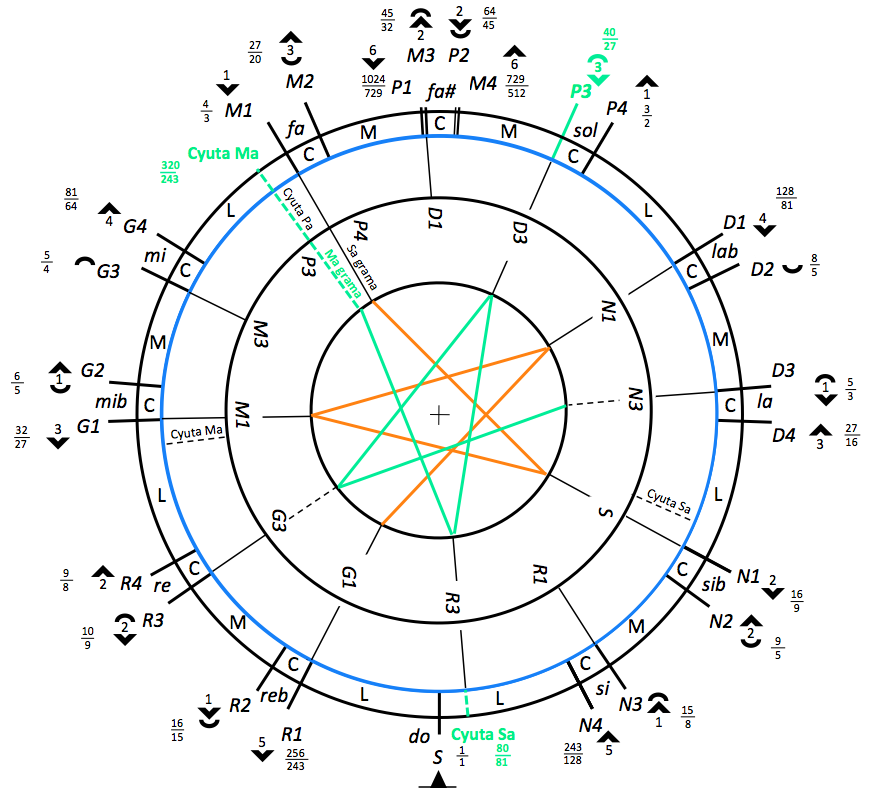
In 1974, E. James Arnold, inspired by the French musicologist Jacques Dudon, designed a circular model to illustrate the transposition of scales (murcchana) in Bharata's model. Below is the sequence of intervals (L, C, M…) over an octave as derived from the two-vina experiment.
Positions R1, R2 etc. are labelled with abbreviations of names Sa, Re, Ga, Ma, Pa, Dha, Ni. For example, Ga ("E" in English) can have four positions, G1 and G2 being enharmonic variants of komal Ga ("E flat" = "mi bemol"), while G3 and G4 are the harmonic and Pythagorean positions of shuddha Ga ("E"= "mi") respectively.
The notes of the chromatic scale have been labelled using the Italian/Spanish/French convention "do", "re", "mi", "fa"… rather than the English convention to avoid confusion: "D" is associated with Dha ("A" in English, "la" in Italian/French) and not with the English "D" ("re" in Italian/French).
Frequency ratios are illustrated by pictograms showing how each position can be derived from the base note (Sa). For example, the pictogram near N2 ("B flat" = "si bémol") shows 2 ascending perfect fifths and 1 descending major third.
Cycles of perfect fifths have been marked with red and green segments. The red series is generally called "Pythagorean" — containing G4 (81/84) — and the green one "harmonic" — containing G3 (5/4). The blue arrow shows a harmonic major third going from S ("C" = "do") to G3. Both cycles are identical, with the harmonic and Pythagorean positions differing by 1 syntonic comma.
Theoretically, the harmonic series could also be constructed in a "Pythagorean" way, by extending the cycles of perfect fifths. Thus, after 8 descending fifths, G3 ("E" = "mi") would be 8192/6561 (1.248) instead of 5/4 (1.25). The difference is a schisma (ratio 1.001129), an interval beyond human perception. It is therefore more convenient to show simple ratios.
The framework implemented in Bol Processor deals with integer ratios, which allows for high accuracy. Nevertheless, it deliberately erases schisma differences. This is the result of approximating certain ratios, e.g. replacing 2187/2048 with 16/15.
Note that there is no trace of schisma in the classical Indian theory of musical scales; there wouldn't be even if Bharata's contemporaries had constructed them via series of rational numbers, because of their decision to disregard infinitesimals as "non-representable" entities (cf. Nāgārjuna's śūniyavāda philosophy, Raju 2007 p. 400). If 2187/2048 and other complex ratios of the same series were deemed impractical, the Indian mathematician/physicist (following the Āryabhaţīya) would replace them all with "16/15 āsanna (near value)"… This is an example of Indian mathematics designed for calculation rather than proof construction. In the Western Platonic approach, mathematics aimed at "exact values" as a sign of perfection, which led its proponents to face serious problems with "irrational" numbers and even with the logic underlying formal proof procedures (Raju 2007 p. 387-389).
This diagram, and the moving grama wheel that will be introduced next, could be built with any size of the syntonic comma in the range 0 to 56.8 cents (Bel 1988a). The two-vina experiment implies that L = M + C. Thus, the syntonic comma is also the difference between a limma and a minor semitone. To build a framework for the flexible model, simply allow all harmonic positions to move by the same amount in the direction of their Pythagorean enharmonic variants.
While major thirds would be 1 comma larger if a Pythagorean interval (e.g. G4, ratio 81/64) were chosen instead of a harmonic one (G3, ratio 5/4), major fifths also differ by 1 comma, but the Pythagorean fifth (P4, ratio 3/2) is larger than the harmonic one (P3, ratio 40/27). The latter has been called the wolf fifth because its use in melodic phrases or chords is said to sound "out of tune", with a negative/evil magical connotation.
No position on this model requires more than 1 ascending or descending major third. This makes sense to instrument tuners who know that tuning perfect fifths by ear is an easy task that can be repeated in several steps — here a maximum of 5 or 6 up and down. Tuning a harmonic major third, however, requires a little more attention. It would therefore be unrealistic to imagine a precise tuning procedure based on a sequence of major thirds —although this can be achieved with the aid of electronic devices.
At the top of the picture (position "fa#") we notice that neither of the two cycles of fifths closes on itself due to the presence of a Pythagorean comma. The tiny difference (schisma, ratio 1.001129) between Pythagorean and syntonic commas is illustrated by two pairs of positions: P1/M3 and P2/M4.
Another peculiarity at the top of the picture is the apparent disruption of the sequence L-C-M. However, remembering that L = M + C, the regularity is restored by choosing between P1/M3 and P2/M4.
Approximations have no effect on the sound of musical intervals, since no human ear would appreciate a schisma difference (2 cents). However, other differences must remain explicit, since integer ratios indicate the tuning procedure by which the scale can be constructed. Thus the replacement integer ratio may be more complex than the "schismatic" one, as in the case of R1, ratio 256/243 instead of 135/128, because the latter is built with a simple major third above D4 instead of belonging to the Pythagorean series.
Tuning Western instruments
The problem of tuning fixed pitch instruments (harpsichord, pipe organ, pianoforte…) has been well documented by the organ/harpsichord player, builder and musicologist Pierre-Yves Asselin (Asselin 2000). In his practical approach, just intonation is a background model that can only be approximated on 12-degree scales by temperament — compromising the pure intervals of just intonation to meet other requirements. Temperament techniques applied to the Bol Processor are discussed on the Microtonality and Comparing temperaments pages.
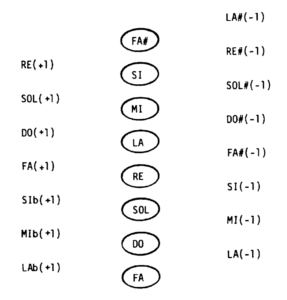
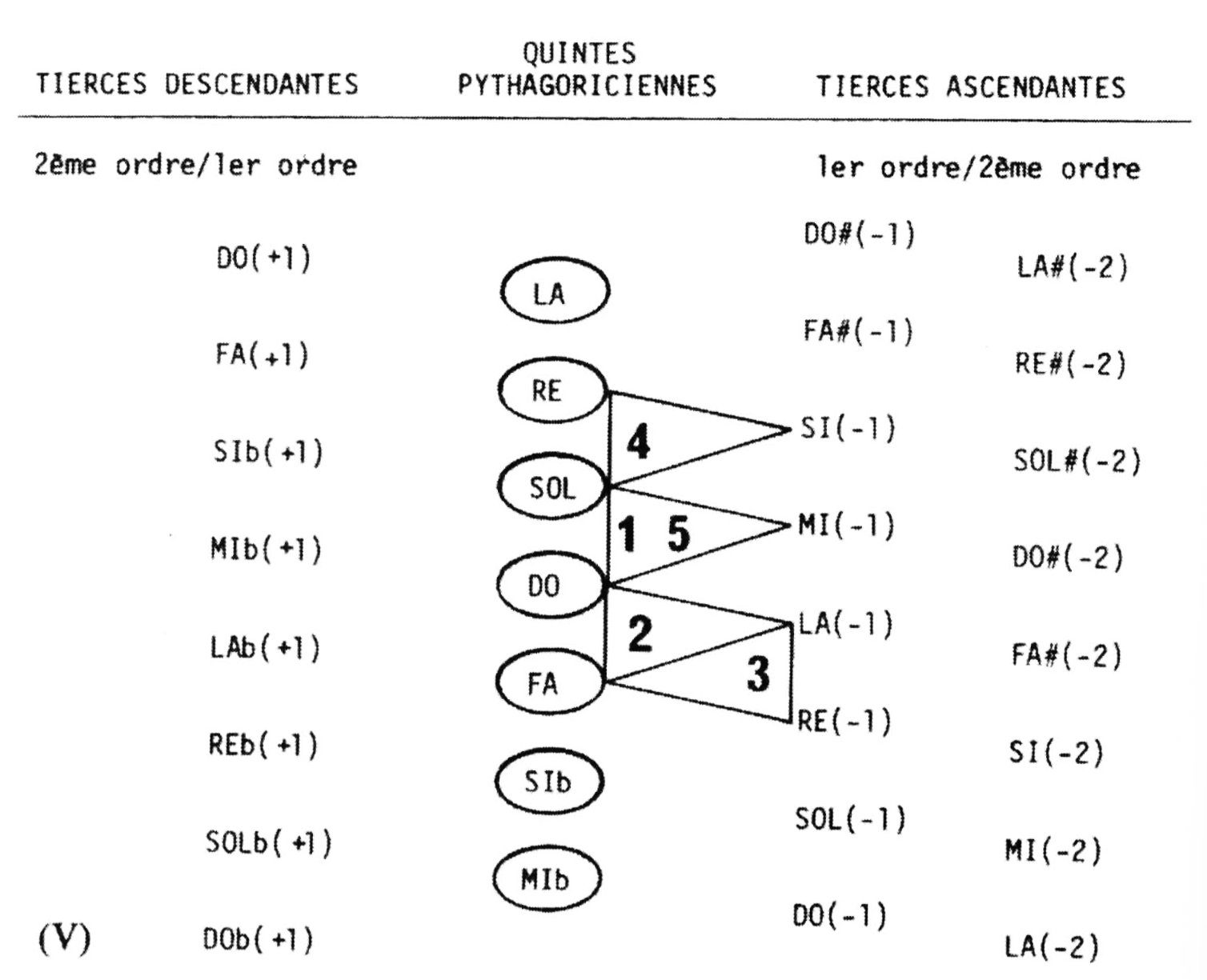
The column at the centre of this picture, with notes within ellipses, is a series of perfect fifths which Asselin called "Pythagorean".
Series of fifths are infinite. Selecting seven of them (in the middle column) creates a scale called the "global diatonic framework" (milieu diatonique global, see Asselin 2000 p. 59). In this example, the frameworks are those of "C" and "G" ("do" and "sol" in French).
Extending series of perfect fifths beyond the sixth step produces complicated ratios that can be approximated (with a schisma difference) to those produced by harmonic major thirds (ratio 5/4). Positions on the right (major third up, first order) are one syntonic comma lower than their equivalents in the middle series, and positions on the left (major third down, first order) are one syntonic comma higher.
It is possible to create more columns on the right ("DO#-2", "SOL#-2" etc.) for positions created by 2 successive jumps of a harmonic major third, and in the same way on the left ("DOb#+2", "SOLb#+2" etc.), but these second-order series are only used for the construction of temperaments — see page Microtonality.
This model produces 3 to 4 positions for each note, a 41-degree scale, which would require 41 keys (or strings) per octave on a mechanical instrument! This is one reason for the tempering of intervals on mechanical instruments, which amounts to selecting the most appropriate 12 positions for a given musical repertoire.
This tuning scheme is displayed on scale "3_cycles_of_fifths" in the "-cs.tryTunings" Csound resource of Bol Processor.

Series of names have been entered, together with the fraction of the starting position, to produce cycles of perfect fifths in the scale. Following Asselin's notation, the following series have been created (trace generated by the Bol Processor):
From 4/3 up: FA, DO, SOL, RE, LA, MI, SI, FA#, DO#, SOL#, RE#, LA#From 4/3 down: FA, SIb, MIb, LAb, REb, SOLbFrom 320/243 up: FA-1, DO-1, SOL-1, RE-1, LA-1, MI-1, SI-1, FA#-1, DO#-1, SOL#-1, RE#-1, LA#-1From 320/243 down: FA-1, SIb-1, MIb-1, LAb-1, REb-1, SOLb-1From 27/20 up: FA+1, DO+1, SOL+1, RE+1, LA+1, MI+1, SI+1, FA#+1, DO#+1, SOL#+1, RE#+1, LA#+1From 27/20 down: FA+1, SIb+1, MIb+1, LAb+1, REb+1, SOLb+1
This was more than enough to determine the 3 or 4 positions of each note, since several notes can reach the same position at a schisma distance. For example, "REb" is in the same position as "DO#-1". The IMAGE link shows this scale with (simplified) frequency relationships:
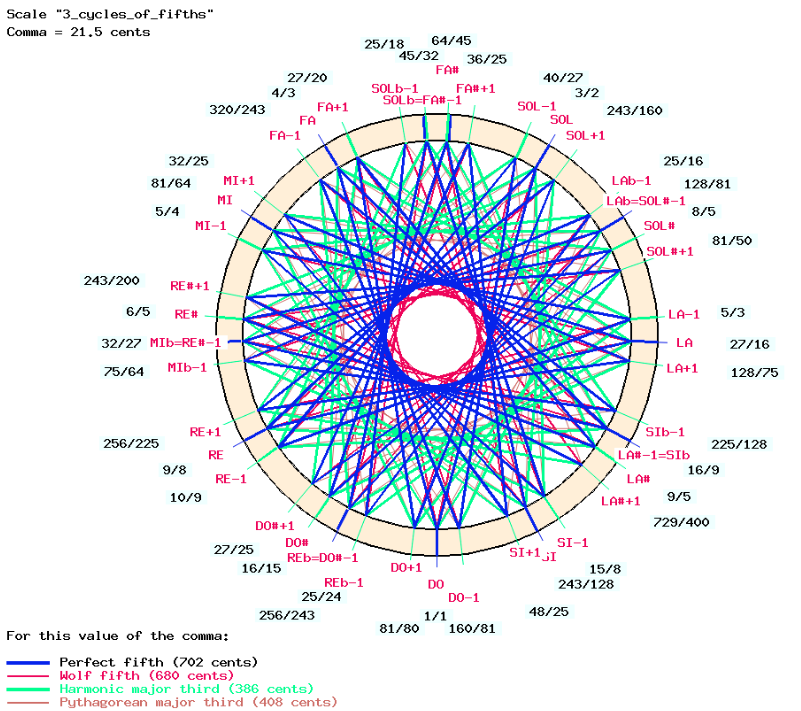
(Image created by Bol Processor)
Compared to the model advocated by Arnold (1974, see figure above), this system accepts harmonic positions on either side of the Pythagorean positions, which means that Sa ("C" or "do"), like all unaltered notes, can take three different positions. In Indian music, Sa is unique because it is the fundamental note of every classical performance of a raga, fixed by the drone (tanpura) and tuned to suit the singer or instrumentalist. However, we will see that transpositions (murcchana-s) of the basic Indian scale(s) produce some of these additional positions.
A tuning scheme based on three (or more) cycles of perfect fifths is a good grid for constructing basic chords in just intonation. For example, a "C major" chord is made up of its tonic "DO", its dominant "SOL" a perfect fifth higher, and "MI-1" a major harmonic third above "DO". The first two notes can belong to a Pythagorean series (blue marks on the graph) and the last one to a harmonic series (green marks on the graph). Minor chords are constructed in a similar way, which will be explained later.
This does not completely solve the problem of playing tonal music with just intonation. Sequences of chords must be correctly aligned. For example, should one use the same "E" in "C major" and in "E major"? The answer is "no", but the rule must be made explicit.
How is it possible to choose the right one among the 37 * 45 = 2 239 488 chromatic scales shown in this graph?
In the approach of Pierre-Yves Asselin (2000) — inspired by the work of Conrad Letendre in Canada — rules were derived from options validated by listeners and musicians. Conversely, the grama framework exposed below is a "top-down" approach — from a theoretical model to its evaluation by practitioners.
The grama framework
Using Bharata's model — see page The two-vina experiment — we can construct chromatic (12-degree) scales in which each tonal position (out of 11) has two options: harmonic or Pythagorean. This is one reason to say that the framework is based on 22 shruti-s. In Indian musicological literature, the term shruti is ambiguous, as it can mean either a tonal position or an interval.
In Bol Processor BP3 this "grama" framework is edited as follows in "-cs.12_scales":

We use lower-case labels for R1, R2 etc. and append a '_' after labels to distinguish enharmonic positions from octave numbers. So, "g3_4" means G3 in the fourth octave.
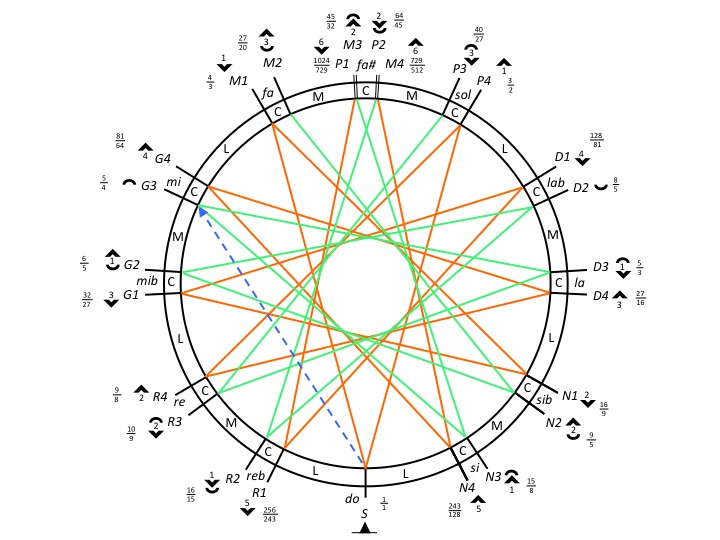
Two options for each of the 11 notes yields a set of 211 = 2048 chromatic scales. Of these, only 12 are "optimally consonant", i.e. they contain only one wolf fifth (smaller by 1 syntonic comma). These 12 scales are the ones used in harmonic or modal music to experience maximum consonance. The author(s) of Naya Shastra had this intention in mind when they described a basic 12-tone "optimal" scale called "Ma-grama". This scale is called "Ma_grama" in Csound resource "-cs.12_scales":

Click on the IMAGE link on the "Ma_grama" page to obtain a graphical representation of this scale:
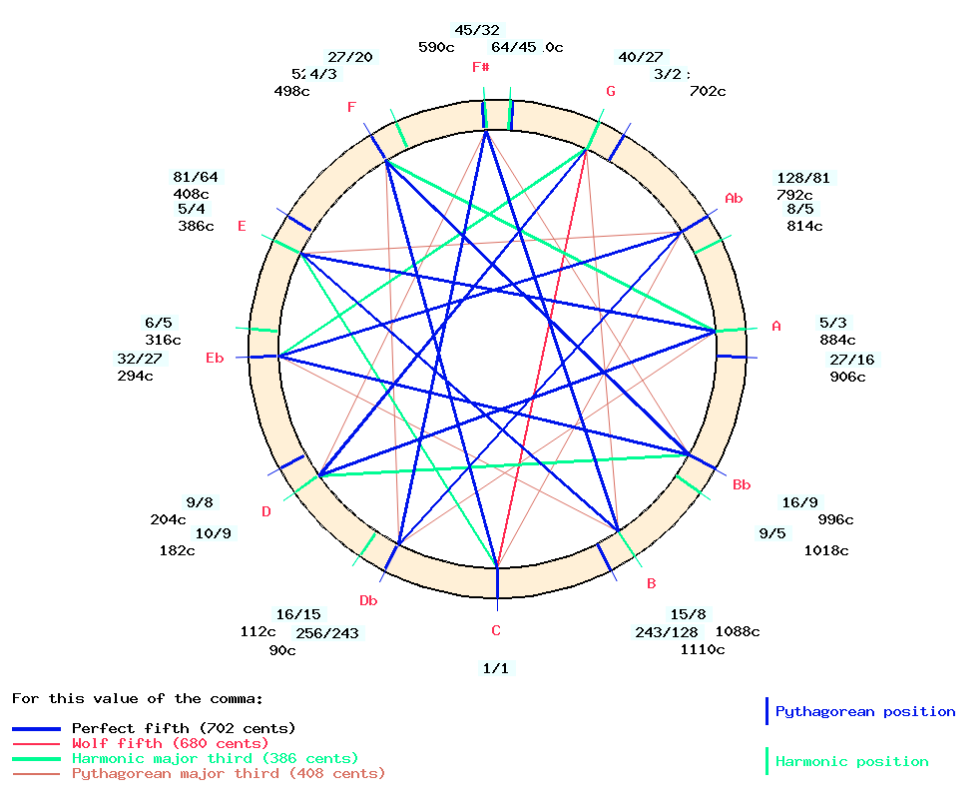
In this picture the perfect fifths are blue lines and the (unique) wolf fifth between C and G is a red line. Note that positions marked in blue ("Db", "Eb" etc.) are Pythagorean and harmonic positions ("D", "E" etc.) appear in green. Normally, a "Pythagorean" position on this framework is one where neither the numerator nor the denominator of the fraction is a multiple of 5. Multiples of 5 indicate jumps of harmonic major thirds (ratio 5/4 or 4/5). This simple rule is broken, however, when complex ratios are replaced by simple equivalents at a distance of one schisma. Therefore, the blue and green markings on the Bol processor images are mainly used to facilitate the identification of a position: a note appearing near a blue marking could as well belong to the harmonic series with a more complex ratio, bringing it close to the Pythagorean position.
It will be important to remember that all the notes of the Ma-grama scale are in their lowest enharmonic positions. Other scales are created by raising a few notes by a comma.
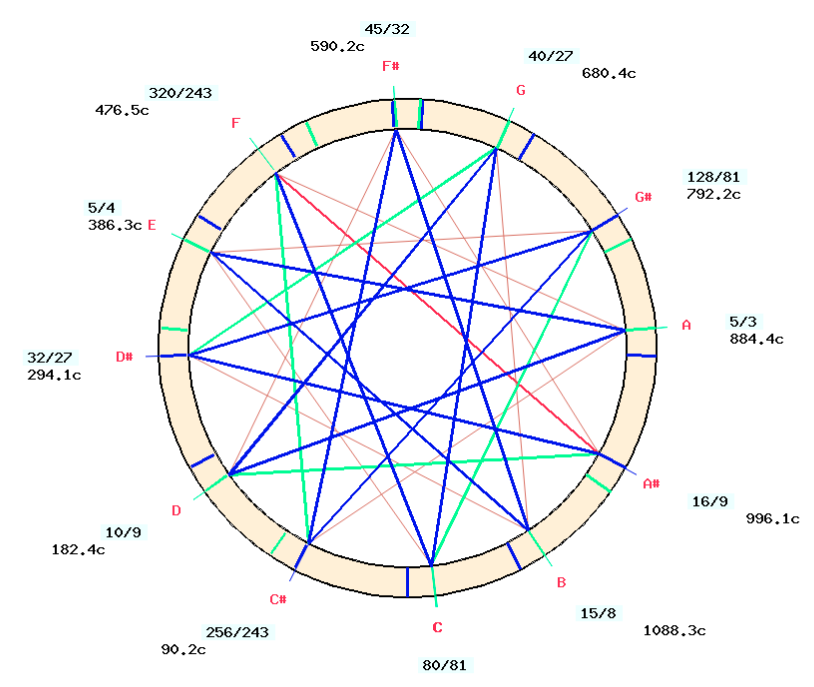
This Ma-grama is the starting point for the generation of all "optimally consonant" chromatic scales. This is done by transposing perfect fifths (upwards or downwards). The visualisation of transpositions becomes clear when the basic scale is drawn on a circular wheel which is allowed to move within the outer crown shown above. The following is Arnold's complete model, showing the Ma-Grama in the basic position, producing the "Ma01" scale:
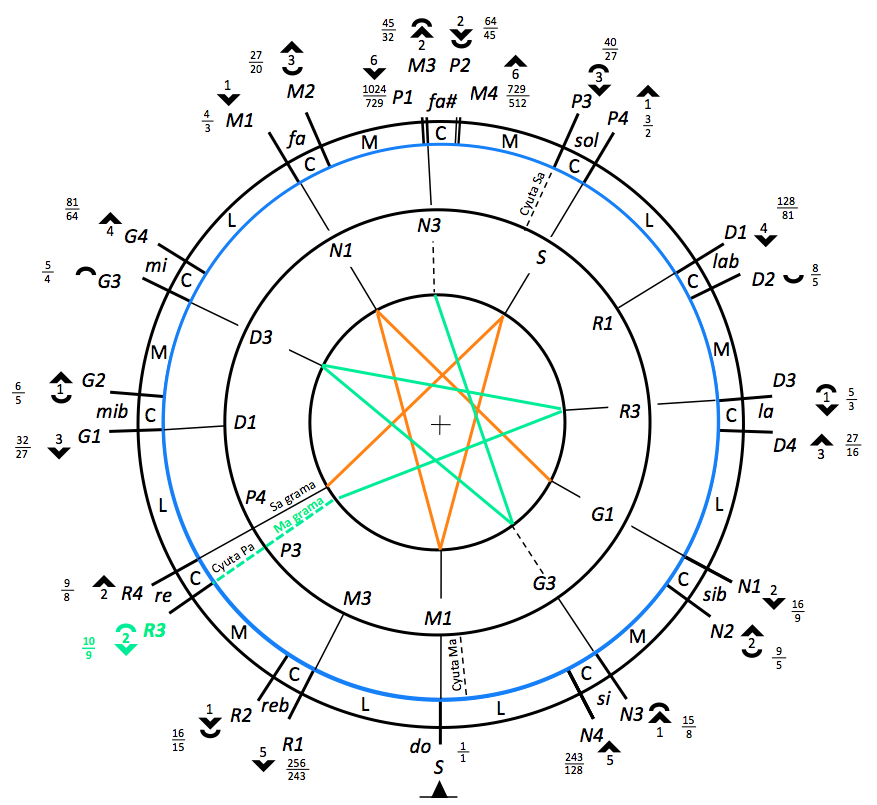
This positioning of the inner wheel on top of the outer wheel is called a "transposition" (murcchana).
Intervals are shown on the graph. For example, R3 ("D" = "re") is a perfect fifth to D3 ("A" = "la").
The "Ma01" scale produced by this M1 transposition produces the "A minor" chromatic scale with the following intervals:
C l Db c+m D c+l Eb c+m E c+l F c+m F# c+l G l Ab c+m A c+l Bb c+m B c+l C
- m = minor semitone = 70 cents
- l = limma = 90 cents
- c = comma = 22 cents
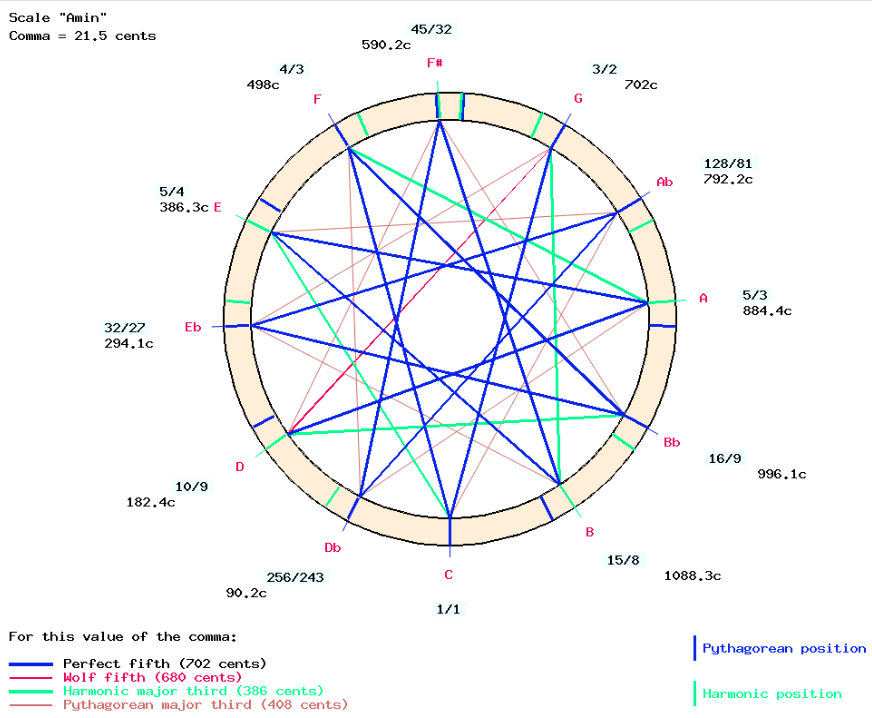
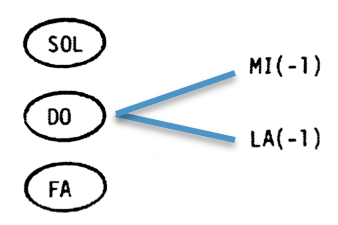
This construction of the "A minor" scale corresponds to the Western scheme for the production of just intonated chords: the fundamental "A" (ratio 5/3) is "LA-1" on the "3_cycles_of_fifths" scale, which is in the "major third upwards" series as well as its dominant "MI-1", while "C" (ratio 1/1) belongs to the "Pythagorean" series.
At first sight, the scale constructed by this M1 transposition also resembles a "C major" scale, but with a different choice of R3 (harmonic "D" ratio 10/9) instead of R4 (Pythagorean "D" ratio 9/8). To produce the "C major" scale, "D" should be raised to its Pythagorean position, which amounts to R4 replacing R3 on Bharata's model. This is done by using an alternative root scale called "Sa-Grama" in which P4 replaces P3.
P3 is called "cyuta Pa" meaning "Pa lowered by one shruti" — here a syntonic comma. The wheel representation suggests that other lowered positions may later be highlighted by the transposition process, namely cyuta Ma and cyuta Sa.
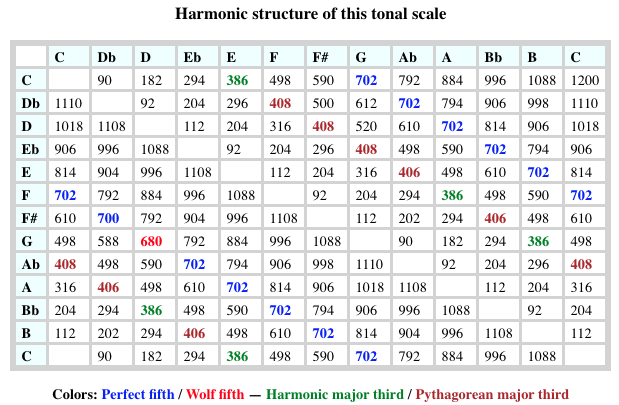
At the bottom of the "Ma01" page on "-cs.12_scales", all the intervals of the chromatic scale are listed, with the significant intervals highlighted in colour. The wolf fifth is coloured red. Note that when the scale is optimally consonant, only one cell is coloured red.
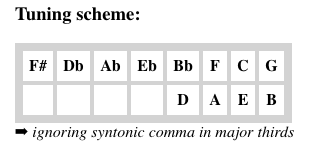
A tuning scheme is suggested at the bottom of page "Ma01". It is based on the (purely mechanical) assumption that perfect fifths are tuned first within the limit of 6 steps. Then harmonic major thirds and minor sixths are highlighted, and finally Pythagorean thirds and minor sixths can also be taken into account.

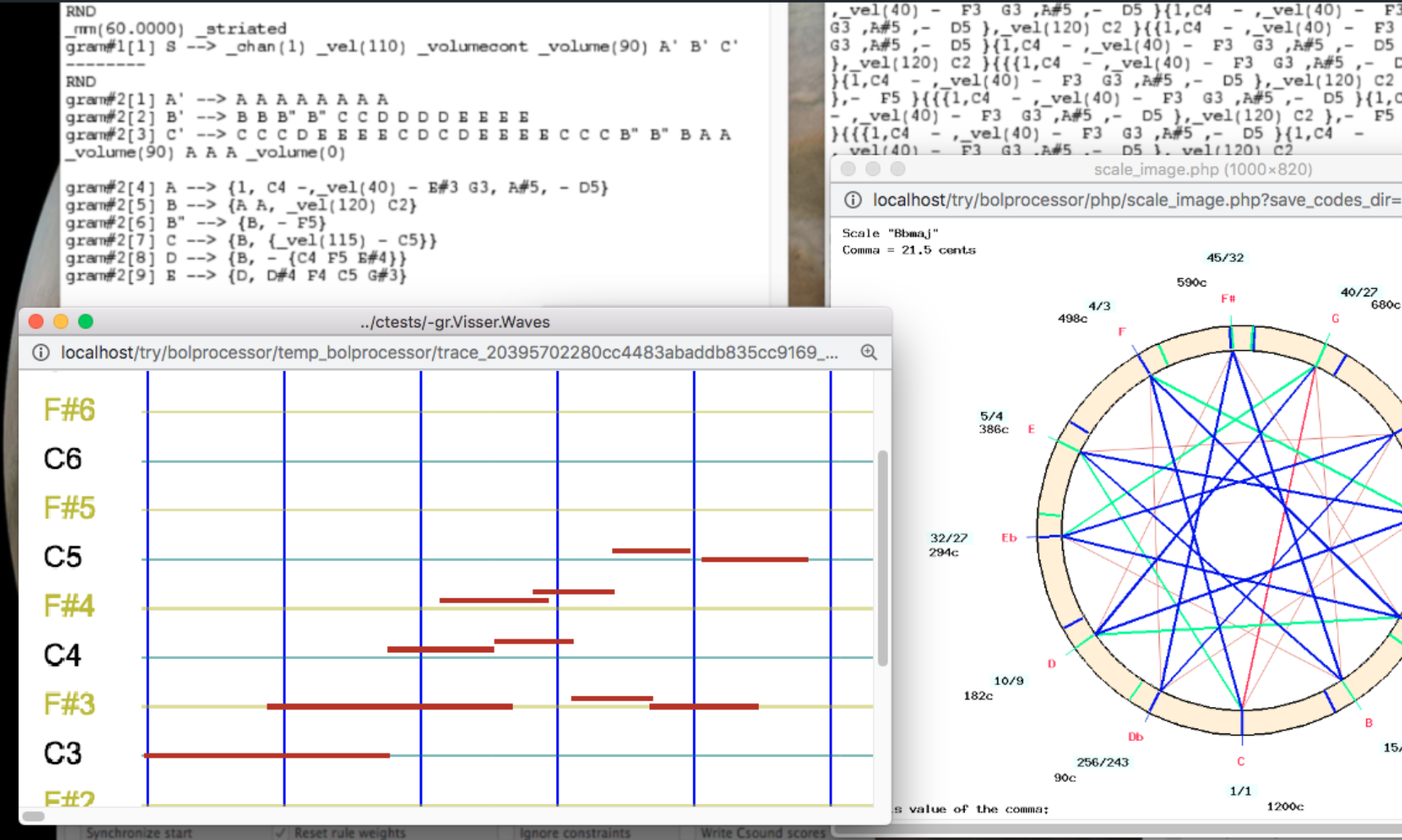
We can use "Ma01" as a 23-degree microtonal scale in Bol Processor productions because all the notes relevant to the chromatic scale have been labelled. However it is more practical to extract a 12-degree scale with only labelled notes. This can be done on the "Ma01" page. The image shows the exportat of the "Cmaj" scale with 12 degrees and a raised position of D.
Using "Cmaj" for the name makes it easy to declare this scale in its specific harmonic context. In the same way, a 12-degree "Amin" can be exported without raising the "D".
"D" ("re") is therefore the sensitive note when switching between the "C major" scale and its relative "A minor".
In all 12-degree exported scales it is easy to change the note convention — English, Italian/Spanish/French, Indian or key numbers. It is also possible to select diesis in replacement of flat and vice versa, as the machine recognises both options.
Producing the 12 chromatic scales
A PowerPoint version of Arnold's model can be downloaded here and used to check the transpositions produced by the Bol Processor BP3.

To create successive "optimally consonant" chromatic scales, the Ma-grama should be transposed by descending or ascending perfect fifths.
For example, create "Ma02" by transposing "Ma01" from a perfect fourth "C to F" (see picture). Nothing else needs to be done. All the transpositions are stored in Csound resource "-cs.12_scales". Each of these scales can then be used to export a minor and a major chromatic scale. This procedure is explained in detail on the page Creation of just-intonation scales.
Enharmonic shift of the tonic
An interesting point raised by James Arnold in our paper L'intonation juste dans la théorie ancienne de l'Inde : les applications aux musiques modale et harmonique (1985) is the comparison of minor and major scales of the same tonic, for example moving from "C major" to "C minor".
To get the "C minor" scale, we need to create "Ma04" by using four successive descending fifths (or ascending fourths). Note that writing "C to F" on the form does not always produce a perfect fourth transposition because the "F to C" interval may be a wolf fifth! This happens when going from "Ma03" to "Ma04". In this case, select, for example, "D to G".
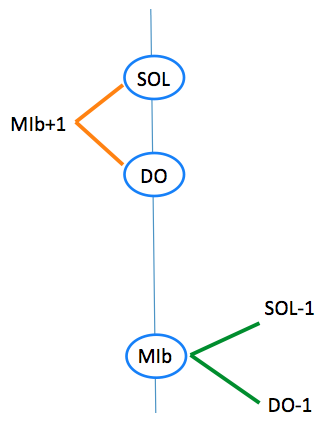
From "Ma04" we export "Cmin". Here comes a surprise:

The intervals are those predicted (see "A minor" above), but the positions of "G", "F" and "C" have been lowered by one comma. This was expected for "G" because of the replacement of P4 by P3. The bizarre situation is that both 'C' and 'F' are one comma lower than what seemed to be their lowest (or only) position in the 22-shruti model. The authors of Natya Shastra had anticipated a similar process when they invented the terms "cyuta Ma" and "cyuta Sa"…
This shifting of the base note can be seen by moving the inner wheel. After 4 transpositions, the position M1 of the inner wheel will correspond to the position G1 of the outer wheel, giving the following configuration:
This shift of the tonic was presented as a challenging finding in our paper (Arnold & Bel 1985). Jim Arnold had done experiments with Pierre-Yves Asselin playing Bach's music on the Shruti Harmonium and both liked the shift of the tonic on minor chords.
Pierre-Yves himself mentions a one-comma lowering of "C" and "G" in the "C minor" chord. However, this was one of two options predicted by his theoretical model. He tested it by playing the Cantor electronic organ at the University, and reports that musicians found this option to be more pungent — "déchirant" — (Asselin 2000 p. 135-137).
The other option (red on the picture) was that each scale be "aligned" in reference to its base note "C" ("DO"). This alignment (one-comma raising) can be done clicking button "ALIGN SCALE" on scale pages wherever the basic note ("C") is not at position 1/1. Let us listen to the "C major"/ "C minor" / "C major" sequence, first "non-aligned" then "aligned":
Clearly, the "non-aligned" version is more pungent than the "aligned" one.
This choice is based on perceptual experience, or "pratyakṣa pramāṇa" in Indian epistemology — see The two-vina experiment. We take an empirical approach rather than seeking an "axiomatic proof". The question is not which of the two options is true, but which one produces music that sounds right.
Checking the tuning system
Checking a chord sequence
The construction of just intonation using the grama-murcchana procedure needs to be checked in typical chord sequences such as the "I-IV-II-V-I" series discussed by Pierre-Yves Asselin (2000 p. 131-135):

After trying out five options suggested by his theoretical model, the author chose the one preferred by all the musicians. This is the intonation they spontaneously choose when singing, without any special instruction. This version also corresponds to Zarlino's "natural scale".
"I-IV-II-V-I" harmonic series (Asselin 2000 p. 134)
In the preferred option, the tonics "C", "F" and "G" belong to the Pythagorean series of perfect fifths, except "D" in the "D minor" chord which is one comma lower than in "G major".
In the picture, the triangles with the top pointing to the right are major chords, and the one pointing to the left is the "D minor" chord.
Asselin (2000 p. 137) concludes that the minor mode is one syntonic comma lower than the major mode. Conversely, the major mode should be one syntonic comma higher than the minor mode.
This is fully consistent with the model constructed by grama-murcchana. Since minor chromatic scales are exported from transpositions of Ma-grama with all its degrees in the lowest position, their base notes are also driven to the lowest positions. However this requires a scale "adjustment" in the cases of "Ma10", "Ma11" and "Ma12" so that no position is created outside the basic Pythagorean/harmonic scheme of the Indian system. Looking at Asselin's drawing (above), this means that no position would be picked up in the 2nd-order series of fifths in the rightmost column with two successive ascending major thirds resulting in a lowering of 2 syntonic commas. This process is explained in more detail on the page Creation of just-intonation scales.
Let us listen to the production of the "-gr.tryTunings" grammar:
S --> Temp - Just
Temp --> Cmaj Fmaj Dmin Gmaj Cmaj
Just --> _scale(Cmaj,0) Cmaj _scale(Fmaj,0) Fmaj _scale(Dmin,0) Dmin _scale(Gmaj,0) Gmaj _scale(Cmaj,0) Cmaj
Cmaj --> {C3,C4,E4,G4}
Fmaj --> {F3,C4,F4,A4}
Dmin --> {D3,D4,F4,A4}
Gmaj --> {G3,B3,D4,G4}
First we hear the sequence of chords in equal temperament, then in just intonation.
The identity of the last occurrence with Asselin's favourite choice is marked by frequencies in the C-sound score: "D4" in the third chord (D minor) is one comma lower than "D4" in the fourth chord (G major), while all other notes (e.g. "F4") have the same frequencies in the four chords.
To summarise, the tonic and dominant of each minor chord belong to the "lower" harmonic series of perfect fifths appearing in the right-hand column of Asselin's drawing reproduced above. Conversely, the tonic and dominant of each major chord belong to the "Pythagorean" series of perfect fifths in the middle column.
Checking note sequences

The rules for determining the relative positions of major and minor modes (see above) deal only with the three notes that define a major or minor chord. Transpositions (murcchana-s) of the Ma-grama produce basic notes in the same positions, but these are also chromatic (12-degree) scales. Therefore, they also establish the enharmonic positions of all the notes that would be played in that harmonic context.
Do these comply with just intonation? In theory, yes, because the 12 chromatic scales obtained by these transpositions are "optimally consonant": each of them contains no more than a wolf fifth.
In 1980, James Arnold conducted experiments to verify this theoretical model using my Shruti harmonium, which produced programmed intervals to an accuracy of 1 cent. Pierre-Yves Asselin played classical pieces while Jim manipulated switches on the instrument to select enharmonic variants.
Listen to three versions of an improvisation based on Mozart's musical dice game. The first one is equal-tempered, the second one uses Serge Cordier's equal-tempered scale with an extended octave (1204 cents, see Microtonality) and the third uses several different scales to reproduce a just intonation. To this end, variables pointing to scales based on the harmonic context have been inserted in the first grammar rules:
S --> _vel(80) Ajust Bjust
Ajust --> Cmaj A1 A2 Gmaj A3 Cmaj A4 Dmaj A5 Cmaj A6 Gmaj A7 A8 Cmaj A1 A2 Gmaj A3 Cmaj A4 Dmaj A5 Cmaj A6 Gmaj A7 A'8
Bjust --> Gmaj B1 Cmaj B2 Dmaj B3 Cmaj B4 Fmaj B5 B6 Gmaj B7 Cmaj B8 Gmaj B1 Cmaj B2 Dmaj B3 Cmaj B4 Fmaj B5 B6 Gmaj B7 Cmaj B8
Cmaj --> _scale(Cmaj,0)
Dmaj --> _scale(Dmaj,0)
Fmaj --> _scale(Fmaj,0)
Gmaj --> _scale(Gmaj,0)
… etc.
Scale comparison
At the bottom of the pages "-cs.12_scales" and "-cs.Mozart", all scales are compared for their intervalic content. The comparison is based on fractions where these have been declared, or on floating-point frequency ratios otherwise.
The comparison confirms that the "Amin" chromatic scale is identical to "Fmaj".
By raising "D" in "Ma01" we have created "Sa01", the first transposition of the Sa-grama scale. From "Sa01" we can make "Sa02" etc. by successive transpositions (one fourth upwards). But the comparator shows that "Sa02" is identical to "Ma01".
Similarly, the transpositions "Ma13", "Ma14" etc. are identical to "Ma01", "Ma02" etc. The series of chromatic scales is (as expected) circular, since "Ma13" returns to "Ma01".

For more details on frequencies, block keys, etc., see the Microtonality page.
Is this perfect?
This entire page is devoted to tonal systems defined in terms of whole-numbered ratios (i.e. rational numbers) measuring tonal intervals. There were at least two strong incentives for the idea that any "pure" tonal interval should be treated as a ratio of two whole numbers, such as 2/1 for the octave, 3/2 for a "perfect" fifth, 5/4 for a "harmonic" major third, etc.
The history of music (in the West) goes back to ideas attributed to the Greek philosopher "Pythagoras" (see above) , who believed that all things were made of [rational] numbers. This approach stumbled upon the impossibility of making the octave correspond to a series of "perfect fifths"…
As we found out — read above and The Two-vina experiment — this approach was not followed in India despite the fact that Indian scientists were significantly more advanced than the Greeks in the field of calculus (Raju C.K., 2007).
Another incentive to the use of rational numbers was Hermann von Helmholtz's notion of consonance (1877) which became popular after the period of Baroque music in Europe, following the initial claim of a "natural tonal system" by Jean-Philippe Rameau in his Traité de l'harmonie réduite à ses principes naturels (1722). The development of keyboard stringed instruments such as the pipe organ and the pianoforte had made it necessary to develop a tuning system that met the requirements of (approximately) tuneful harmony and transposition to support other instruments and the human voice. It was therefore logical to abandon a wide variety of tuning systems, especially those based on temperament, and to adopt equal temperament as the standard. By this time, composers were no longer exploring the subtleties of melodic/harmonic intervals; harmony involving groups of singers and/or orchestra paved the way for musical innovation.
Looking back to the Baroque period, many musicologists tend to believe that the tuning system advocated by J.S. Bach in The Well-tempered Clavier must have been equal temperament… This belief can be disproved by a systematic analysis of this corpus of preludes and fugues on an instrument using all the tuning systems en vogue during the Baroque period — read the page The Well-tempered Clavier.
Composers and instrument makers did not tune "by numbers", as tuning procedures were not documented (see Asselin P-Y., 2000). Rather, they tuned "by ear" in order to achieve a perceived regularity of sets of intervals: the temperament in general. This was indeed a break with the "Pythagorean" mystique, because these temperaments cannot be reduced to frequency intervals based on integer ratios.
For instance, Zarlino’s meantone temperament — read this page — is made of 12 fifths starting from “E♭” (“mi♭”) up to “G#” (“sol#”) diminished by 2/7 of a syntonic comma (ratio 81/80). The frequency ratio of each fifth is therefore
\[\ \frac{3}{2}\left(\frac{80}{81}\right)^{\frac{2}{7}}=\ 1.5\ x\ 0.99645\dots\ =\ 1.4946\dots\ \left(or\ 695.81\dots\ cents\right)\]
which cannot be reduced to an integer ratio. In the same way, the twelve intervals of the equal temperament scale are expressed in terms of irrational frequency ratios.
Overture
The goal of just intonation is to produce "optimally consonant" chords and sequences of notes, a legitimate approach when consonance is the touchstone of the highest achievement in art music. This was indeed the case in sacred music, which aimed for a "divine perfection" guaranteed by the absence of "wolf tones" and other oddities. In a broader sense, however, music is also the field of expectation and surprise. In an artistic process, this can mean departing from "rules" — just as poetry requires breaking the semantic and syntactic rules of a language…
Even when chords are perfectly consonant and conform to the rules of harmony (as perceived by the composer), note sequences may deviate from their theoretical positions in order to create a certain degree of tension or to make a better transition to the next chord.
When the Greek-French composer Iannis Xenakis - known for his formalised approach to tonality - heard Bach's First Prelude for Well-Tempered Clavier played on the Shruti Harmonium in just intonation, he declared his preference for the equal-tempered version! This made sense for a composer whose music had been praised by Tom Service for its "deep, primal rootedness in richer and older phenomena even than musical history: the physics and patterning of the natural world, of the stars, of gas molecules, and the proliferating possibilities of mathematical principles" (Service T, 2013).
Bernard Bel — Dec. 2020 / Jan. 2021
References
Arnold, E.J.; Bel, B. L’intonation juste dans la théorie ancienne de l’Inde : ses applications aux musiques modale et harmonique. Revue de musicologie, JSTOR, 1985, 71e (1-2), p.11-38.
Asselin, P.-Y. Musique et tempérament. Paris, 1985, republished in 2000: Jobert. Soon available in English.
Bel, B. A Mathematical Discussion of the Ancient Theory of Scales according to Natyashastra. Note interne, Groupe Représentation et Traitement des Connaissances (CNRS), March 1988a.
Bel, B. Raga : approches conceptuelles et expérimentales. Actes du colloque "Structures Musicales et Assistance Informatique", Marseille 1988b.
Rao, S.; Van der Meer, W. The Construction, Reconstruction, and Deconstruction of Shruti. Hindustani music: thirteenth to twentieth centuries (J. Bor). New Delhi, 2010: Manohar.
Raju, C. K. Cultural foundations of mathematics : the nature of mathematical proof and the transmission of the calculus from India to Europe in the 16th c. CE. Delhi, 2007: Pearson Longman: Project of History of Indian Science, Philosophy and Culture : Centre for Studies in Civilizations.
Service, T. A guide to Iannis Xenakis's music. The Guardian, 23 April 2013.