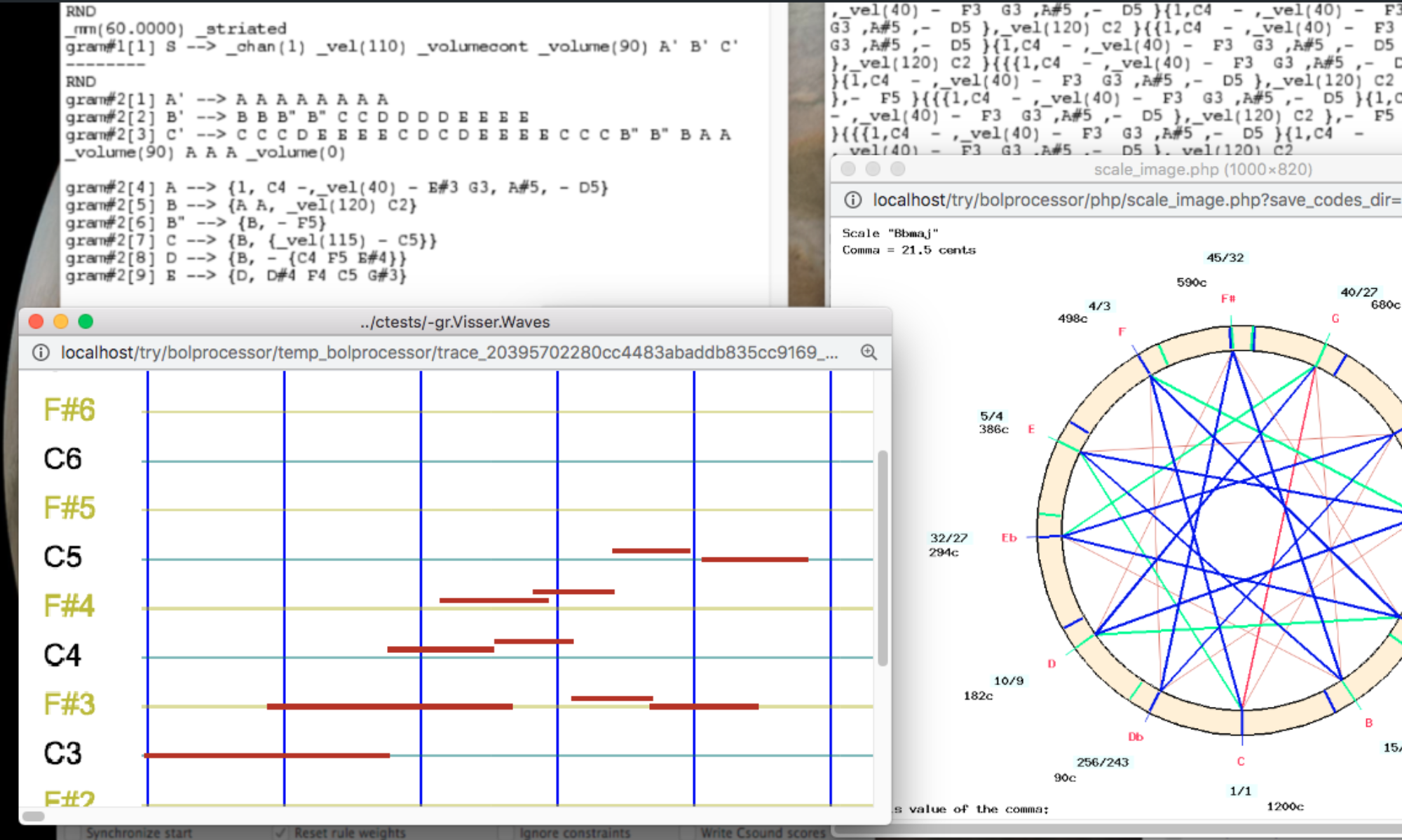
This article focuses on the Bol Processor as a tool for creating and manipulating musical scales beyond the standard twelve-tone equal temperament. It details how the software handles real-time MIDI and Csound for microtonal tuning, explaining concepts like just intonation and various historical temperaments such as Zarlino's and BACH temperament. The article also discusses the implementation of scales with more than 12 degrees, referencing ancient Indian musicology’s grama-murcchana model and demonstrating how to compare different tunings. Ultimately, the document showcases the software's flexibility in manipulating scales, and its utility for both musical composition and musicological research.
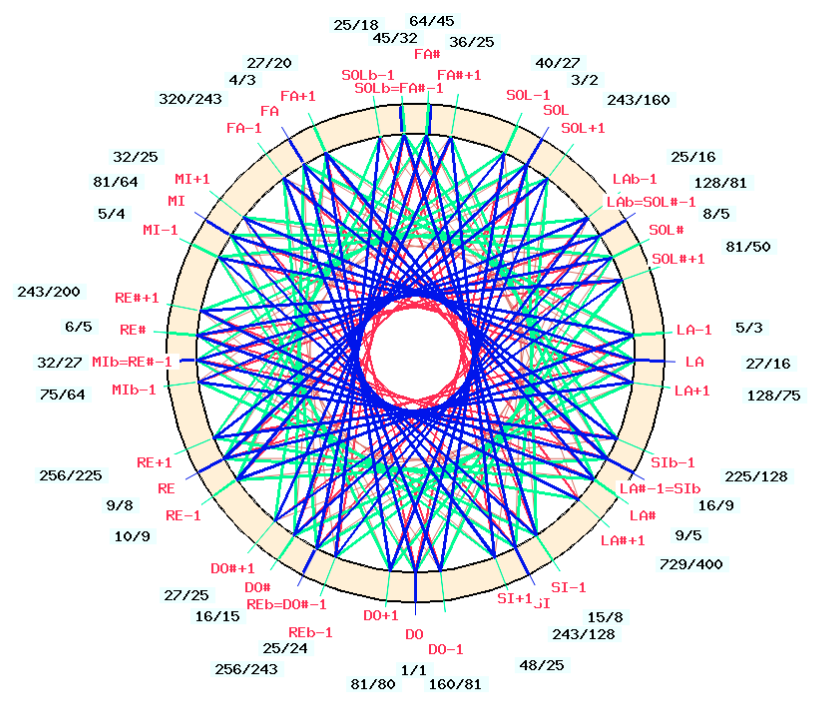
(Image created by Bol Processor)
Microtonality is a topic addressed by many musical systems that deal with tonal intervals: the use of microtones — intervals smaller than a semitone, also called "microintervals". It can also be extended to include any music that uses intervals not found in the common Western tuning of twelve equal intervals per octave. In other words, a microtone can be thought of as a note that falls between the keys of a piano tuned to equal temperament (Wikipedia).
All examples shown on this page are available in the sample set bp3-ctests-main.zip, which is shared via GitHub. Follow the instructions on page Bol Processor ‘BP3’ and its PHP interface to install BP3 and learn its basic operation.
👉 BP3 is able to handle microtonality in real-time MIDI as well as in Csound. — read the Check MIDI microtonality page for practical details.
A brief presentation
On electronic instruments such as the Bol Processor, microtonality is a matter of "microtonal tuning", here meaning the construction of musical scales alien to the conventional one(s).
Equal temperament is an intuitive model that divides the octave (frequency ratio 2/1) into 12 "equal" intervals called semitones. Each semitone has a frequency ratio of 2 1/12 = 1.059. Tonal intervals are generally expressed on a logarithmic scale, which gives the ratio 2/1 a value of 1200 cents. Each semitone is therefore worth 100 cents in a conventional scale system.
An equal tempered scale is useful for making a piece of music sound the same when transposed to another key. However, its intervals do not correspond to the (presumably) "natural" intervals constructed from whole-number frequency ratios using the numbers 3, 4, 5. These simple ratios give the impression of consonance because the frequencies of the upper partials (harmonics) can coincide: if two strings vibrate at a frequency ratio of 3/2 (a "perfect fifth"), the 3rd harmonic of the lowest vibration is at the same frequency as the 2nd harmonic of the higher vibration.
In an equal tempered scale, the harmonic major third (C-E) of 400 cents has a ratio of 1.26 instead of 1.25 (5/4). The major fifth (C - G) also sounds slightly "out of tune" with a ratio of 1.498 instead of 1.5 (3/2). These mismatches can produce beats that are considered unpleasant in harmonic contexts.
When tuning stringed instruments (such as the piano), octaves can be stretched a little to compensate for a slight inharmonicity of the upper partials produced by vibrating strings (in higher octaves), as advocated by Serge Cordier. A value of 1204 cents sounds fair, with the added advantage of making fifths sound "perfect" in a 3/2 ratio. With this setting, the frequency ratio of the stretched octaves is 2(1204/1200) = 2.0046. This effect can be reproduced in electronic instruments such as digital pianos that imitate mechanical ones. We will see how it can be implemented in the Bol Processor BP3.

Musicologists agree that equal temperament was never exactly achieved on classical instruments such as pipe organs and harpsichords. Rather, instrument tuners have developed rules for reproducing the most pleasing intervals in particular musical contexts. In other words, a mechanical instrument should be tuned according to a style and repertoire of music. Pierre-Yves Asselin (2000) has published a detailed compilation of tuning techniques used by European musicians and instrument makers over the past centuries — listen to examples on the page Comparing temperaments. The same flexibility can be achieved with sounds produced by "algorithms".
Outside of Western classical music, a wide variety of tonal systems deliberately reject 12-tone-per-octave tonality. Arabic-Andalusian music is often described as a "quartertone" system, which divides the octave into 24 intervals. Equal tempered scales of 7 degrees have been identified on various traditional African instruments. The grama-murcchana theoretical model of tonal music in India claims the use of 22 shruti-s, presumably microintervals of unequal size (see below).
Many unconventional systems have been invented and applied to contemporary music, often departing from octave-repeating scales. See for, example, the Bohlen-Pierce scale, which is based on a 3/1 interval (a "tritave") divided into 13 grades/notes — see the MIDI microtonality page. All these scales can be implemented in the Bol Processor.
The scale() operator in Bol Processor BP3
We'll be discussing the use of scales in the context of Csound, although the same is possible in the real-time MIDI and MIDI file environment — read this page. When using MIDI, the machine recognises that MIDI microtonality mode is required as soon as it sees a "scale()" operator. If a tonal resource (a "-to" file) is specified in the grammar or data, all scales listed in the resource will be accessible.
For geeks: Csound scores are flexible in the way they represent tonal positions. A common convention is the octave point pitch class. For example, the note "A4" would be assigned the tonal position "8.09", meaning that it is the 9th note in the 8th octave (in the English convention). This value produces a note at the diapason frequency (usually 440 Hz) on a Csound instrument.
It is also possible to specify the note position by its frequency in cycles per second (cps mode). This allows a high level of accuracy as frequencies are expressed in floating point format. For example, "A4" is equivalent to "440.0". Accuracy better than 1‰ is not noticeable.
As explained on page Csound tuning in BP3, it is possible to send notes in both the octave point pitch class and cps formats to the same Csound instrument.
In fact, microtonal scores will only use cps. The cps mode is also used by BP3 whenever the diapason frequency is not exactly 440 Hz. To make all frequencies visible on Csound scores, for example, set the diapason to "400.01"…
Let us take a simple example to demonstrate the use of multiple scales. The grammar is:
-se.tryScales
-cs.tryScales
-to.tryScales
ORD
S --> _scale(0,0) C4 E4 A4 {8,{C4,E4,G4,C5}} {8,{C4,Eb4,G4,C5}} - _scale(piano,C4) C4 E4 A4 {8,{C4,E4,G4,C5}}{8,{C4,Eb4,G4,C5}} - _scale(just intonation,C4) C4 E4 A4 {8,{C4,E4,G4,C5}} {8,{C4,Eb4,G4,C5}}
In this grammar, the same sequence is repeated three times in different tunings:
- _scale(0,0) is the default tuning = 12-degree equal-tempered
- _scale(piano, C4) refers to the "piano" scale
- _scale(just intonation, C4) refers to a (so-called) "just-intonation" scale
Note "C4" appearing in these operators is the block key, here meaning the key that must correspond to its equal temperament value in the tuning set by the scale.
It may be necessary to listen several times to notice subtle differences:
The sound is produced by the Csound instrument "new-vina.orc" designed by Srikumar Karaikudi Subramanian to imitate the Sarasvati vina, a long-stringed instrument played in South India — listen to his demo: Sarasvati vina. This type of instrument is capable of highlighting the finest tonal subtleties.
Beats are audible in the equal-tempered version, but slightly less so in the piano version, and almost absent in the just-intonation rendering. Looking at the Csound score makes it easy to check theoretical models:
In the Csound score, note names have been automatically replaced with their translations in the definitions of scales piano and just intonation (see below). For example, in the piano scale of this example, 'C4', 'D4', 'E4'… have been replaced by 'do3', 're3', 'mi3' with an additional 'p' marker: 'dop3', 'rep3', 'mip3'…
In the same way, just intonation notes are labelled 'Cj4', 'Dj4', 'Ej4' etc. This renaming is optional since all these scales are made up of 12 degrees with identical key positions, but it is used here to make the Csound score more explicit.
The use of "C4" as a block key means that it is always played at a frequency of 261.630 Hz. Consequently, "A4" is at 440 Hz in the first occurrence and a little higher in the piano version due to the octave stretching with a ratio of 524.463 / 261.630 = 2.0046, which is 1204 cents.
Finally, we notice that, as predicted by the model, the perfect major fifth (C - G) produces the same positions (392.445 Hz) in the piano and just intonation scales.
In reality, the "just intonation" fragment in this example would be out of tune if we follow the framework of tonality proposed by Asselin (2000) and confirmed by an extension of the ancient grama-murcchana system in India. In the last "C minor" chord {C4, Eb4, G4, C5}, the notes "C4", "C5" and "G4" should be lowered by a syntonic comma. This means that playing "just intonation" in Western harmony requires more than a single just-intonation scale: each harmonic context requires its own specific tuning, which indeed cannot be achieved on keyboard instruments. A method for constructing just-intonation scales and using them in Bol Processor music is given on the Just intonation: a general framework page.
Looking at two scales
From the grammar page "-gr.tryScales" we can follow the tonal resource file "-to.tryScales" which contains scale definitions. Csound instrument definitions are contained in "-cs.tryScales", along with the instruction
f1 0 256 1 "vina-wave-table.aiff" 0 4 0
telling the Csound instrument to use the "vina" waveform. From August 2024, tonal resources and Csound instruments are stored in separate files, as microtonality is no longer reserved for Csound.
The following is a representation of the piano scale (Cordier's equal temperament):
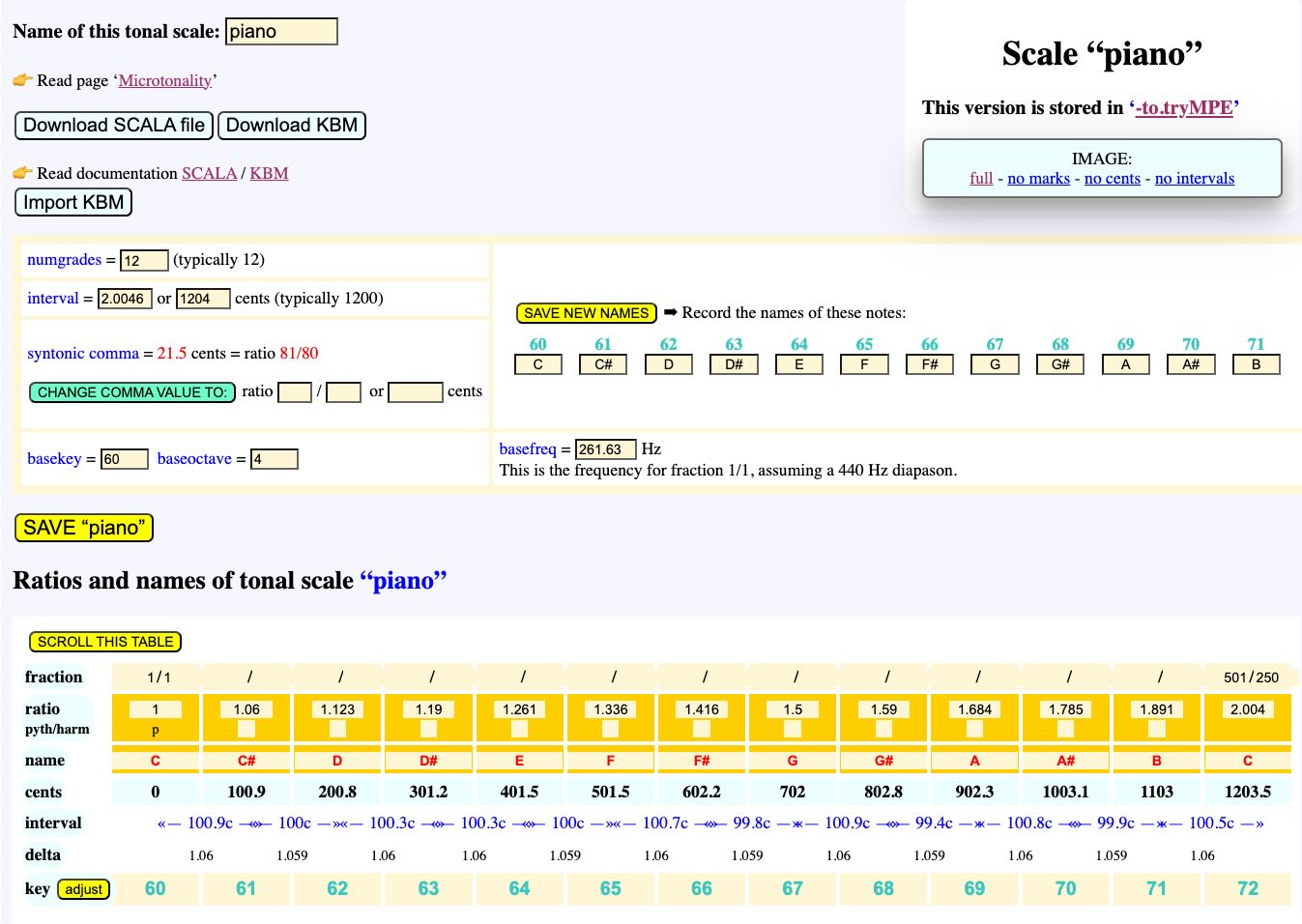
Note buttons for export/import of SCALA and KBM files.
All the intervals were set in a single click, after entering "1204" as the size of the octave in cents, which set the last ratio to 2.004 (approximately 501/250). The "INTERPOLATE" button was then clicked to calculate the intermediate ratios.
The scale is displayed as a circular graph by clicking on the "IMAGE" link:
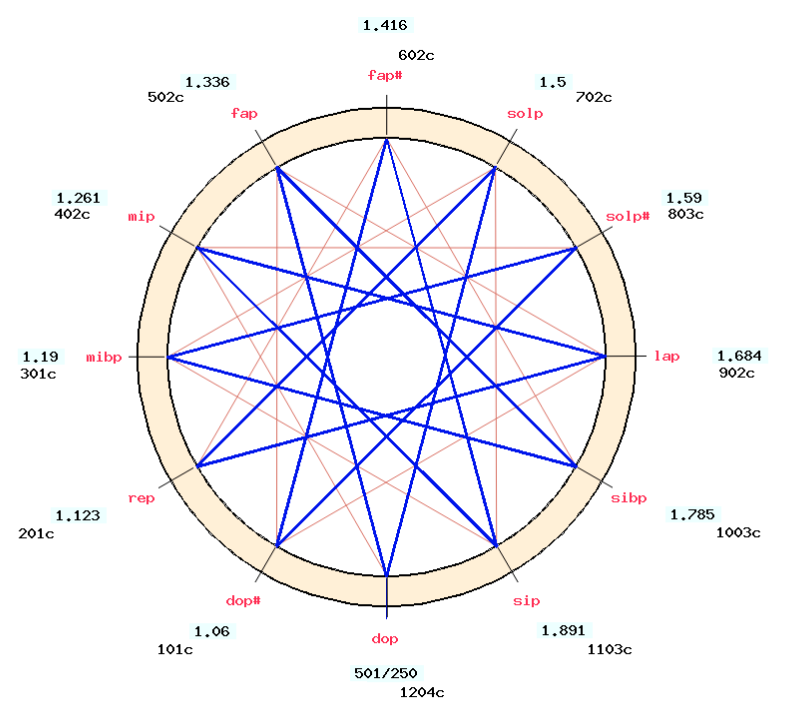
The display confirms that the position of "G" ("solp") is in the ratio 3/2 or 702 cents. However, the tonal distance between "G" ("solp") and "D" ("rep") is slightly smaller (699 cents), which means that this scale is not a pure cycle of fifths, as the latter would have ended after 12 steps with an octave extended by a Pythagorean comma (scale "twelve_fifths" in "-to.tryScales"):
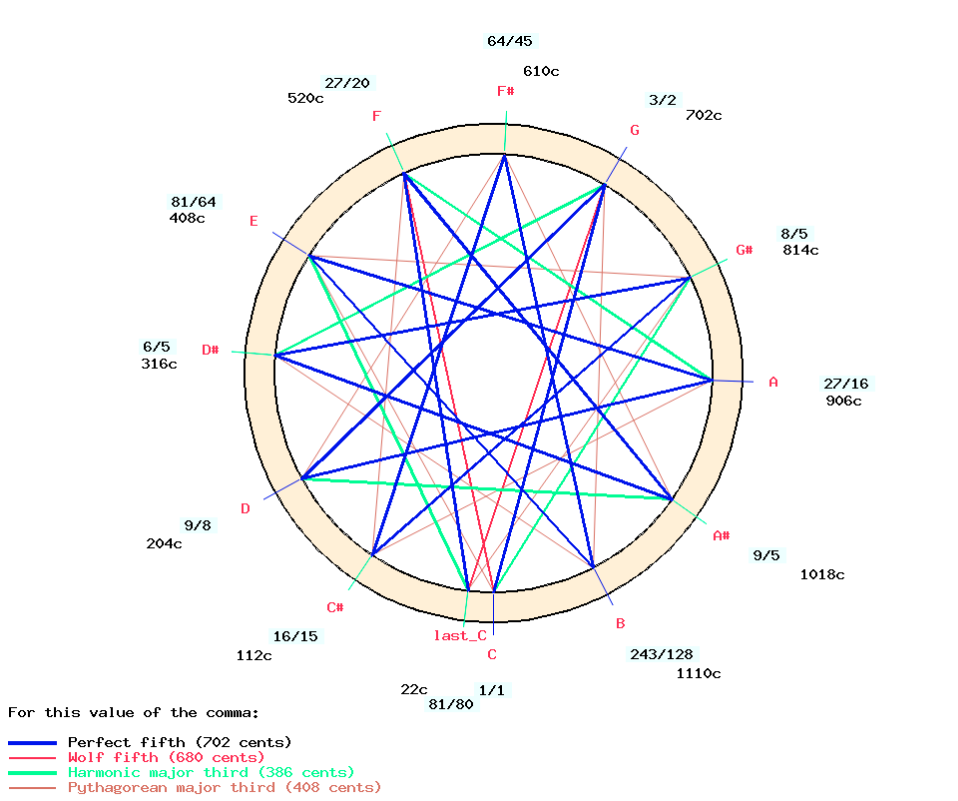
The basekey is the key used to produce basefreq. Here basefreq is set to 261.630 Hz for key #60 which is usually the "middle C" on a piano keyboard. The basefreq parameter has an effect on the pitch which is further adjusted by the value of the diapason entered in "-se.tryScales". If the diapason is set to 430 Hz, the frequency of "C4" would be 261.630 x 430 / 440 = 255.68 Hz.
The baseoctave parameter is not stored in the Csound function table, but it is required by the Bol Processor to name notes correctly. This scale uses the Italian/French note convention, where key #60 is called "do3" instead of "C4". Therefore baseoctave = 3.
Temperament
At the bottom of the "Scale" page is a form for constructing scales in musical temperament. The scope of this procedure is wider than usual because the interface permits the modification of any series of intervals, not just fifths and fourths.
Bol Processor procedures for the production of tempered scales (and all scales in general) can be used both to visualise/hear intervals and chords derived from a theoretical description of the scale, and to check that a procedure for tuning a mechanical instrument conforms to its theoretical description. Below is an example of both approaches applied to Zarlino's meantone temperament (tempérament mésotonique).
The long history of the temperament in European music is covered in Pierre-Yves Asselin's dissertation and publication (2000, p. 139-150). During the 16th and 17th centuries, European musicians tended to prefer "pure" major thirds (frequency ratio 5/4) at the cost of compromising the size of the fifths. This was called the "pure third meantone temperament" (tempérament mésotonique à tierces majeures pures) which was generally achieved by reducing the size of certain fifths by a fraction of the syntonic comma (Asselin 2000 p. 76). After this period, there was another fashion of using perfect fifths (frequency ratio 3/2) and compromising the size of major thirds in the same way. Both methods — and many more — are implemented in the Bol Processor. Algorithmic tuning is indeed easier to achieve than tuning a mechanical instrument!
Zarlino, theory
Let us try Zarlino's meantone temperament (Asselin 2000 p. 85-87) which was popular in the 16th and 17th centuries. It consists of 12 fifths starting from "E♭" ("mi♭") up to "G#" ("sol#") diminished by 2/7 of a syntonic comma — that is 6 cents.
➡ This should not be confused with Zarlino's "natural scale", an instance of just intonation.

Theoretically, this takes two steps from the previously known position "C".
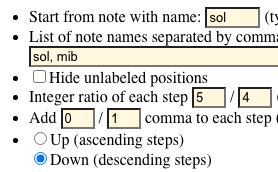
First, we enter the starting note "do" and the sequence of fifths "do, sol, re, sol#," specifying a ratio of 3:2 with a -2/7 comma modification (see picture).

Then we do the same with fourths (descending fifths) starting from "do" ("C") down to "mi♭" ("E♭").
The result is displayed by clicking on the IMAGE link:
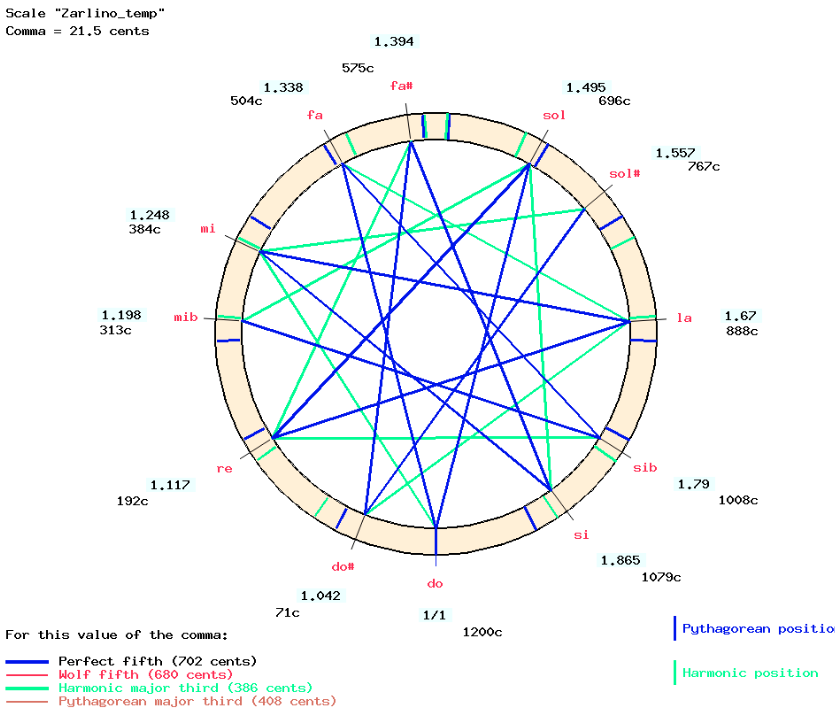

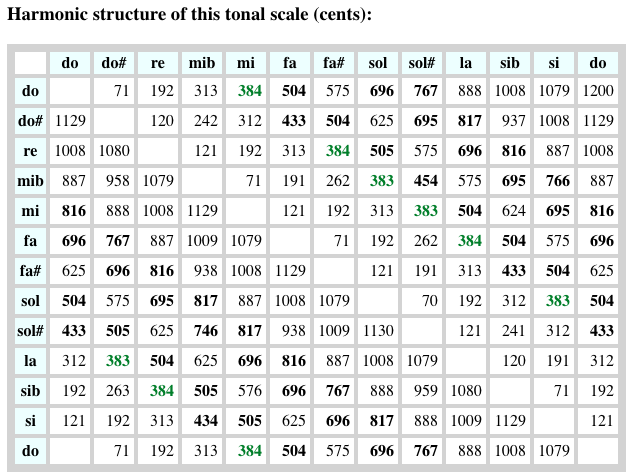
In this temperament, the harmonic major thirds (green connections on the graph) are equal and slightly smaller (384 cents) than the "pure" ones (ratio 5/4 or 386 cents). Semitones between unaltered and altered notes are equal (71 cents). All major tones are equal (192 cents) except "do#-mi♭" and "sol#-sib" (242 cents).
Noticeable dissonances are found in the "sol#-mi♭" fifth (746 cents, i.e. an extra 2 + 1/7 commas = 44 cents) and major thirds such as "sol#-do", "do#-fa", "fa#-sib" and "si-mi♭" which are larger (433 cents) than Pythagorean major thirds (408 cents). Obviously, these intervals are not intended to be used in the musical repertoire to which this tuning is applied…
Comparison
A layperson might wonder whether small tonal adjustments — often less than a quarter of a semitone (i.e. 25 cents) — have any noticeable effect on musical works using these tuning systems. Comparative experiments are easy with the Bol Processor.
For example, let us play one (of a billion variations) of Mozart's musical dice game, with tuning options selected by activating a first rule in "-gr.Mozart":
// gram#1[1] S --> _vel(80)_tempo(3/4) _scale(0,0) A B // Equal temperament
// gram#1[2] S --> _vel(80) _tempo(3/4) _scale(piano,0) A B // Equal temperament (Cordier)
// gram#1[3] S --> _vel(80) _tempo(3/4) _scale(Zarlino_temp,0) A B // Zarlino's temperament
// gram#1[4] S --> _vel(80) _tempo(3/4) Ajust Bjust // Just intonation
Musical productions are listed below. The random seed has been set to 998 (in "-se.Mozart") as this variation contains a greater number of chords, and the performance has been slowed down by "_tempo(3/4)".
It is important to remember that of these options, only the first three ones (temperaments) are accessible on fixed-pitch MIDI instruments with 12-degree keyboards. The last one (just intonation) requires a "retuning" of each harmonic content, which is possible if the instrument accepts pitchbender corrections — see page MIDI microtonality.
The first option (equal temperament) is the default tuning of most electronic instruments:
The second option is an equal temperament with octaves stretched by 4 cents, as advocated by Serge Cordier (see above):
The third option is Zarlino's temperament:
The last option is "just intonation":
Zarlino: a simulation of physical tuning
The tuning of mechanical instruments (such as a harpsichords) requires different procedures from the programming of "tempered" scales on the Bol processor. However, by using the computer, it is possible to quickly verify that the mechanical procedure would produce the expected result. Let us demonstrate this using Zarlino's temperament.
On the computer we had programmed a series of 7 ascending fifths diminished by a 2/7 comma from "do" to "do#". This is impossible to achieve "by ear" on a mechanical instrument. Pierre-Yves Asselin (2000 p. 86) revealed the method shown below.

First step
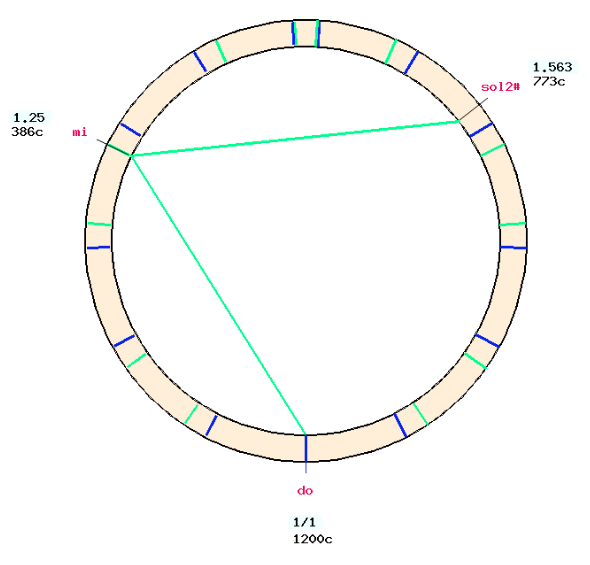
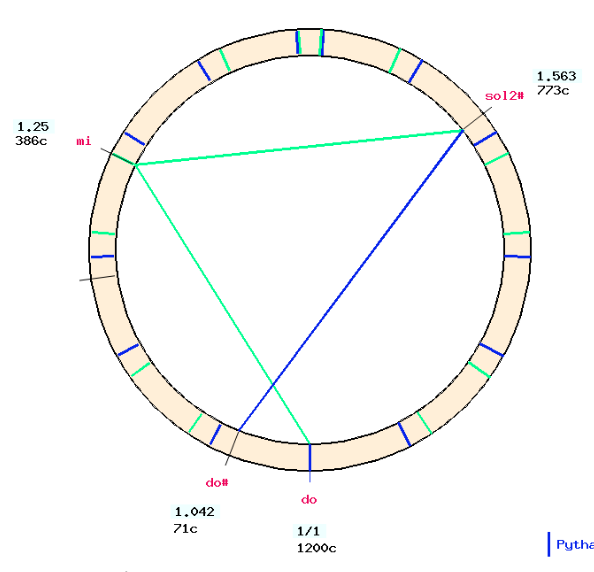
From "do", tune two successive major thirds. This results in a "sol#" which is positioned at a frequency ratio of 25/16 (773 cents) above "do".
This "sol#" is actually "SOL#+2" of the 2nd order harmonic fifths down series in Asselin's tuning framework (2000 p. 62) — see page Just intonation: a general framework. It is not exactly the one expected on Zarlino's meantone temperament, although it is close. It is labelled "sol2#".

Second step
From "sol2#" tune down a perfect fifth, resulting in "do#".
Be careful to program a perfect fifth, which is specified on the form as "add 0/1 comma". There is also a form for creating series of perfect fifths which can be used for this step.
The resulting "do#" (ratio 1.04166) is exactly 52/3/23, as expected in Zarlino's meantone temperament (Asselin 2000 p. 194).
Third step

Tune 7 equal fifths between "do" and "do#". Equalising fifths is a typical procedure for tuning mechanical instruments. Notes "sol", "re", "la", "mi", "si", "fa#" will be created. Here we specify that all intervals need to be close to the fraction 3/2, even though they will end up as fifths diminished by a 2/7 comma since we clicked the EQUALIZE INTERVALS button.
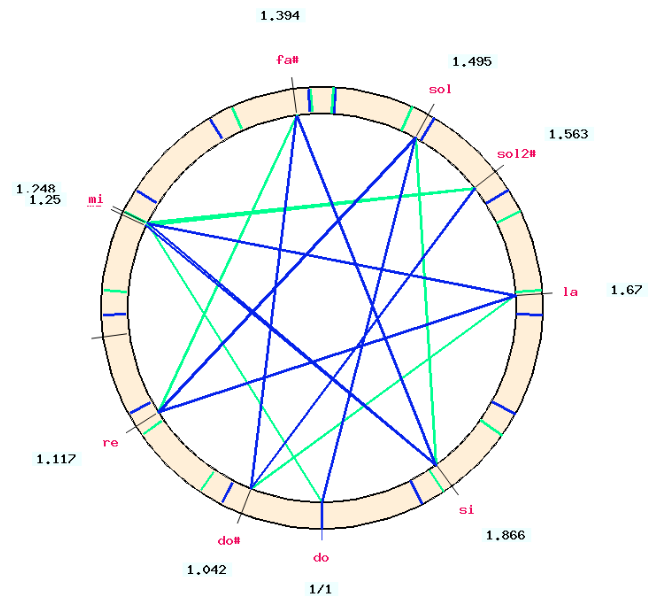
The missing notes "sol", "re", "la", "si", "fa#" are created. For the existing note "mi", the machine checks that its current position is close to the one predicted by the approximate fraction.
The graph shows that the calculated position of "mi" (ratio 1.248) is slightly different from its previous position (1.25), but this difference is negligible. We keep both positions on the graph, knowing that only one will occur in a physical tuning.
Fourth step
Now tune down 3 fifths from "do" to "mi♭", diminished by a 2/7 comma. This can be done by reproducing "by ear" intervals created in the previous step. Another method is to tune "mi♭" a harmonic major third below "sol" as shown on the form.
Fifth step

Once "mi♭" has been tuned we can tune three equal fifths (in fact diminished by 2/7 comma) between "mi♭" and "do". Again we use the "equalize intervals" procedure. At this stage, the positions of "si♭" and "fa" are created.
The result is shown in the graph below:
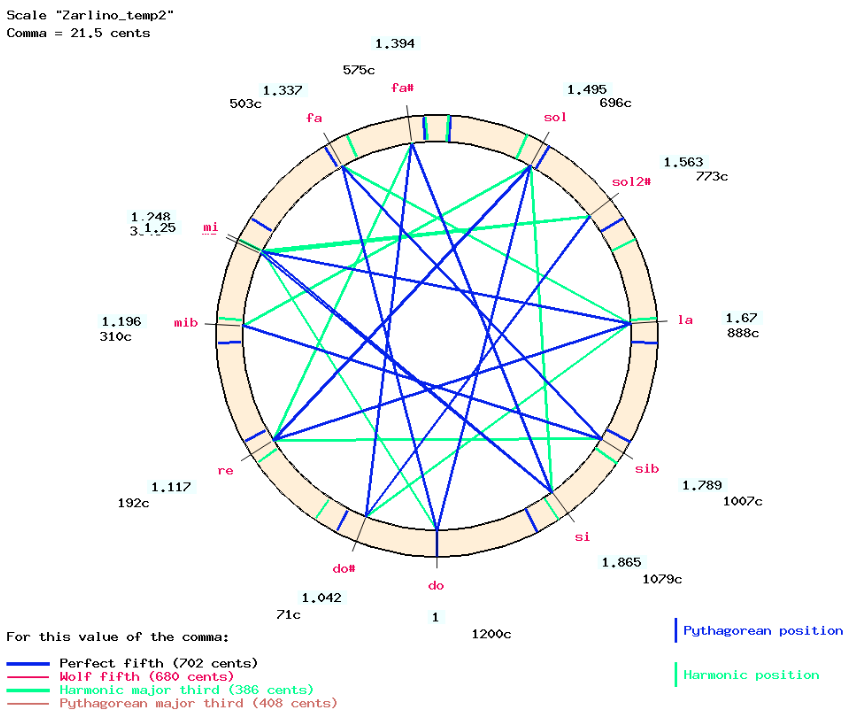
On this graph, the ratio 1.563 for "sol#" is close (within 7 cents) to 1.557 of Zarlino's temperament. On a mechanical instrument, since "mi" tuned by equalising fifths (3d step) was at position 1.248, adjusting the "mi-sol#" major third to a 5/4 ratio would set "sol#" at a better ratio (1.56).
More temperaments
All the temperaments listed in Asselin's thesis can be easily programmed on the Bol Processor. Take, for example, a classical meantone tuning (Asselin 2000 p. 76), popular in the 16th and 17th centuries, also known as Chaumont (Asselin 2000 p. 109). Its aim is to produce "pure thirds" (ratio 5/4). It consists of a series of fifths from "mi♭" ("E♭") to "sol#" ("G#") diminished by a 1/4 comma. The problem is that the tuning scheme — unlike Zarlino's meantone — does not start from "do" ("C"). There are two solutions.
The first solution is to divide the series of fifths into two parts: first create the series "do, sol, re, la, mi, si, fa#, do#, sol#" of ascending fifths, then the series "do, fa, si♭, mi♭" of descending fifths.

In the second solution, we directly create the series "mi♭, si♭, fa, do, sol, re, la, mi, si, fa#, do#, sol#" of ascending fifths, giving the graph shown below.
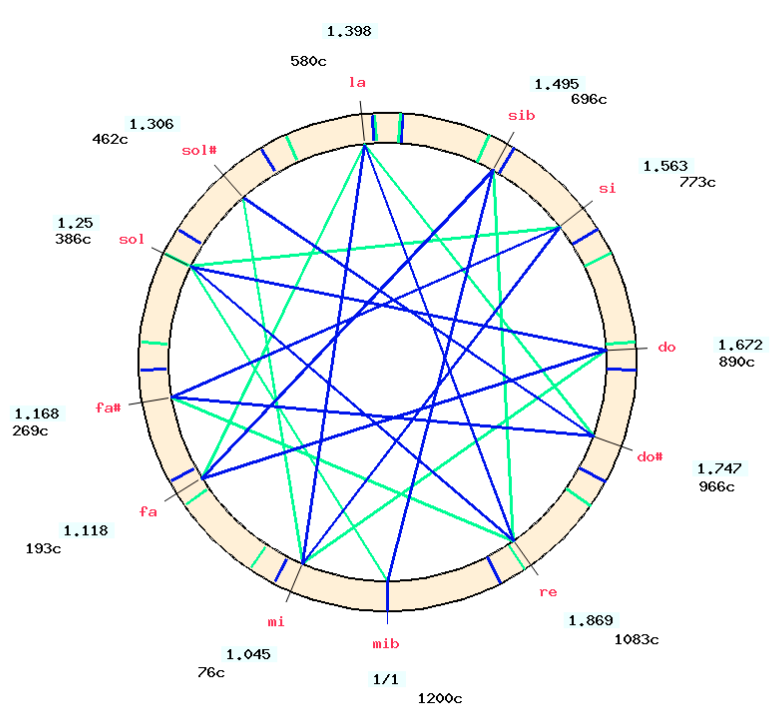
This tuning is correct but it cannot be used by the Bol Processor console because of the shift of the reference. Complicated procedures would be required to set the diapason (A4 frequency) to the desired standard and to assign the correct key numbers to the notes of the scale.
Fortunately, this problem is solved in a single click by resetting the base of the scale to note "do", which amounts to a rotation of the graph.
We take this opportunity to replace the Italian/French note convention with the English note convention.
The result is the classic meantone scale tuning which is notable for its large number of harmonic major thirds (circa 5/4, green lines):
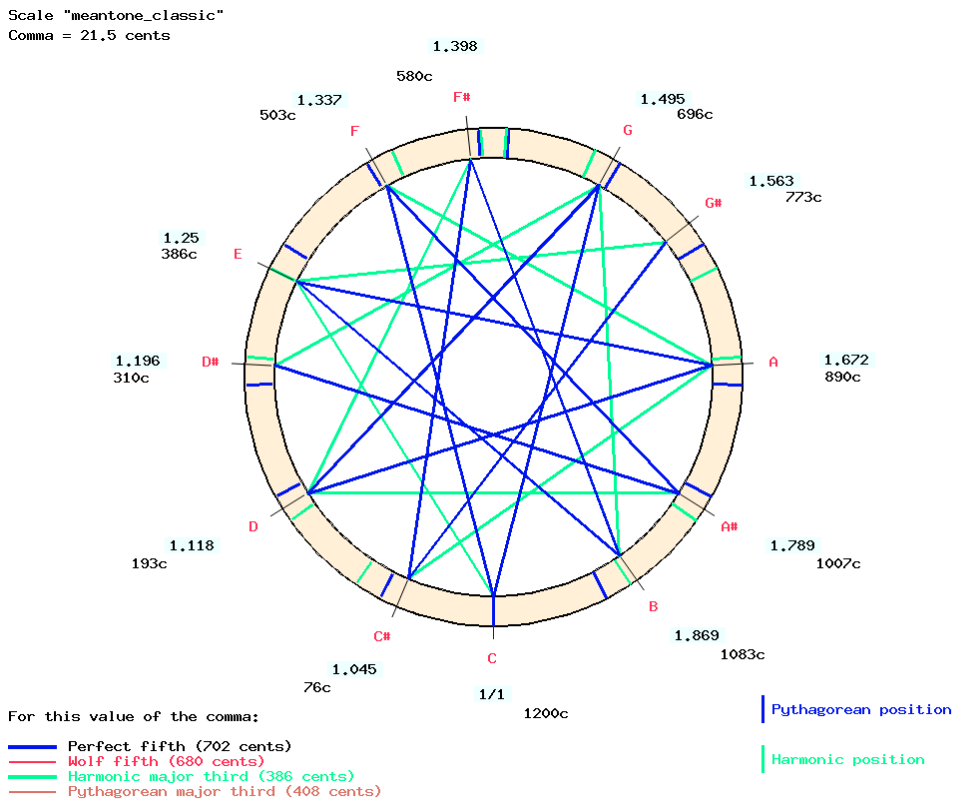
The same methods can be used to implement another meantone temperament popular at the same time (16th-17th century) which aims to enhance pure minor thirds (Asselin 2000 p. 83). It can also be described as a series of ascending fifths from "mi♭" to "sol#" with a different adjustment: the fifths are diminished by 1/3 comma.
In this tuning, the minor thirds are sized 316 cents (harmonic minor third, frequency ratio 6/5) with the exception of "A#-C#", "D#-F#" and "F-G#" which are all 352 cents:
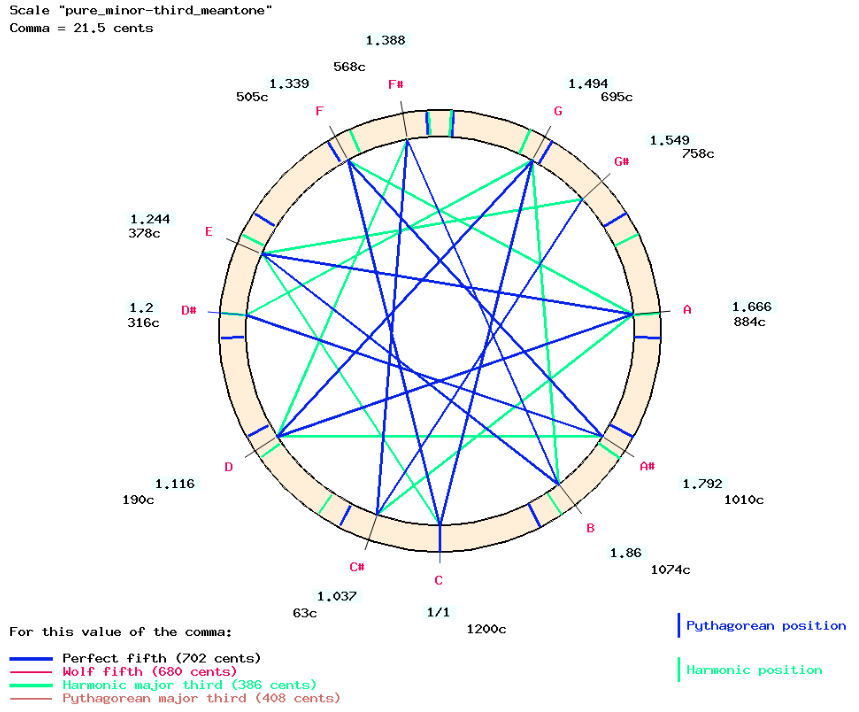
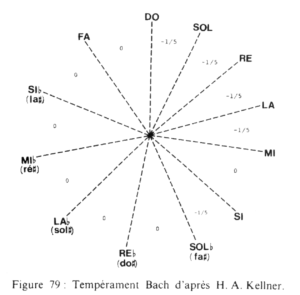
The BACH temperament designed by Johann Peter Kellner for the music of the 18th century (Asselin 2000 p. 101-103) contains two varieties of fifths (see tuning scheme). It is therefore not a "meantone" temperament.
It can be programmed in 3 steps:
- A series of descending fifths from "do-sol-re-la-mi", diminished by 1/5 comma;
- A series of ascending perfect fifths from "do" to "sol♭";
- An ascending perfect fifth from "mi" to "si".
The last interval is a remaining fifth "si-sol♭" ("B-G♭") diminished by exactly 1/5 comma (i.e. 697 cents).
The result is close to Werkmeister III (1691) (Asselin 2000 p. 94), with all positions close to the Pythagorean/harmonic series used for just intonation.
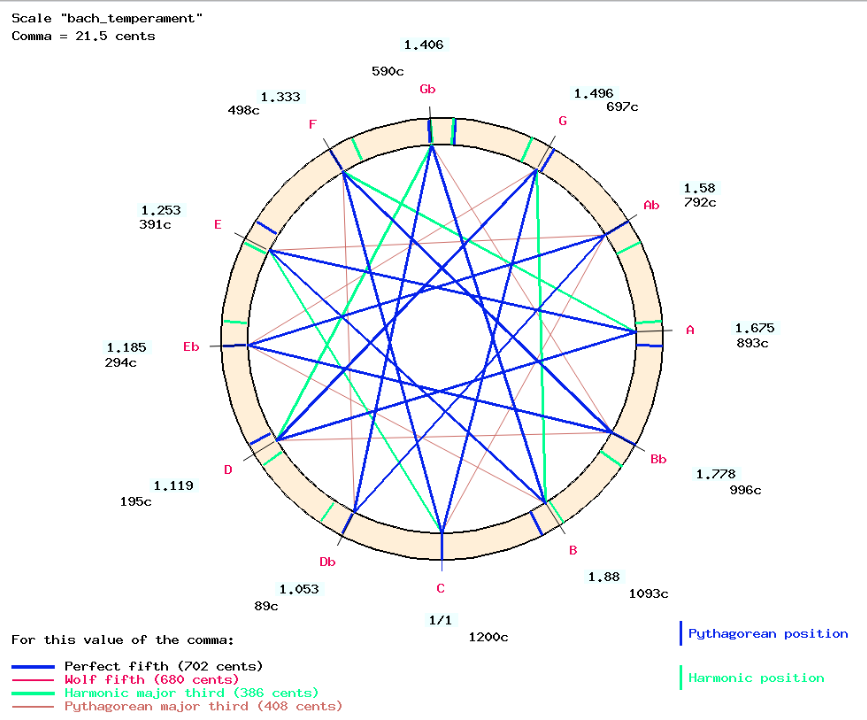
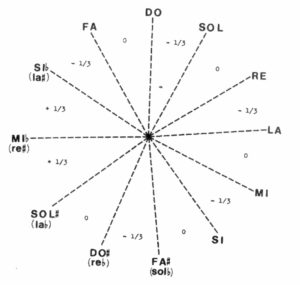
Source: Asselin (2000 p. 96)
The procedures for tuning temperaments with the Bol Processor sometimes differ from those used for physical instruments. Examples are Werckmeister IV (Asselin 2000 p. 96) and Werckmeister V (p. 99). To tune Werckmeister IV on an instrument (see picture), we start by tuning the sequence G C F Bb Eb Ab Db Gb B E as perfect descending fifths. Then interpolate three fifths (diminished by 1/3 comma) between G and E. Then retune G so that G D becomes a perfect fifth, which reduces C G by 1/3 comma. The same is done on E so that A E becomes a perfect fifth and E B is diminished by 1/3 comma. Similar adjustments are made to retune Bb, and finally Ab and Db to obtain the intervals shown on the picture.
On the Bol Processor the same procedure can be followed if the 1/3 comma correction is replaced by 7 cents. Another procedure is to "add" intervals, which is acceptable on a digital model because of the accuracy. This procedure is automatically summarised at the bottom of the "scale" page:
Werckmeister IV temperament (Asselin 2000 p. 96)
Added fifths down: “do,fa” starting fraction 1/1
Created meantone downward notes “fa,sib” fraction 3/2 adjusted -1/3 comma
Created meantone downward notes “sib,mib,sol#” fraction 3/2 adjusted 1/3 comma
Created meantone downward notes “sol#,do#” fraction 3/2
Created meantone downward notes “do#,fa#” fraction 3/2 adjusted -1/3 comma
Created meantone downward notes “fa#,si” fraction 3/2
Created meantone downward notes “si,mi” fraction 3/2 adjusted -1/3 comma
Created meantone downward notes “mi,la” fraction 3/2
Created meantone upward notes “do,sol” fraction 3/2 adjusted -1/3 comma
Created meantone upward notes “sol,re” fraction 3/2
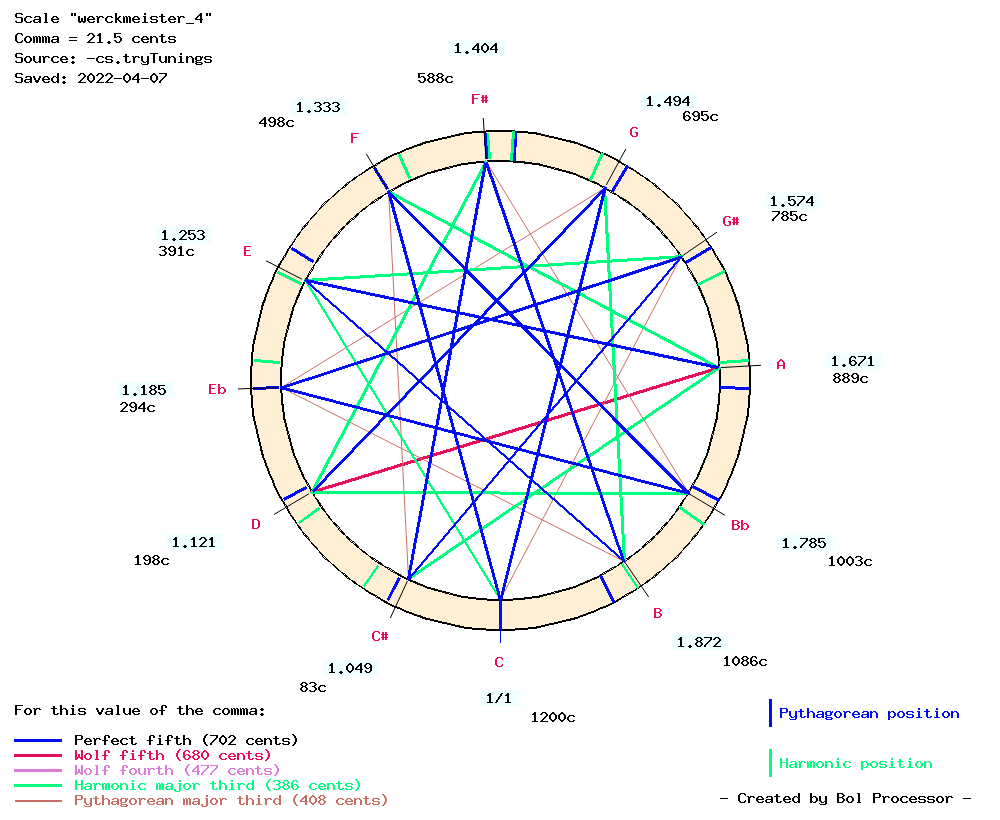
Let us compare some temperaments on ascending unaltered and descending altered scales…
Eighteen temperaments described by Pierre-Yves Asselin (2000) have been programmed in the "-to.trTunings" tonal resource. These can be checked against various musical works, see the pages Comparing temperaments and Tonal analysis of musical works.
As Schlick's temperament is not fully documented, we have set "do-la♭" as a pure major third and "mi-sol#" as a major third augmented by a 2/3 comma. As a result, "sol#" and "la♭" remain distinct.
Implementations of temperaments in the Bol Processor cannot be used as a reference because (1) errors may have occurred and (2) it is important to know the musical repertoire for which each temperament was designed. See also chapter VIII of Musique et tempéraments (Asselin 2000 p. 139-180) for the history of temperaments and musical examples discussed in terms of instrument tuning.
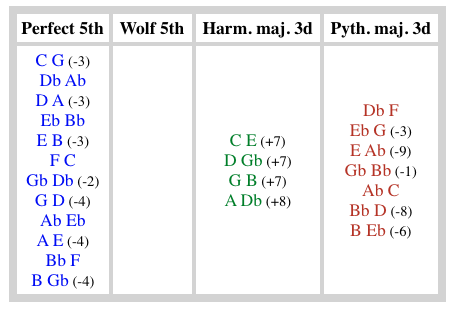
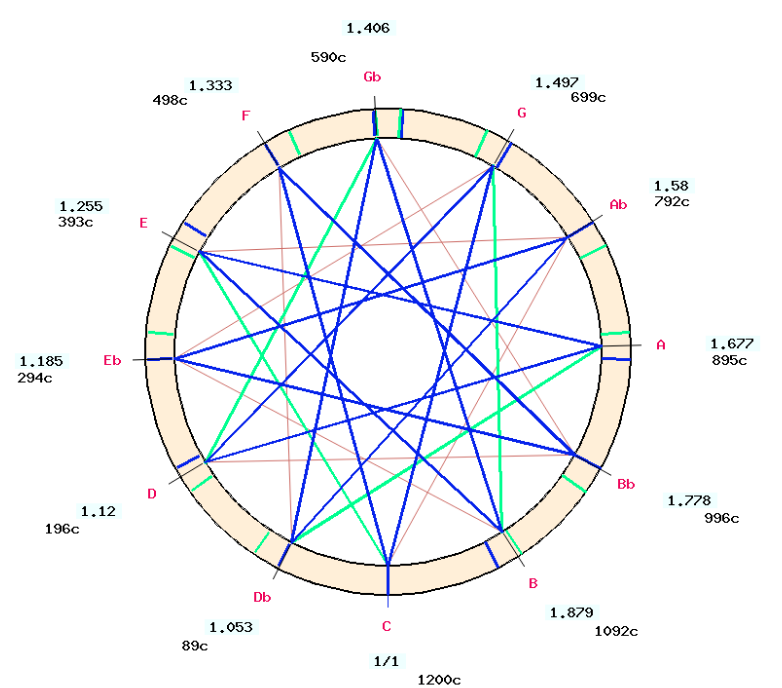
Circular graphs show noticeable intervals - perfect fifths, wolf fifths, harmonic and Pythagorean major thirds - in a wide range of uncertainty. For example, in the Tartini-Vallotti temperament shown above, "C-E" is listed as a harmonic major third (green segment), although it is slightly larger (+7 cents) than a "pure" major third (ratio 5/4). The safe way to check that this temperament matches its description is to read the deviations in the interval list (see picture).
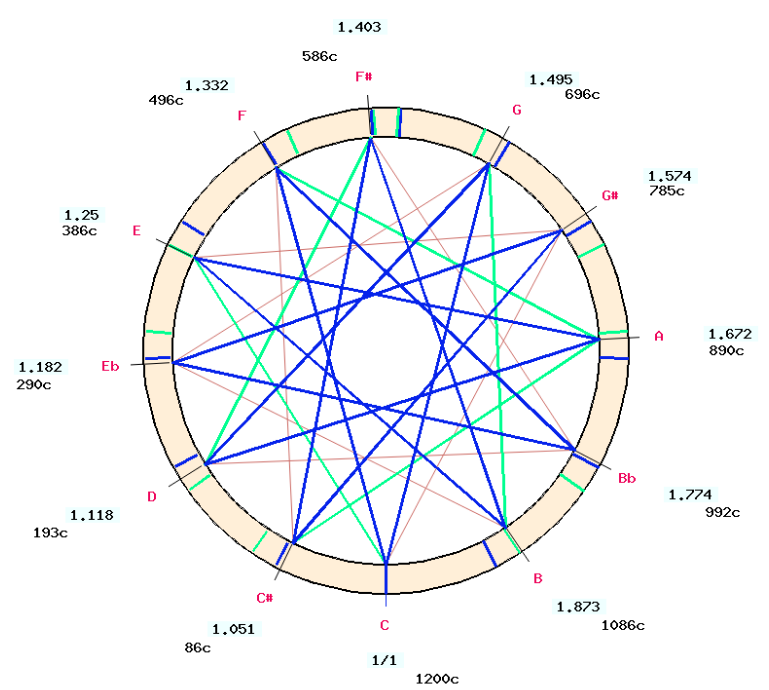
In a few temperaments the sizes of the fifths are not given explicitly, as the tuner is instructed to tune slightly larger (than perfect) or slightly smaller fifths. This is the case in the D'Alembert-Rousseau temperament (Asselin 2000 p. 119), where the series "do, fa, sib, mi♭, sol#" is expected to be slightly larger and "sol#, do#, fa#, si, mi" slightly smaller… In addition, the frame should be "complete", which implies the absence of a remaining comma fraction when closing the cycle of fifths.
In this example, the conditions were met by increasing the slightly larger fifths "do, fa, sib, mi♭, sol#" by 1/12 comma (+2 cents). To complete the cycle, the last series "sol#, do#, fa#, si, mi" was declared as equalised intervals. This resulted in the slightly smaller fifths being reduced by 2 cents to reflect the slightly larger ones. Incidentally, this -1/12 comma adjustment is also the one required to construct an equal-tempered scale.
The whole process of creating a scale is automatically recorded in the Comments section of the "scale" page, for example "d_alembert_rousseau":
D'Alembert-Rousseau temperament (Asselin 2000 p. 119)
Created meantone upward notes “do,sol,re,la,mi” fraction 3/2 adjusted -1/4 comma
Created meantone downward notes “do,fa,sib,mib,sol#” fraction 3/2 adjusted 1/12 comma
Equalized intervals over series “sol#,do#,fa#,si,mi” approx fraction 2/3 adjusted 2.2 cents to ratio = 0.668
It took us about 8 minutes to understand the procedure and another 8 minutes to tune the scale according to D'Alembert-Rousseau…
For a comparison of temperaments applied to several pieces of Baroque music, see the page Comparing temperaments.
The full set of tuning schemes currently implemented on the Bol Processor is presented on this page : https://bolprocessor.org/misc/figs/list-scales.php
More than 12 degrees
We will use a model from ancient Indian musicology to demonstrate divisions of more than 12 degrees per octave. This model is an interpretation of the description of the basic scales (grama) and their transpositions (murcchana) in Bharata Muni's Natya Shastra, a treatise dating from a period between 400 BCE and 200 CE — read the page The two-vina experiment.
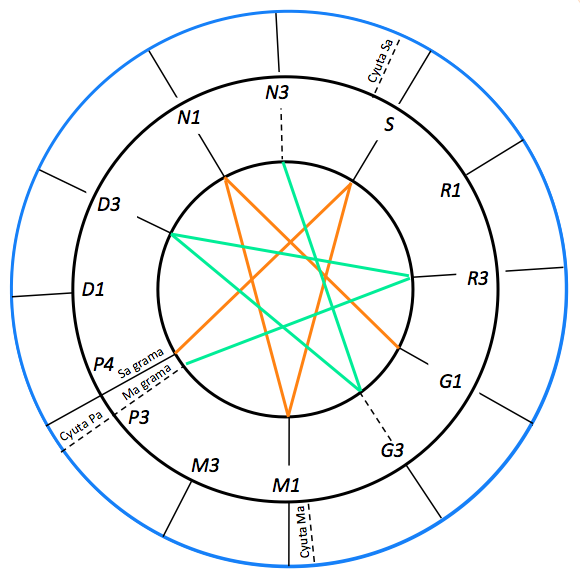
The grama-murcchana model and its application to Western harmony is described on the page Just intonation: a general framework. Its application to Hindustani music is presented on the page Raga intonation.
E.J. Arnold (1982) had designed a device to demonstrate the transposition of scales in Bharata's model. The actual division of the octave is 23 steps, but this amounts to having 22 optional positions (shruti-s) since the base note has only one option.
The result can be described as 11 pairs of note positions giving 211 = 2048 possible chromatic scales. Of these, only 12 are "optimally consonant", i.e. with only one "wrong" major fifth, short by 1 syntonic comma (pramāņa ṣruti), which here, for simplicity, is 21 cents.. These 12 chromatic scales are the ones that can be used in harmonic or modal music to experience the best consonance.
Below is a picture of the "grama" scale as displayed by the BP3 editor:
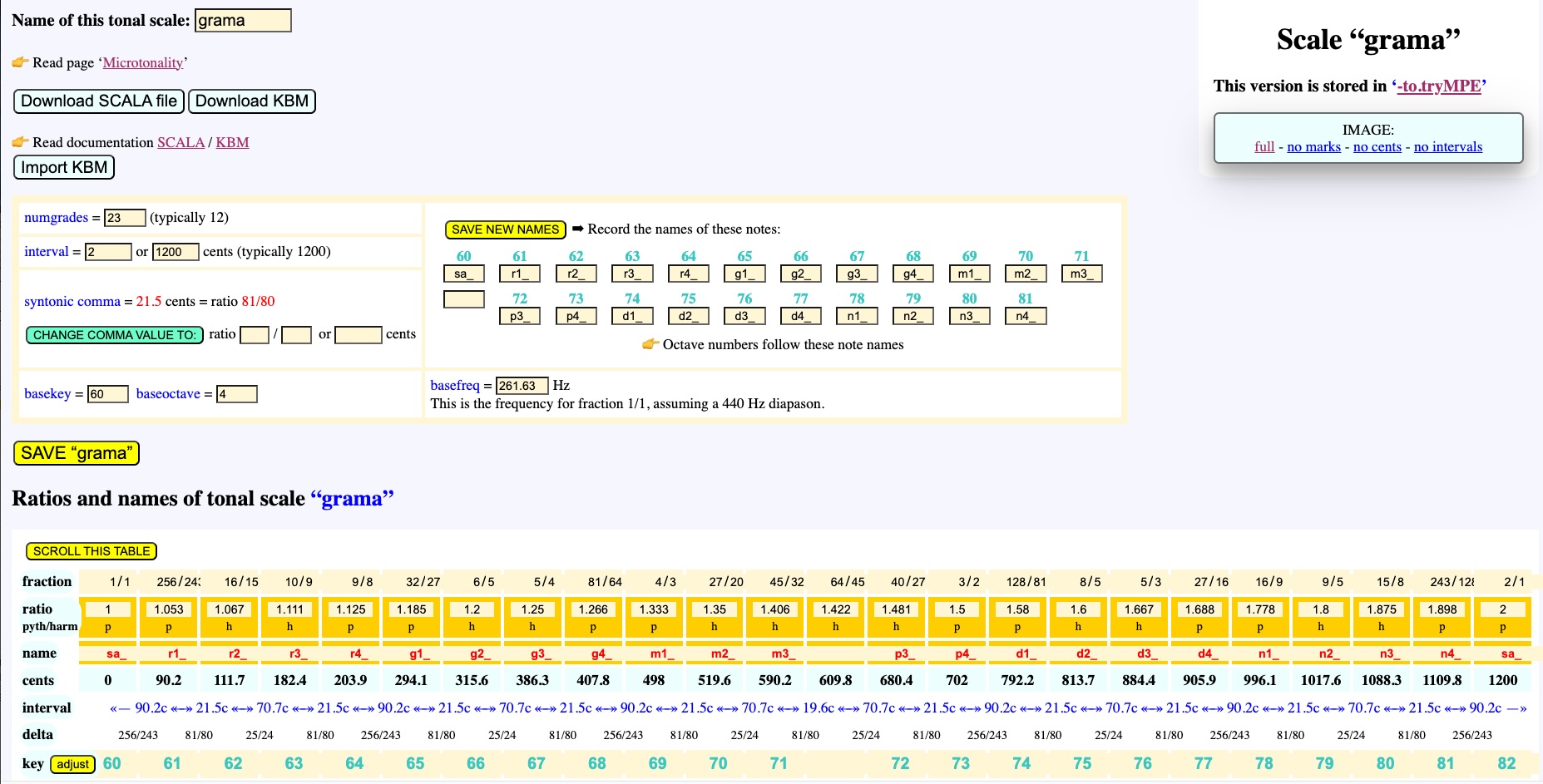
In this scale we use the conventional Indian sargam notation: sa, re, ga, ma , pa, dha, ni, translated as "C", "D", "E", "F", "G", "A", "B". Note that "re" ("D"), for example, can be found in four positions: r1 and r2 are the two possibilities for "D♭", the first one (256/243) being called "Pythagorean" (derived from five descending fifths) and the second one (16/15) "harmonic" (derived from one descending fifth and one descending major third). Positions r2 and r3 are "D♮" (natural) with r3 being harmonic (10/9) and r4 being Pythagorean (9/8).

(manufactured in Miraj)
There are special cases (visible on the wheel model) where m3 is almost superimposed on p1 and m4 with p2, their difference being an inaudible schisma (32805 / 32768 = 1.00112 = 1.9 cents). We use m3p1 and m4p2 to denote these merged positions.
The intervals given in cents are those identified by Western musicologists: the Pythagorean limma (256/243 = 90 cents), the syntonic comma (81/80 = 22 cents) and the minor semitone (25/24 = 70 cents). This shows that a shruti, as described by Bharata, can be of 3 different sizes. However, in its application to Indian music, this model should be rendered "flexible" with a size of the syntonic comma (pramāņa ṣruti) between 0 and 56.8 cents — see page The two-vina experiment.
Clicking on the IMAGE link displays a circular graphic representation of the "grama" scale:
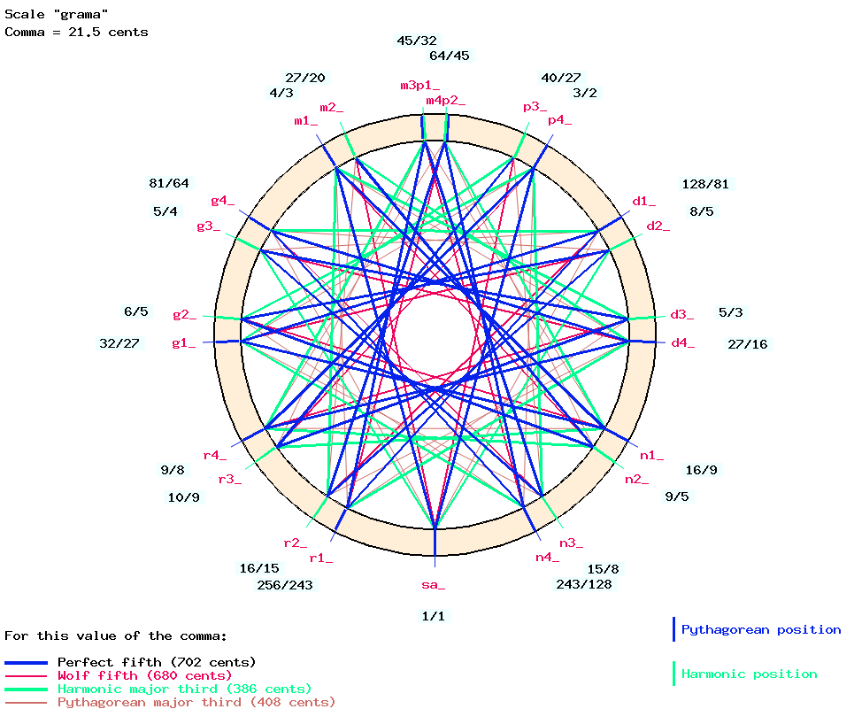
Let us play a diatonic scale according to the grama-murcchana model, an occurrence of Western just-intonation scales, and the piano stretched-octave tuning, again with "C4" (or "sa_4") as the block key. The grammar is called "-gr.tryShruti":
S --> _tempo(2) _scale(grama, sa_4) sa_4 r4_4 g3_4 m1_4 p4_4 d3_4 n3_4 sa_5 _scale(just intonation, C4) C4 D4 E4 F4 G4 A4 B4 C5 _scale(piano, C4) do4 re4 mi4 fa4 sol4 la4 si4 do5
The differences are barely perceptible for a simple reason: the first two are identical, since this just intonation scale is a special case of grama-murcchana, while the piano scale is a fair approximation of the former. This can be seen in the following Csound score:
Let us now listen to the 22 shrutis against a drone ("C" and "G" translated as sa and p4):
S --> scale(grama,sa_4) {9 Full_scale _ _ _ , Drone} - - tempo(3/4) {_retro Full_scale} _ _ _
Full_scale --> sa_4 r1_4 r2_4 r3_4 r4_4 g1_4 g2_4 g3_4 g4_4 m1_4 m2_4 m3p1_4 m4p2_4 p3_4 p4_4 d1_4 d2_4 d3_4 d4_4 n1_4 n2_4 n3_4 n4_4 sa_5
Drone --> _volume(30) Droneseq Droneseq Droneseq Droneseq Droneseq Droneseq Droneseq Droneseq
Droneseq --> {_legato(300) p4_3 sa_4 sa_4 sa_3}
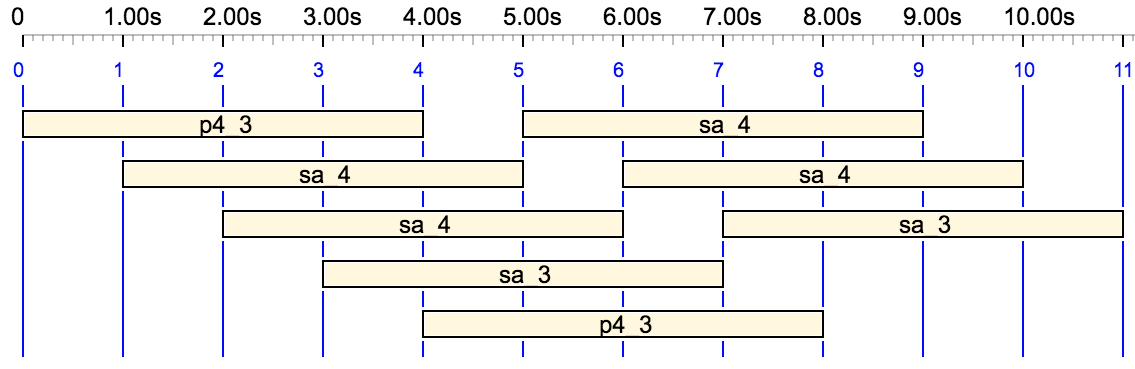
Note the use of the _retro performance tool to reverse the order of the Full_scale sequence. The _legato(300) command extends the duration of notes up to three times their current duration. This produces a Droneseq sound structure similar to that of the Indian tanpura.
In the sound rendering of this example, a 279 Hz sample waveform of a Miraj tanpura was used to feed the Karplus-Strong algorithm.
Listening to this sequence makes it clear that treating a sequence of shruti-s as a "scale" is iconoclastic for the aesthetics of Hindustani music: most of these notes sound out of tune when played in relation to a drone (the tanpura). As discussed on page The two-vina experiment, the presence of a drone makes it unlikely that mutual consonance in melodic intervals will always prevail over consonance with the drone's upper partials. If the grama-murcchana system has any relevance to the performance of classical ragas — see page Raga intonation — then at the very least the model should be made flexible enough to accommodate the correct intonation in melodic movements.
Comparing scales

A scale comparison tool is available on the tonal resource page. Click on COMPARE TONAL SCALES and select the ones that need to be analysed.
Scales are compared 2 by 2, so that a set of n scales gives n2/2 results, which are displayed in tables. The following is a comparison of scales called Amin, Cmaj and equal_tempered. The first two ones are described on the page Just intonation: a general framework.
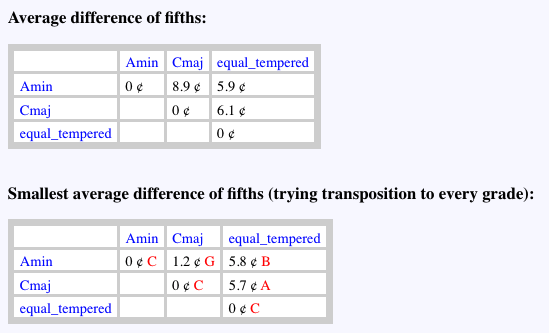
All comparisons are made on a 12-degree (chromatic) scale, measuring the sizes of perfect fifths — some of which may be wolf's fifths as explained on the just intonation page. The average difference of fifths is calculated by summing the squares of the differences between the sizes of fifths of identical degrees (counted in cents):
![]()
The distance between Amin and Cmaj is 8.9 cents and the distance between each of these scales and the equal-tempered one is almost 6 cents.
The second table is the result of a search for the smallest distance when transposing one of the scales by 1 to 11 semitones. Here we see that Amin (see picture) and Cmaj (see picture) are practically equivalent — they are harmonically related — since the difference goes down to 1.2 cents. The best matching version of Cmaj is constructed by transposing Amin up a fifth (7 semitones), thus moving 'C' to 'G'. For details of this procedure, see the section on Creation of just-intonation scales.
This device can be further developed to produce a classification of selected tonal scales highlighting similar/identical tuning schemes.
Another approach to tonal scale comparison is to assess the concordance between a musical work and the full set of documented tuning procedures: read the page Tonal analysis of musical works.
The syntactic model
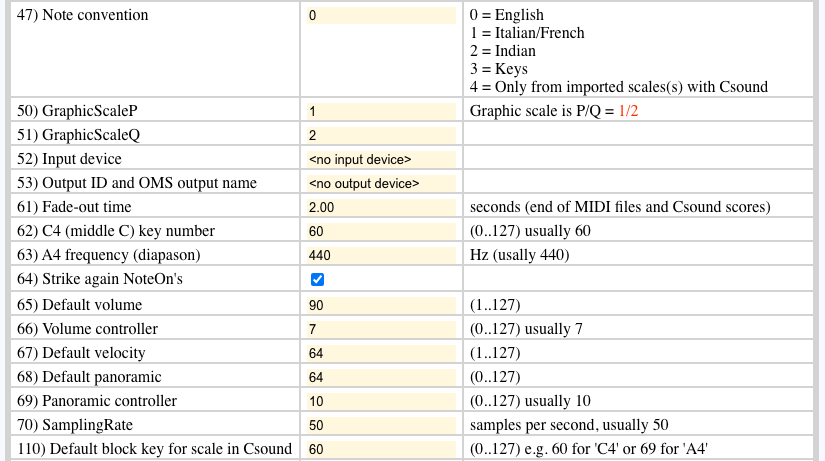
The following are guidelines for a correct and useful implementation of microtonal scales in BP3. We follow simple sequences listed in "-gr.tryOneScale". This grammar is linked to "-to.tryOneScale" which contains a unique just intonation scale with its notes labelled "Cj", "Cj#", "Dj" etc. In "-se.tryOneScale", the Note convention has been set to 0 (English), the 'C4' key number to 60 and the Default block key to 60. All these parameters are important to reproduce the same effects. Read the Check MIDI microtonality page for practical details.
Rule #1: If only 1 microtonal scale is loaded with the grammar, it will be used by default in all productions.
Example: Let us play:
S --> C4 A4 G4
It produces the following Csound score:
i1 0.000 1.000 261.630 90.000 90.000 0.000 0.000 0.000 0.000 ; Cj4
i1 1.000 1.000 436.137 90.000 90.000 0.000 0.000 0.000 0.000 ; Aj4
i1 2.000 1.000 392.445 90.000 90.000 0.000 0.000 0.000 0.000 ; Gj4
The display of "Cj4" etc. makes it clear that just intonation has been used. This is also confirmed by ratio 436.137/261.630 = 1.666 = 5/3.
Why not use the note labels "Cj4", "Aj"' and "Gj4" in the grammar? This only works if, for example, the scale is specified:
S --> _scale(just intonation, Cj4) Cj4 Aj4 Gj4
This will give the same Csound score because the block key "Cj4" is set to 261.630 Hz in the scale definition. Using "Aj4" as the block key would give:
S --> _scale(just intonation, Aj4) Cj4 Aj4 Gj4
and a sightly different Csound score:
i1 0.000 1.000 263.952 90.000 90.000 0.000 0.000 0.000 0.000 ; Cj4
i1 1.000 1.000 440.007 90.000 90.000 0.000 0.000 0.000 0.000 ; Aj4
i1 2.000 1.000 395.928 90.000 90.000 0.000 0.000 0.000 0.000 ; Gj4
Here, "Aj4" has been set to 440 Hz which is the diapason frequency in "-se.tryOneScale". The ratios are unchanged, e.g. 440.007/263.952 = 5/3.
How can we play equal-tempered intervals with this grammar? This is achieved by specifying the default scale: _scale(0,0):
S --> _scale(0,0) C4 A4 G4
yielding the following Csound score:
i1 0.000 1.000 8.00 90.000 90.000 0.000 0.000 0.000 0.000 ; C4
i1 1.000 1.000 8.09 90.000 90.000 0.000 0.000 0.000 0.000 ; A4
i1 2.000 1.000 8.07 90.000 90.000 0.000 0.000 0.000 0.000 ; G4
The frequencies are not explicit because the default Csound score format uses the octave point pitch-class representation, for example "A4" is the 9th pitch-class or the 8th octave (on a standard MIDI instrument). To make them explicit, just set the diapason in "-se.tryOneScale" to a slightly different value, for example 440.0001 Hz. This will produce:
i1 0.000 1.000 261.626 90.000 90.000 0.000 0.000 0.000 0.000 ; C4
i1 1.000 1.000 440.000 90.000 90.000 0.000 0.000 0.000 0.000 ; A4
i1 2.000 1.000 391.996 90.000 90.000 0.000 0.000 0.000 0.000 ; G4
We could expect the frequency of "C4" to be 261.630 Hz, but the value of 261.626 Hz differs due to rounding. The ratio of the difference is 261.630/261.626 = 1.000015 = 0.026 cents!
Rule #2: When parsing a sequence of notes, if a microtonal scale has been specified, the parser will first attempt to match the note against labels in the current microtonal scale. If there is no match, it will try to interpret the note according to the Note convention specified in settings.
For instance:
S --> _scale(just intonation, Cj4) Cj4 Aj4 Gj4 D4 F4 E4
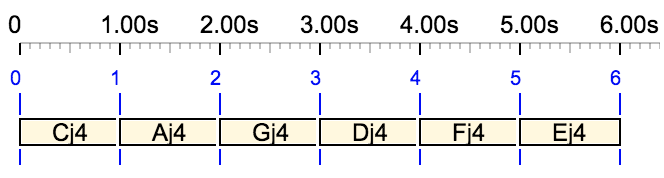
The notes in the sequence "D4 F4 E4" are translated to the corresponding positions in the intonation scale. The result is visible in both the Csound score and the graphic.
This practice is only relevant to 12-degree tonal scales where positions are equivalent — albeit with slightly different frequency ratios. For example, since the matching is based on key numbers, feeding the "grama" (23-degree) microtonal scale (see above) with "C4 D4 E4" would produce "sa_4 r2_4 r4_4", where r2_4 is close to "C#4" and r4_4 is close to "D4". This makes sense because the key sequence is 60-62-64. There is currently no generic way of mapping note positions in scales with different divisions. An additional difficulty would be scales with an interval other than 2/1.
We will show later that rule #2 provides a flexibility that makes it very easy to insert enharmonic corrections in a musical score by selecting one of 12 just-intonation chromatic scales — see the page Just intonation: a general framework.
Rule #3: If the parser cannot identify a note in the current microtonal scale and against the note convention, it will try other microtonal scales previously loaded in the sequence.

This can be demonstrated with "-gr.tryScales". At the top of the grammar are listed the scales that will be sent to the console along with the grammar and instructions. Each scale becomes "active" in the grammar once a _scale() operator has declared it.
Let us try to produce:
S --> _scale(piano,dop4) fap3 _scale(just intonation,69) C4 rep4
Active scales are piano, then just intonation. There are no problems with note "fap3", which belongs to the piano scale, nor with "C4" which is known in the English note convention. As predicted by rule #2, the note "C4" is translated to its equivalent "Cj4" and played in just intonation.
Since the baseoctave of the scale piano is 3 (see the image above), the pitch of "fap3" will be close to that of "F4".
What happens to note "rep4"? If the piano scale had not been activated, this note would be rejected as a syntax error. However, following rule #3, the parser finds it in the piano scale. This results in the key number 74 since baseoctave = 3.
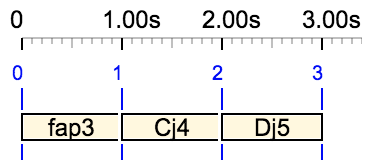
The note is interpreted as key #74 in the just intonation scale, displayed as "Dj5". This can be seen in the Csound score below and in the graphic.
i1 0.000 1.000 349.538 90.000 90.000 0.000 0.000 0.000 0.000 ; fap3
i1 1.000 1.000 263.952 90.000 90.000 0.000 0.000 0.000 0.000 ; Cj4
i1 2.000 1.000 593.891 90.000 90.000 0.000 0.000 0.000 0.000 ; Dj5
As a result, notes found in a sequence are always interpreted as belonging to the scale declared immediately to the left, even if their label belongs to a different scale or note convention.
Therefore, it is not a good idea to mix notes belonging to different scales without declaring the scale before they occur. A "_scale()" declaration is best placed at the beginning of each sequence, especially at the beginning of the right argument of a rule.
References
Arnold, E.J. A Mathematical model of the Shruti-Swara-Grama-Murcchana-Jati System. Journal of the Sangit Natak Akademi, New Delhi 1982.
Asselin, P.-Y. Musique et tempérament. Paris, 1985, republished in 2000: Jobert. Soon available in English.