Microtonality

Microtonality is a top­ic addressed by many musi­cal sys­tems that deal with tonal inter­vals: the use of micro­tones — inter­vals small­er than a semi­tone, also called “microin­t­er­vals”. It can also be extend­ed to include any music that uses inter­vals not found in the com­mon west­ern tun­ing of twelve equal inter­vals per octave. In oth­er words, a micro­tone can be thought of as a note that falls between the keys of a piano tuned to equal tem­pera­ment (Wikipedia).

All exam­ples shown on this page are avail­able in the sam­ple set bp3-ctests-main.zip, which is shared via GitHub. Follow the instruc­tions on page Bol Processor ‘BP3’ and its PHP inter­face to install BP3 and learn its basic oper­a­tion. Download and install Csound from its dis­tri­b­u­tion page.

A brief presentation

On elec­tron­ic instru­ments such as the Bol Processor asso­ci­at­ed with Csound, micro­tonal­i­ty is a mat­ter of “micro­ton­al tun­ing”, here mean­ing the con­struc­tion of musi­cal scales alien to the con­ven­tion­al one(s).

Equal tem­pera­ment is an intu­itive mod­el that divides the octave (fre­quen­cy ratio 2/1) into 12 “equal” inter­vals called semi­tones. Each semi­tone has a fre­quen­cy ratio of 2 ^1/12 = 1.059. Tonal inter­vals are gen­er­al­ly expressed on a log­a­rith­mic scale, which gives the ratio 2/1 a val­ue of 1200 cents. Each semi­tone is there­fore worth 100 cents in a con­ven­tion­al scale system.

An equal tem­pered scale is use­ful for mak­ing a piece of music sound the same when trans­posed to anoth­er key. However, its inter­vals do not cor­re­spond to the (pre­sum­ably) “nat­ur­al” inter­vals con­struct­ed from whole-number fre­quen­cy ratios using the num­bers 3, 4, 5. These sim­ple ratios give the impres­sion of con­so­nance because the fre­quen­cies of the upper par­tials (har­mon­ics) can coin­cide: if two strings vibrate at a fre­quen­cy ratio of 3/2 (a “per­fect fifth”), the 3^rd har­mon­ic of the low­est vibra­tion is at the same fre­quen­cy as the 2^nd har­mon­ic of the high­er vibration.

In an equal tem­pered scale, the har­mon­ic major third (C-E) of 400 cents has a ratio of 1.26 instead of 1.25 (5/4). The major fifth (C - G) also sounds slight­ly “out of tune” with a ratio of 1.498 instead of 1.5 (3/2). These mis­match­es can pro­duce beats that are con­sid­ered unpleas­ant in har­mon­ic contexts.

When tun­ing stringed instru­ments (such as the piano), octaves can be stretched a lit­tle to com­pen­sate for a slight inhar­monic­i­ty of the upper par­tials pro­duced by vibrat­ing strings (in high­er octaves), as advo­cat­ed by Serge Cordier. A val­ue of 1204 cents sounds fair, with the added advan­tage of mak­ing fifths sound “per­fect” in a 3/2 ratio. With this set­ting, the fre­quen­cy ratio of the stretched octaves is 2^(1204/1200) = 2.0046. This effect can be repro­duced in elec­tron­ic instru­ments such as dig­i­tal pianos that imi­tate mechan­i­cal ones. We will see how it can be imple­ment­ed in the Bol Processor BP3 + Csound.

Musicologists agree that equal tem­pera­ment was nev­er exact­ly achieved on clas­si­cal instru­ments such as pipe organs and harp­si­chords. Rather, instru­ment tuners have devel­oped rules for repro­duc­ing the most pleas­ing inter­vals in par­tic­u­lar musi­cal con­texts. In oth­er words, a mechan­i­cal instru­ment should be tuned accord­ing to a style and reper­toire of music. Pierre-Yves Asselin (2000) has pub­lished a detailed com­pi­la­tion of tun­ing tech­niques used by European musi­cians and instru­ment mak­ers over the past cen­turies — lis­ten to exam­ples on the page Comparing tem­pera­ments. The same flex­i­bil­i­ty can be achieved with sounds pro­duced by “algo­rithms”.

Outside of west­ern clas­si­cal music, a wide vari­ety of tonal sys­tems delib­er­ate­ly reject 12-tone-in-one-octave tonal­i­ty. Arabic-Andalusian music is often described as a “quar­ter­tone” sys­tem, which divides the octave into 24 inter­vals. Equal tem­pered scales of 7 degrees have been iden­ti­fied on var­i­ous tra­di­tion­al African instru­ments. The grama-murcchana the­o­ret­i­cal mod­el of tonal music in India claims the use of 22 shru­ti-s, pre­sum­ably microin­t­er­vals of unequal size (see below).

The scale() operator in Bol Processor BP3 + Csound

Csound scores are flex­i­ble in the way they rep­re­sent tonal posi­tions. A com­mon con­ven­tion is the octave point pitch class. For exam­ple, the note “A4” would be assigned the tonal posi­tion “8.09”, mean­ing that it is the 9^th note in the 8^th octave (in the English con­ven­tion). This val­ue pro­duces a note at the dia­pa­son fre­quen­cy (usu­al­ly 440 Hz) on a Csound instrument.

It is also pos­si­ble to spec­i­fy the note posi­tion by its fre­quen­cy in cycles per sec­ond (cps mode). This allows a high lev­el of accu­ra­cy as fre­quen­cies are expressed in float­ing point. For exam­ple, in this for­mat, “A4” would be assigned “440.0”. Accuracy bet­ter than 1‰ is not noticeable.

As explained on page Csound tun­ing in BP3, it is pos­si­ble to send notes in both the octave point pitch class and cps for­mats to the same Csound instru­ment. In fact, micro­ton­al scales will only use cps. The cps mode is also used by BP3 when­ev­er the dia­pa­son fre­quen­cy is not exact­ly 440 Hz. To make all fre­quen­cies vis­i­ble on Csound scores, for exam­ple, set the dia­pa­son to “400.01”…

Let us take a sim­ple exam­ple to demon­strate the use of mul­ti­ple scales. The gram­mar is:

-se.tryScales
-cs.tryScales
ORD
S --> _scale(0,0) C4 E4 A4 {8,{C4,E4,G4,C5}} {8,{C4,Eb4,G4,C5}} - _scale(piano,C4) C4 E4 A4 {8,{C4,E4,G4,C5}}{8,{C4,Eb4,G4,C5}} - _scale(just into­na­tion,C4) C4 E4 A4 {8,{C4,E4,G4,C5}} {8,{C4,Eb4,G4,C5}}

In this gram­mar, the same sequence is repeat­ed three times in dif­fer­ent tunings:

• _scale(0,0) is the default tun­ing = 12-degree equal-tempered
• _scale(piano, C4) refers to the “piano” scale
• _scale(just into­na­tion, C4) refers to a (so-called) “just-intonation” scale

Note “C4” appear­ing in these oper­a­tors is the block key, here mean­ing the key that must cor­re­spond to its equal tem­pera­ment val­ue in the tun­ing set by the scale.

It may be nec­es­sary to lis­ten sev­er­al times to notice sub­tle differences:

The sound is pro­duced by the Csound instru­ment “new-vina.orc” designed by Srikumar Karaikudi Subramanian to imi­tate the Sarasvati vina, a long-stringed instru­ment played in South India — lis­ten to his demo: Sarasvati vina. This type of instru­ment is capa­ble of high­light­ing the finest tonal subtleties.

Beats are audi­ble in the equal-tempered ver­sion, but slight­ly less so in the piano ver­sion, and almost absent in the just-intonation ren­der­ing. Looking at the Csound score makes it easy to check the­o­ret­i­cal models:

Show Csound score

In the Csound score, note names have been auto­mat­i­cal­ly replaced with their trans­la­tions in the def­i­n­i­tions of scales piano and just into­na­tion (see below). For exam­ple, in the piano scale of this exam­ple, ‘C4’, ‘D4’, ‘E4’… have been replaced by ‘do3’, ‘re3’, ‘mi3’ with an addi­tion­al ‘p’ mark­er: ‘dop3’, ‘rep3’, ‘mip3’… In the same way, just into­na­tion notes are labelled ‘Cj4’, ‘Dj4’, ‘Ej4’ etc. This renam­ing is option­al since all these scales are made up of 12 degrees with iden­ti­cal key posi­tions, but it is used here to make the Csound score more explicit.

The use of “C4” as a block key means that it is always played at a fre­quen­cy of 261.630 Hz. Consequently, “A4” is at 440 Hz in the first occur­rence and a lit­tle high­er in the piano ver­sion due to the octave stretch­ing with a ratio of 524.463 / 261.630 = 2.0046, which is 1204 cents.

Finally, we notice that, as pre­dict­ed by the mod­el, the per­fect major fifth (C - G) pro­duces the same posi­tions (392.445 Hz) in the piano and just into­na­tion scales.

➡ In real­i­ty, the “just into­na­tion” frag­ment in this exam­ple would be out of tune if we fol­low the frame­work of tonal­i­ty pro­posed by Asselin (2000) and con­firmed by an exten­sion of the ancient grama-murcchana sys­tem in India. In the last “C minor” chord {C4,Eb4,G4,C5}, the notes “C4”, “C5” and “G4” should be low­ered by a syn­ton­ic com­ma. This means that play­ing “just into­na­tion” in west­ern har­mo­ny requires more than a sin­gle just-intonation scale: each har­mon­ic con­text requires its own spe­cif­ic tun­ing, which indeed can­not be achieved on key­board instru­ments. A method for con­struct­ing just-intonation scales and using them in Bol Processor music is giv­en on the page Just into­na­tion: a gen­er­al frame­work.

Looking at two scales

From the gram­mar page “-gr.tryScales” we can fol­low the Csound resource file “-cs.tryScales” which con­tains scale and instru­ment def­i­n­i­tions. The same file con­tains instruction

f1 0 256 1 “vina-wave-table.aiff” 0 4 0

telling the Csound instru­ment to use the “vina” waveform.

The fol­low­ing is a rep­re­sen­ta­tion of the piano scale (Cordier’s equal temperament):

All the inter­vals were set in a sin­gle click, after enter­ing “1204” as the size of the octave in cents, which set the last ratio to 2.004 (approx­i­mate­ly 501/250). The “INTERPOLATE” but­ton was then clicked to cal­cu­late the inter­me­di­ate ratios.

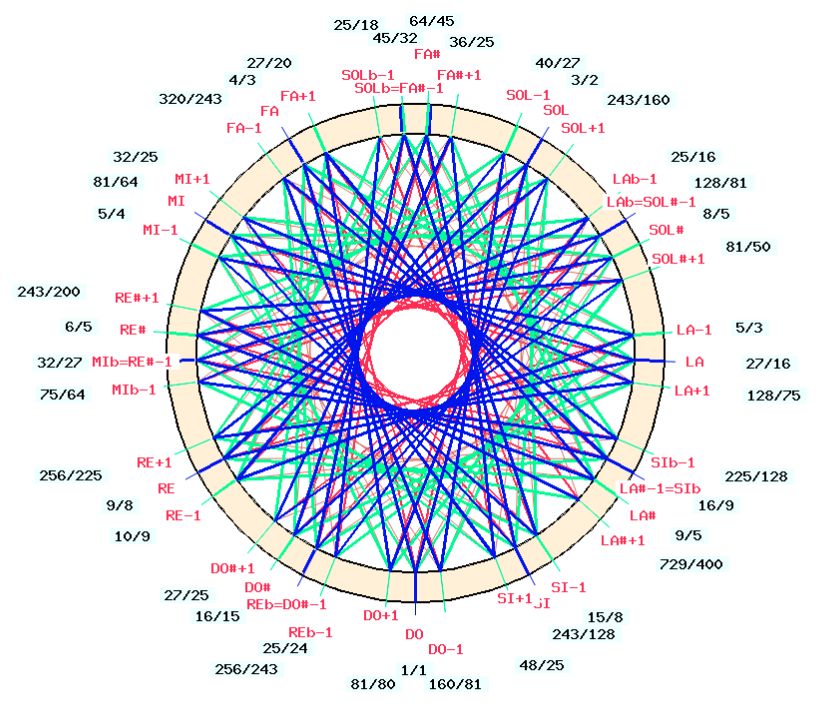
The scale is dis­played as a cir­cu­lar graph by click­ing on the “IMAGE” link:

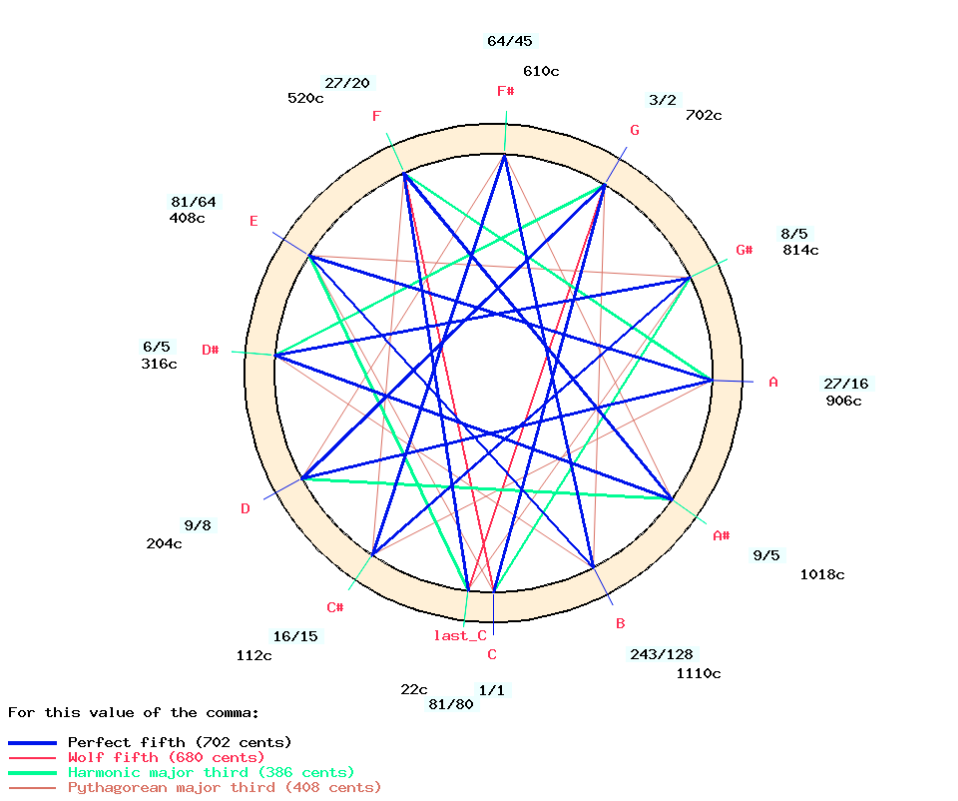
The dis­play con­firms that the posi­tion of “G” (“solp”) is in the ratio 3/2 or 702 cents. However, the tonal dis­tance between “G” (“solp”) and “D” (“rep”) is slight­ly small­er (699 cents), which means that this scale is not a pure cycle of fifths, as the lat­ter would have end­ed after 12 steps with an octave extend­ed by a Pythagorean com­ma (scale “twelve_fifths” in “-cs.tryScales”):

The basekey is the key used to pro­duce base­freq. Here base­freq is set to 261.630 Hz for key #60 which is usu­al­ly the “mid­dle C” on a piano key­board. The base­freq para­me­ter has an effect on the pitch which is fur­ther adjust­ed by the val­ue of the dia­pa­son entered in “-se.tryScales”. If the dia­pa­son is set to 430 Hz, the fre­quen­cy of “C4” would be 261.630 x 430 / 440 = 255.68 Hz.

The baseoc­tave para­me­ter is not stored in the Csound func­tion table, but is required by the Bol Processor to name notes cor­rect­ly. This scale uses the Italian/French note con­ven­tion, where key #60 is called “do3” instead of “C4”. Therefore baseoc­tave = 3.

Temperament

At the bot­tom of the “Scale” page is a form for con­struct­ing scales in musi­cal tem­pera­ment. The scope of this pro­ce­dure is wider than usu­al because the inter­face per­mits the mod­i­fi­ca­tion of any series of inter­vals, not just fifths and fourths.

Bol Processor pro­ce­dures for the pro­duc­tion of tem­pered scales (and all scales in gen­er­al) can be used both to visualise/hear inter­vals and chords derived from a the­o­ret­i­cal descrip­tion of the scale, and to check that a pro­ce­dure for tun­ing a mechan­i­cal instru­ment con­forms to its the­o­ret­i­cal descrip­tion. Below is an exam­ple of both approach­es applied to Zarlino’s mean­tone tem­pera­ment (tem­péra­ment méso­tonique).

The long his­to­ry of the tem­pera­ment in European music is cov­ered in Pierre-Yves Asselin’s dis­ser­ta­tion and pub­li­ca­tion (2000, p. 139-150). During the 16^th and 17^th cen­turies, European musi­cians tend­ed to pre­fer “pure” major thirds (fre­quen­cy ratio 5/4) at the cost of com­pro­mis­ing the size of the fifths. This was called the “pure third mean­tone tem­pera­ment” (tem­péra­ment méso­tonique à tierces majeures pures) which was gen­er­al­ly achieved by reduc­ing the size of cer­tain fifths by a frac­tion of the syn­ton­ic com­ma (Asselin 2000 p. 76). After this peri­od, there was anoth­er fash­ion of using per­fect fifths (fre­quen­cy ratio 3/2) and com­pro­mis­ing the size of major thirds in the same way. Both meth­ods — and many more — are imple­ment­ed in the Bol Processor inter­face. Algorithmic tun­ing is indeed eas­i­er to achieve than tun­ing a mechan­i­cal instrument!

Zarlino, theory

Let us try Zarlino’s mean­tone tem­pera­ment (Asselin 2000 p. 85-87) which was pop­u­lar in the 16^th and 17^th cen­turies. It con­sists of 12 fifths start­ing from “E♭” (“mi♭”) up to “G#” (“sol#”) dimin­ished by 2/7 of a syn­ton­ic com­ma — that is 6 cents.

➡ This should not be con­fused with Zarlino’s “nat­ur­al scale” which is an instance of just into­na­tion.

Theoretically, this takes two steps from the pre­vi­ous­ly known posi­tion “C”.

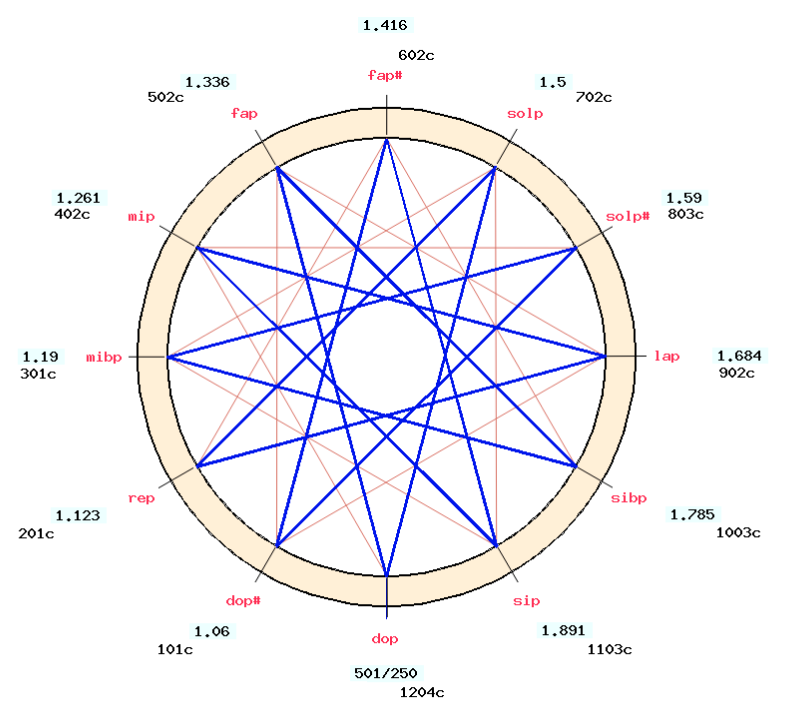
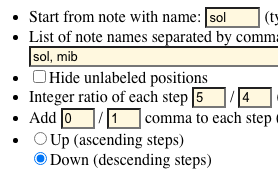
First we enter the start­ing note “do” and the sequence of fifths “do, sol, re…, sol#”, spec­i­fy­ing ratios equal to 3/2 with a mod­i­fi­ca­tion of -2/7 com­ma (see picture).

Then we do the same with fourths (descend­ing fifths) start­ing from “do” (“C”) down to “mi♭” (“E♭”).

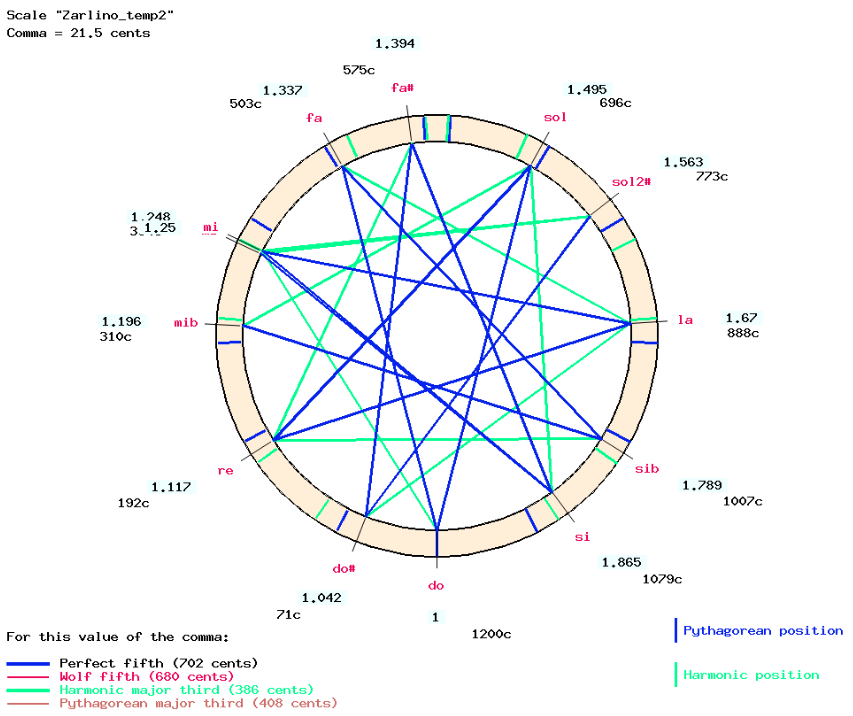
The result is dis­played by click­ing on the IMAGE link:

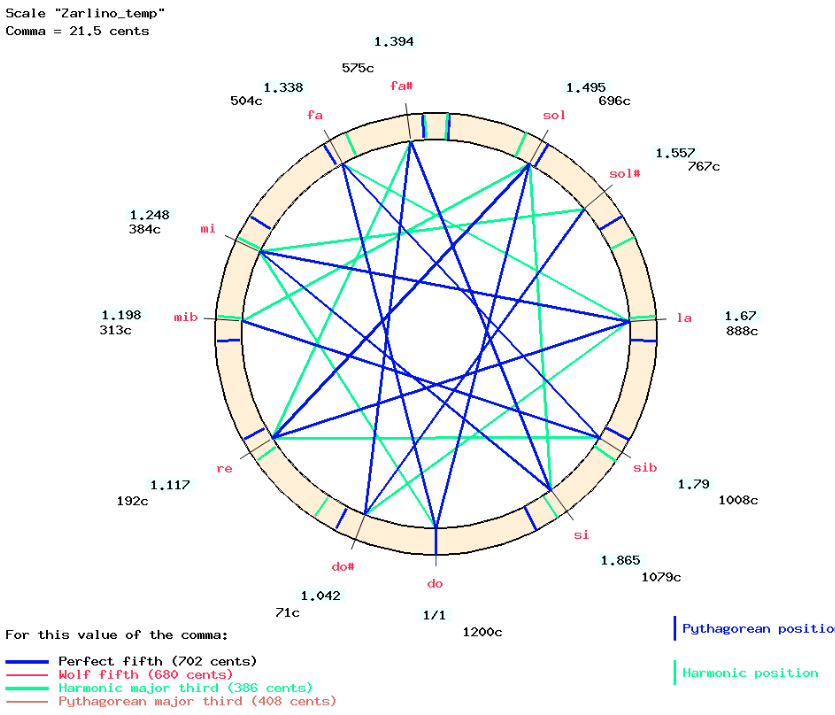
In this tem­pera­ment, the har­mon­ic major thirds (green con­nec­tions on the graph) are equal and slight­ly small­er (384 cents) than the “pure” ones (ratio 5/4 or 386 cents). Semitones between unal­tered and altered notes are equal (71 cents). All major tones are equal (192 cents) except “do#-mi♭” and “sol#-sib” (242 cents).

Noticeable dis­so­nances are found in the “sol#-mi♭” fifth (746 cents, i.e. an extra 2 + 1/7 com­mas = 44 cents) and major thirds such as “sol#-do”, “do#-fa”, “fa#-sib” and “si-mi♭” which are larg­er (433 cents) than Pythagorean major thirds (408 cents). Obviously, these inter­vals are not intend­ed to be used in the musi­cal reper­toire to which this tun­ing is applied…

Comparison

A layper­son might won­der whether small tonal adjust­ments — often less than a quar­ter of a semi­tone (i.e. 25 cents) — have any notice­able effect on musi­cal works using these tun­ing sys­tems. Comparative exper­i­ments are easy with the Bol Processor.

For exam­ple, let us play one (of a bil­lion vari­a­tions) of Mozart’s musi­cal dice game, with tun­ing options select­ed by acti­vat­ing a first rule in “-gr.Mozart”:

// gram#1[1] S --> _vel(80)_tempo(3/4) _scale(0,0) A B // Equal tem­pera­ment
// gram#1[2] S --> _vel(80) _tempo(3/4) _scale(piano,0) A B // Equal tem­pera­ment (Cordier)
// gram#1[3] S --> _vel(80) _tempo(3/4) _scale(Zarlino_temp,0) A B // Zarlino’s tem­pera­ment
// gram#1[4] S --> _vel(80) _tempo(3/4) Ajust Bjust // Just intonation

Musical pro­duc­tions are list­ed below. The ran­dom seed has been set to 998 (in “-se.Mozart”) as this vari­a­tion con­tains a greater num­ber of chords, and the per­for­mance has been slowed down by “_tempo(3/4)”.

It is impor­tant to remem­ber that of these options, only the first three ones (tem­pera­ments) are acces­si­ble on fixed-pitch instru­ments with 12-degree key­boards. The last one (just into­na­tion) requires a “retun­ing” of each har­mon­ic con­tent — see page Just into­na­tion: a gen­er­al frame­work.

The first option (equal tem­pera­ment) is the default tun­ing of most elec­tron­ic instruments:

The sec­ond option is an equal tem­pera­ment with octaves stretched by 4 cents, as advo­cat­ed by Serge Cordier (see above):

The third option is Zarlino’s temperament:

The last option is “just intonation”:

Zarlino: a simulation of physical tuning

The tun­ing of mechan­i­cal instru­ments (such as a harp­si­chords) requires dif­fer­ent pro­ce­dures from the pro­gram­ming of “tem­pered” scales on the Bol proces­sor. However, by using the com­put­er, it is pos­si­ble to quick­ly ver­i­fy that the mechan­i­cal pro­ce­dure would pro­duce the expect­ed result. Let us demon­strate this using Zarlino’s temperament.

On the com­put­er we had pro­grammed a series of 7 ascend­ing fifths dimin­ished by a 2/7 com­ma from “do” to “do#”. This is impos­si­ble to achieve “by ear” on a mechan­i­cal instru­ment. Pierre-Yves Asselin (2000 p. 86) revealed the method shown below.

First step

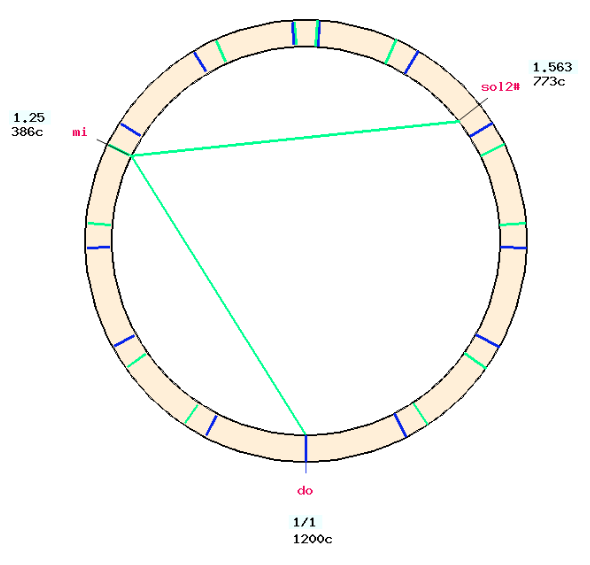
From “do”, tune two suc­ces­sive major thirds. This results in a “sol#” which is posi­tioned at a fre­quen­cy ratio of 25/16 (773 cents) above “do”.

This “sol#” is actu­al­ly “SOL#+2” of the 2^nd order har­mon­ic fifths down series in Asselin’s tun­ing frame­work (2000 p. 62) — see page Just into­na­tion: a gen­er­al frame­work. It is not exact­ly the one expect­ed on Zarlino’s mean­tone tem­pera­ment, although it is close. It is labelled “sol2#”.

Second step

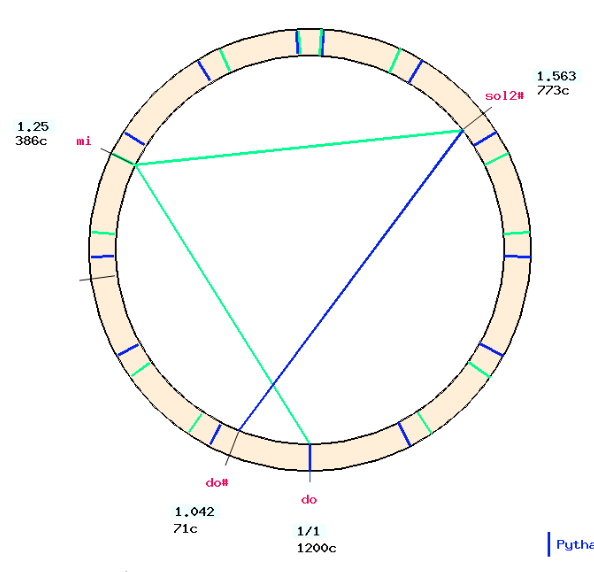
From “sol2#” tune down a per­fect fifth, result­ing in “do#”.

Be care­ful to pro­gram a per­fect fifth, which is spec­i­fied on the form as “add 0/1 com­ma”. There is also a form for cre­at­ing series of per­fect fifths which can be used for this step.

The result­ing “do#” (ratio 1.04166) is exact­ly 5²/3/2³, as expect­ed in Zarlino’s mean­tone tem­pera­ment (Asselin 2000 p. 194).

Third step

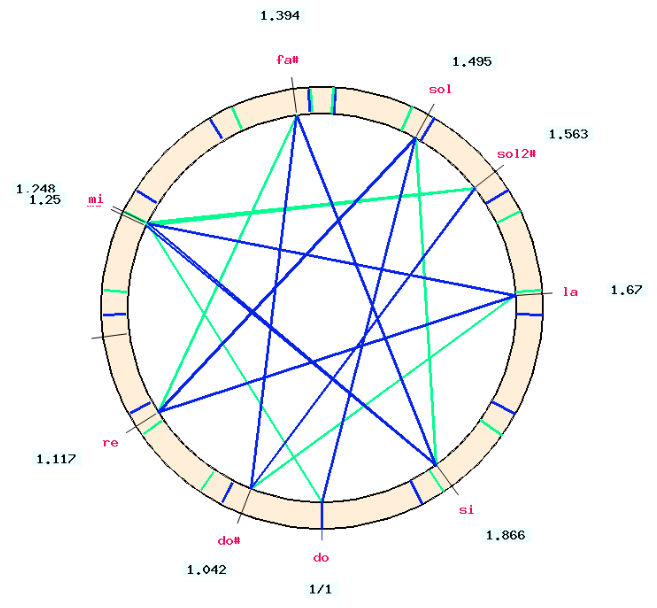
Tune 7 equal fifths between “do” and “do#”. Equalising fifths is a typ­i­cal pro­ce­dure for tun­ing mechan­i­cal instru­ments. The Bol Processor has a gen­er­al pro­ce­dure for equal­is­ing inter­vals over a series of notes. Here we spec­i­fy that these inter­vals should be close to the frac­tion 3/2, even though we know that they will end up as fifths dimin­ished by a 2/7 comma.

The miss­ing notes “sol, re ‚la, si, fa#” are cre­at­ed. For the exist­ing note “mi”, the machine checks that its cur­rent posi­tion is close to the one pre­dict­ed by the approx­i­mate fraction.

The graph shows that the cal­cu­lat­ed posi­tion of “mi” (ratio 1.248) is slight­ly dif­fer­ent from its pre­vi­ous posi­tion (1.25), but this dif­fer­ence is neg­li­gi­ble. We keep both posi­tions on the graph, know­ing that only one will occur in a phys­i­cal tuning.

Fourth step

Now tune down 3 fifths from “do” to “mi♭”, dimin­ished by a 2/7 com­ma. This can be done by repro­duc­ing “by ear” inter­vals cre­at­ed in the pre­vi­ous step. Another method is to tune “mi♭” a har­mon­ic major third below “sol” as shown on the form.

Fifth step

Once “mi♭” has been tuned we can tune three equal fifths (in fact dimin­ished by 2/7 com­ma) between “mi♭” and “do”. Again we use the “equal­ize inter­vals” pro­ce­dure. At this stage, the posi­tions of “si♭” and “fa” are created.

The result is shown in the graph below:

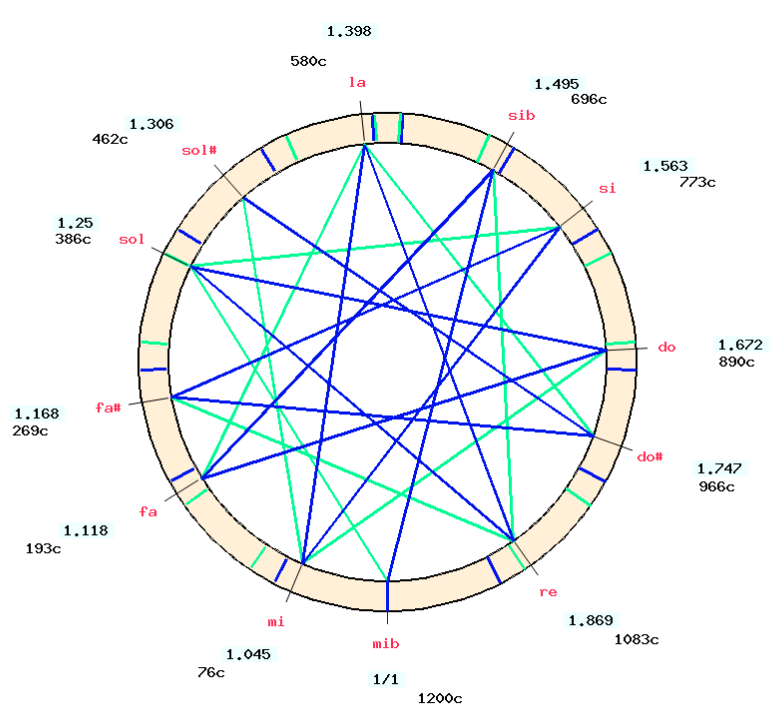
On this graph, the ratio 1.563 for “sol#” is close (with­in 7 cents) to 1.557 of Zarlino’s tem­pera­ment. On a mechan­i­cal instru­ment, since “mi” tuned by equal­is­ing fifths (3^d step) was at posi­tion 1.248, adjust­ing the “mi-sol#” major third to a 5/4 ratio would set “sol#” at a bet­ter ratio (1.56).

More temperaments

All the tem­pera­ments list­ed in Asselin’s the­sis can be eas­i­ly pro­grammed on the Bol Processor. Take, for exam­ple, a clas­si­cal mean­tone tun­ing (Asselin 2000 p. 76), pop­u­lar in the 16^th and 17^th cen­turies, also known as Chaumont (Asselin 2000 p. 109) . Its aim is to pro­duce “pure thirds” (ratio 5/4). It con­sists of a series of fifths from “mi♭” (“E♭”) to “sol#” (“G#”) dimin­ished by a 1/4 com­ma. The prob­lem is that the tun­ing scheme — unlike Zarlino’s mean­tone — does not start from “do” (“C”). There are two solutions.

The first solu­tion is to divide the series of fifths into two parts: first cre­ate the series “do, sol, re, la, mi, si, fa#, do#, sol#” of ascend­ing fifths, then the series “do, fa, si♭, mi♭” of descend­ing fifths.

In the sec­ond solu­tion, we direct­ly cre­ate the series “mi♭, si♭, fa, do, sol, re, la, mi, si, fa#, do#, sol#” of ascend­ing fifths, giv­ing the graph shown below.

This tun­ing is cor­rect but it can­not be used by the Bol Processor con­sole because of the shift of the ref­er­ence. Complicated pro­ce­dures would be required to set the dia­pa­son (A4 fre­quen­cy) to the desired stan­dard and to assign the cor­rect key num­bers to the notes of the scale.

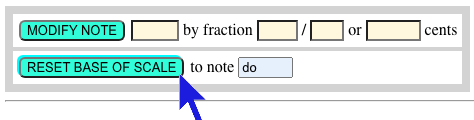
Fortunately, this prob­lem is solved in a sin­gle click by reset­ting the base of the scale to note “do”, which amounts to a rota­tion of the graph.

We take this oppor­tu­ni­ty to replace the Italian/French note con­ven­tion with the English note convention.

The result is the clas­sic mean­tone scale tun­ing which is notable for its large num­ber of har­mon­ic major thirds (cir­ca 5/4, green lines):

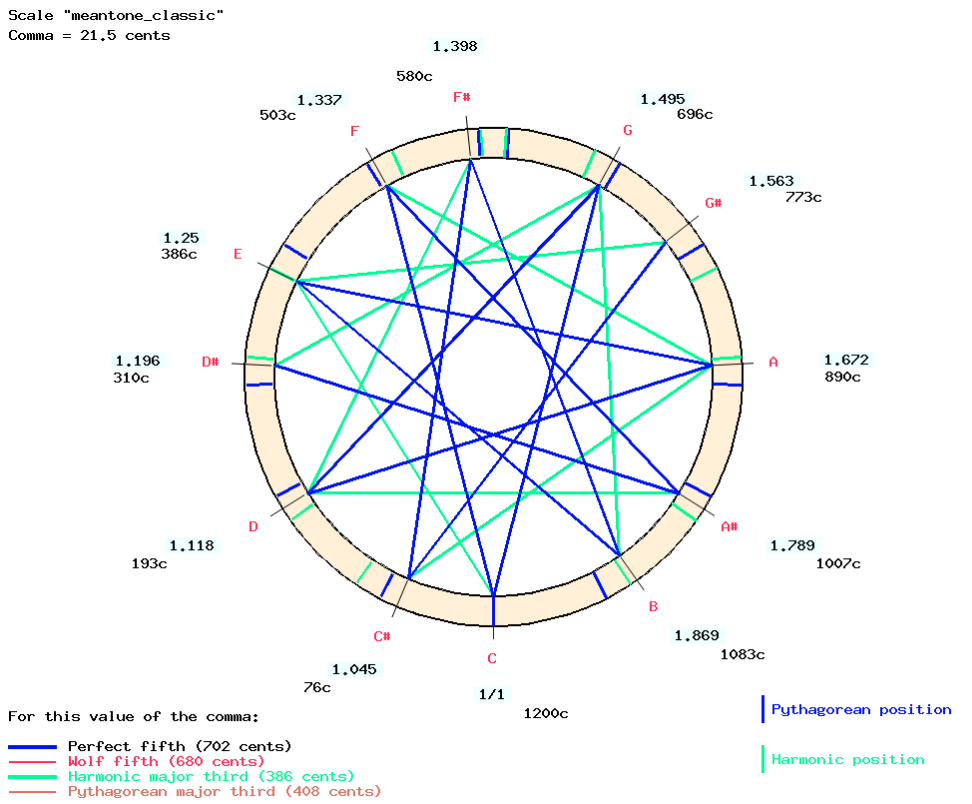
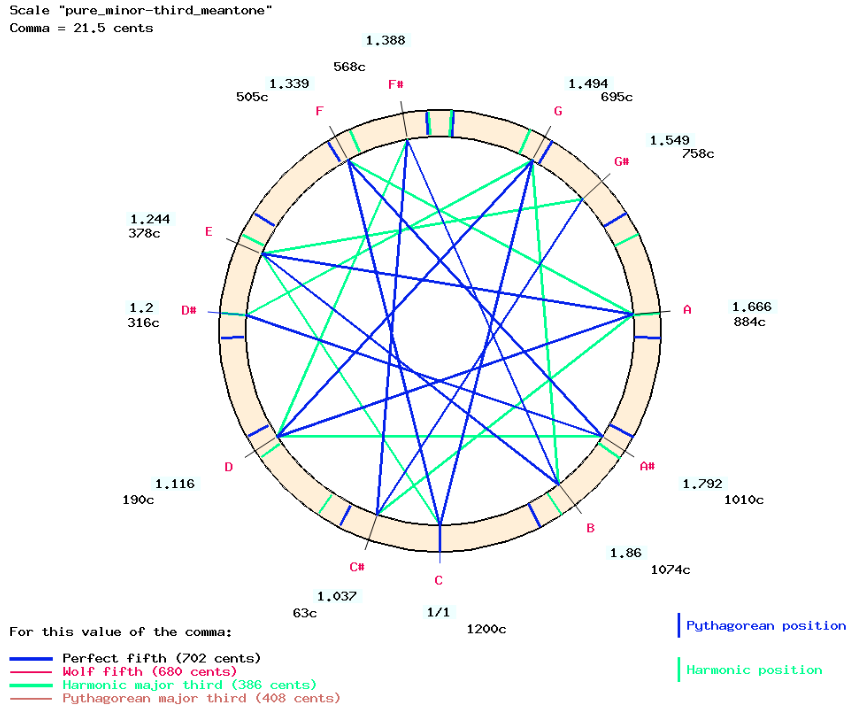
The same meth­ods can be used to imple­ment anoth­er mean­tone tem­pera­ment pop­u­lar at the same time (16^th-17^th cen­tu­ry) which aims to enhance pure minor thirds (Asselin 2000 p. 83). It can also be described as a series of ascend­ing fifths from “mi♭” to “sol#” with a dif­fer­ent adjust­ment: the fifths are dimin­ished by 1/3 comma.

In this tun­ing, the minor thirds are sized 316 cents (har­mon­ic minor third, fre­quen­cy ratio 6/5) with the excep­tion of “A#-C#”, “D#-F#” and “F-G#” which are all 352 cents:

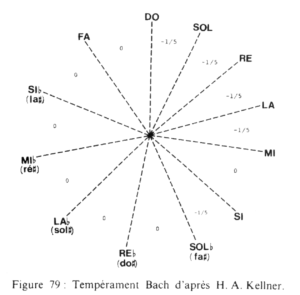
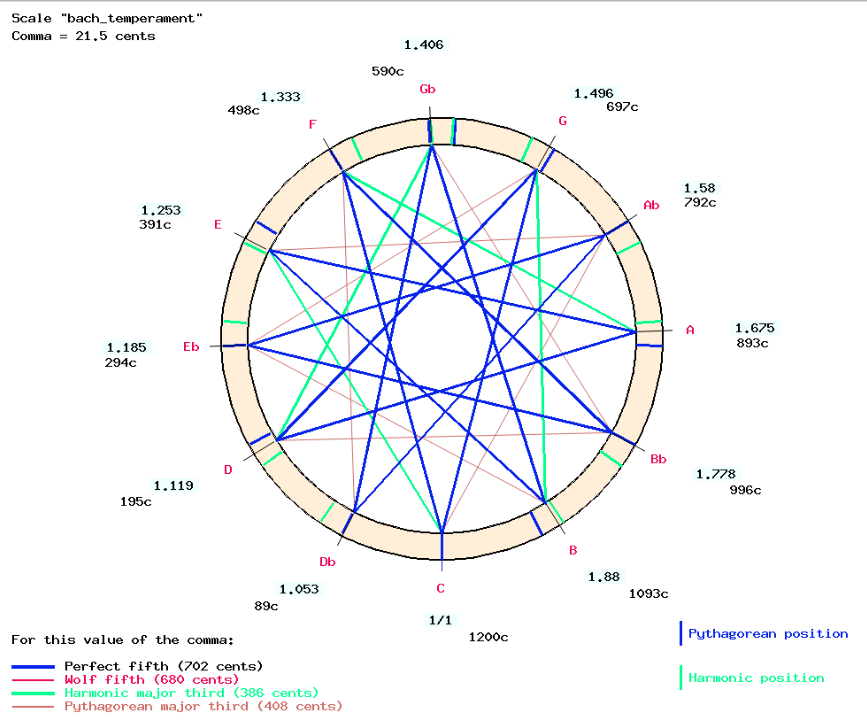
The BACH tem­pera­ment designed by Johann Peter Kellner for the music of the 18^th cen­tu­ry (Asselin 2000 p. 101-103) con­tains two vari­eties of fifths (see tun­ing scheme). It is there­fore not a “mean­tone” temperament.

It can be pro­grammed in 3 steps:

1. A series of descend­ing fifths from “do-sol-re-la-mi”, dimin­ished by 1/5 comma;
2. A series of ascend­ing per­fect fifths from “do” to “sol♭”;
3. An ascend­ing per­fect fifth from “mi” to “si”.

The last inter­val is a remain­ing fifth “si-sol♭” (“B-G♭”) dimin­ished by exact­ly 1/5 com­ma (i.e. 697 cents).

The result is close to Werkmeister III (1691) (Asselin 2000 p. 94), with all posi­tions close to the Pythagorean/harmonic series used for just into­na­tion.

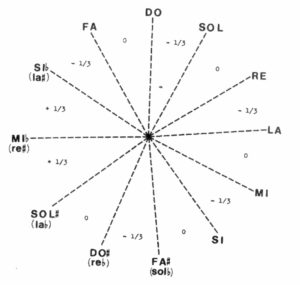
The pro­ce­dures for tun­ing tem­pera­ments with the Bol Processor some­times dif­fer from those used for phys­i­cal instru­ments. Examples are Werckmeister IV (Asselin 2000 p. 96) and Werckmeister V (p. 99). To tune Werckmeister IV on an instru­ment (see pic­ture), we start by tun­ing the sequence G C F Bb Eb Ab Db Gb B E as per­fect descend­ing fifths. Then inter­po­late three fifths (dimin­ished by 1/3 com­ma) between G and E. Then retune G so that G D becomes a per­fect fifth, which reduces C G by 1/3 com­ma. The same is done on E so that A E becomes a per­fect fifth and E B is dimin­ished by 1/3 com­ma. Similar adjust­ments are made to retune Bb, and final­ly Ab and Db to obtain the inter­vals shown on the picture.

On the Bol Processor the same pro­ce­dure can be fol­lowed if the 1/3 com­ma cor­rec­tion is replaced by 7 cents. Another pro­ce­dure is to “add” inter­vals, which is accept­able on a dig­i­tal mod­el because of the accu­ra­cy. This pro­ce­dure is auto­mat­i­cal­ly sum­marised at the bot­tom of the “scale” page:

Werckmeister IV tem­pera­ment (Asselin 2000 p. 96)
Added fifths down: “do,fa” start­ing frac­tion 1/1
Created mean­tone down­ward notes “fa,sib” frac­tion 3/2 adjust­ed -1/3 com­ma
Created mean­tone down­ward notes “sib,mib,sol#” frac­tion 3/2 adjust­ed 1/3 com­ma
Created mean­tone down­ward notes “sol#,do#” frac­tion 3/2
Created mean­tone down­ward notes “do#,fa#” frac­tion 3/2 adjust­ed -1/3 com­ma
Created mean­tone down­ward notes “fa#,si” frac­tion 3/2
Created mean­tone down­ward notes “si,mi” frac­tion 3/2 adjust­ed -1/3 com­ma
Created mean­tone down­ward notes “mi,la” frac­tion 3/2
Created mean­tone upward notes “do,sol” frac­tion 3/2 adjust­ed -1/3 com­ma
Created mean­tone upward notes “sol,re” frac­tion 3/2

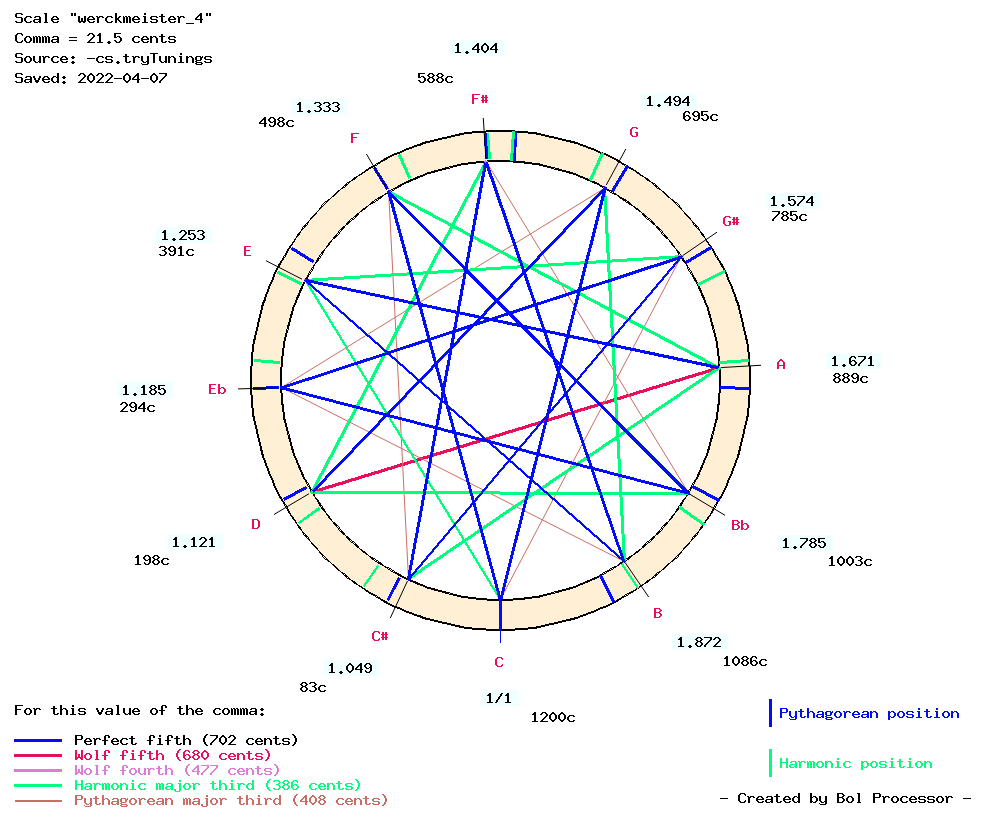
Let us com­pare some tem­pera­ments on ascend­ing unal­tered and descend­ing altered scales…

Eighteen tem­pera­ments described by Pierre-Yves Asselin (2000) have been pro­grammed in the “-cs.trTunings” Csound resource. These can be checked against var­i­ous musi­cal works, see the pages Comparing tem­pera­ments and Tonal analy­sis of musi­cal works.

As Schlick’s tem­pera­ment is not ful­ly doc­u­ment­ed, we have set “do-la♭” as a pure major third and “mi-sol#” as a major third aug­ment­ed by a 2/3 com­ma. As a result, “sol#” and “la♭” remain distinct.

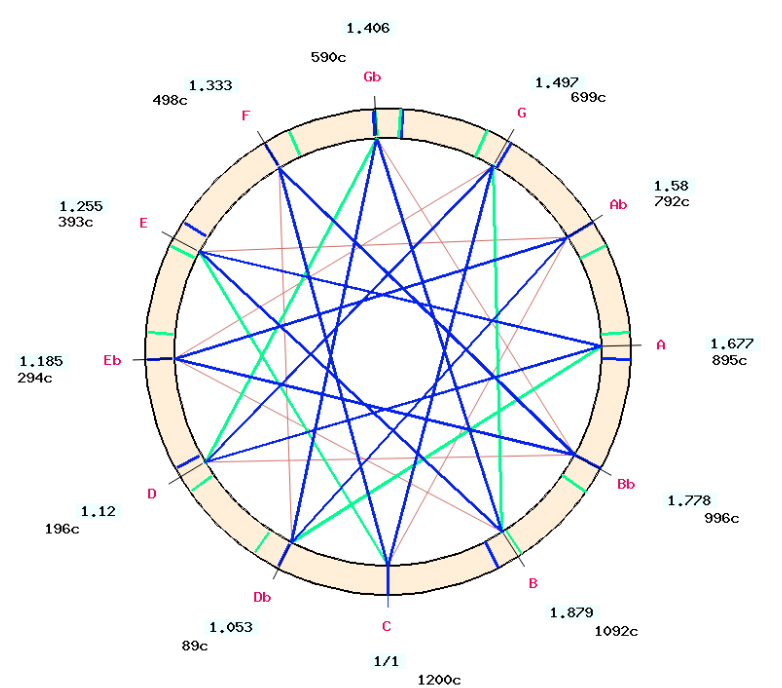
Implementations of tem­pera­ments in the Bol Processor can­not be used as a ref­er­ence because (1) errors may have occurred and (2) it is impor­tant to know the musi­cal reper­toire for which each tem­pera­ment was designed. See also chap­ter VIII of Musique et tem­péra­ments (Asselin 2000 p. 139-180) for the his­to­ry of tem­pera­ments and­mu­si­cal exam­ples dis­cussed in terms of instru­ment tuning.

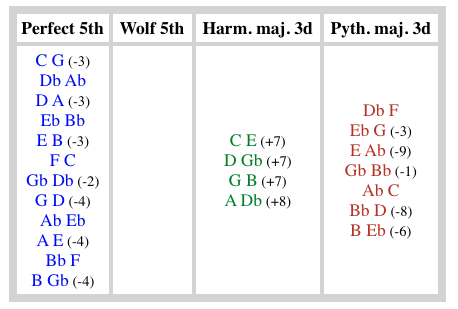
Circular graphs show notice­able inter­vals - per­fect fifths, wolf’s fifths, har­mon­ic and Pythagorean major thirds - in a wide range of uncer­tain­ty. For exam­ple, in the Tartini-Vallotti tem­pera­ment shown above, “C-E” is list­ed as a har­mon­ic major third (green seg­ment), although it is slight­ly larg­er (+7 cents) than a “pure” major third (ratio 5/4). The safe way to check that this tem­pera­ment match­es its descrip­tion is to read the devi­a­tions in the inter­val list (see picture).

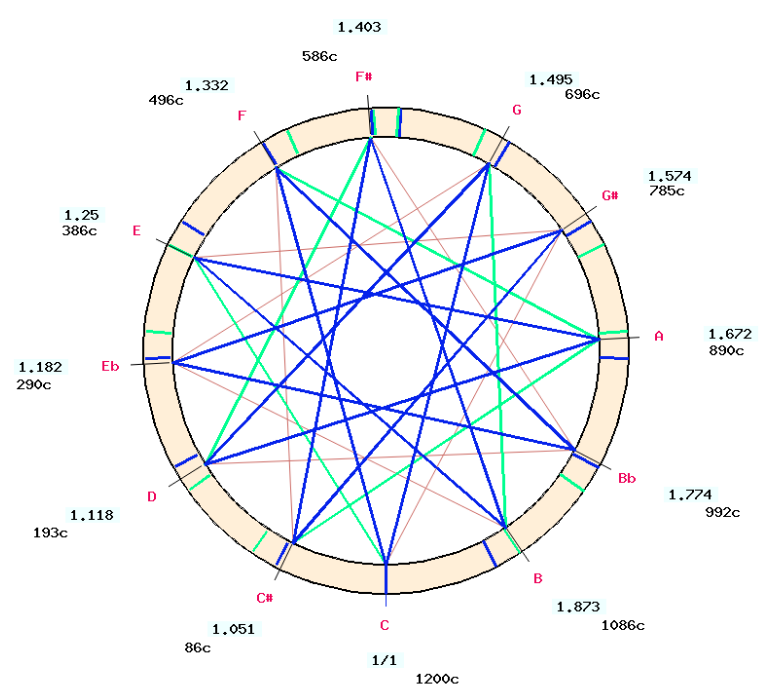
In a few tem­pera­ments the sizes of the fifths are not giv­en explic­it­ly, as the tuner is instruct­ed to tune slight­ly larg­er (than per­fect) or slight­ly small­er fifths. This is the case in the D’Alembert-Rousseau tem­pera­ment (Asselin 2000 p. 119), where the series “do, fa, sib, mi♭, sol#” is expect­ed to be slight­ly larg­er and “sol#, do#, fa#, si, mi” slight­ly small­er… In addi­tion, the frame should be “com­plete”, which implies the absence of a remain­ing com­ma frac­tion when clos­ing the cycle of fifths.

In this exam­ple, the con­di­tions were met by increas­ing the slight­ly larg­er fifths “do, fa, sib, mi♭, sol#” by 1/12 com­ma (+2 cents). To com­plete the cycle, the last series “sol#, do#, fa#, si, mi” was declared as equalised inter­vals. This result­ed in the slight­ly small­er fifths being reduced by 2 cents to reflect the slight­ly larg­er ones. Incidentally, this -1/12 com­ma adjust­ment is also the one required to con­struct an equal-tempered scale.

The whole process of cre­at­ing a scale is auto­mat­i­cal­ly record­ed in the Comments sec­tion of the “scale” page, for exam­ple “d_alembert_rousseau”:

D’Alembert-Rousseau tem­pera­ment (Asselin 2000 p. 119)
Created mean­tone upward notes “do,sol,re,la,mi” frac­tion 3/2 adjust­ed -1/4 com­ma
Created mean­tone down­ward notes “do,fa,sib,mib,sol#” frac­tion 3/2 adjust­ed 1/12 com­ma
Equalized inter­vals over series “sol#,do#,fa#,si,mi” approx frac­tion 2/3 adjust­ed 2.2 cents to ratio = 0.668

It took us about 8 min­utes to under­stand the pro­ce­dure and anoth­er 8 min­utes to tune the scale accord­ing to D’Alembert-Rousseau…

For a com­par­i­son of tem­pera­ments applied to sev­er­al pieces of Baroque music, see the page Comparing tem­pera­ments.

The full set of tun­ing schemes cur­rent­ly imple­ment­ed on the Bol Processor is pre­sent­ed on this page : https://bolprocessor.org/misc/figs/list-scales.php

More than 12 degrees

We will use a mod­el from ancient Indian musi­col­o­gy to demon­strate divi­sions of more than 12 degrees per octave. This mod­el is an inter­pre­ta­tion of the descrip­tion of the basic scales (gra­ma) and their trans­po­si­tions (mur­ccha­na) in Bharata Muni’s Natya Shastra, a trea­tise dat­ing from a peri­od between 400 BCE and 200 CE — read the page The two-vina exper­i­ment.

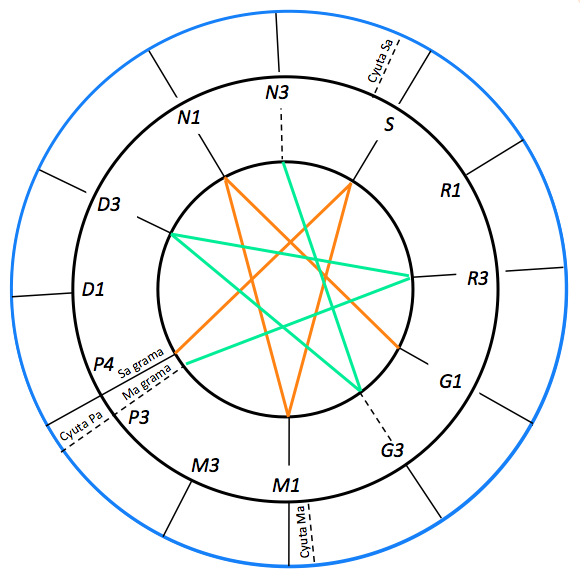
The grama-murcchana mod­el and its appli­ca­tion to west­ern har­mo­ny is described on the page Just into­na­tion: a gen­er­al frame­work. Its appli­ca­tion to Hindustani music is pre­sent­ed on the page Raga into­na­tion.

E.J. Arnold (1982) had designed a device to demon­strate the trans­po­si­tion of scales in Bharata’s mod­el. The actu­al divi­sion of the octave is 23 steps, but this amounts to hav­ing 22 option­al posi­tions (shru­ti-s) since the base note has only one option.

The result can be described as 11 pairs of note posi­tions giv­ing 2¹¹ = 2048 pos­si­ble chro­mat­ic scales. Of these, only 12 are “opti­mal­ly con­so­nant”, i.e. with only one “wrong” major fifth (short by 1 syn­ton­ic com­ma = 22 cents). These 12 scales are the ones that can be used in har­mon­ic or modal music to expe­ri­ence the best consonance.

Below is a pic­ture of the “gra­ma” scale as dis­played by the BP3 editor:

In this scale we use the con­ven­tion­al Indian sargam nota­tion: sa, re, ga, ma , pa, dha, ni, trans­lat­ed as “C”, “D”, “E”, “F”, “G”, “A”, “B”. Note that “re” (“D”), for exam­ple, can be found in four posi­tions: r1 and r2 are the two pos­si­bil­i­ties for “D♭”, the first one (256/243) being called “Pythagorean” (derived from five descend­ing fifths) and the sec­ond one (16/15) “har­mon­ic” (derived from one descend­ing fifth and one descend­ing major third). Positions r2 and r3 are “D♮” (nat­ur­al) with r3 being har­mon­ic (10/9) and r4 being Pythagorean (9/8).

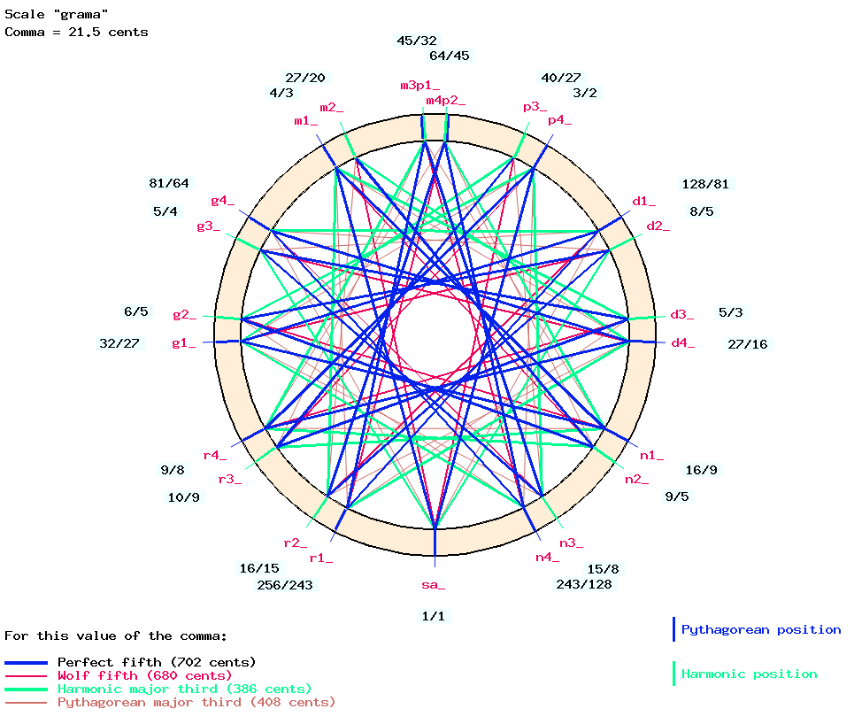
There are spe­cial cas­es (vis­i­ble on the wheel mod­el) where m3 is almost super­im­posed on p1 and m4 with p2, their dif­fer­ence being an inaudi­ble schis­ma (32805 / 32768 = 1.00112 = 1.9 cents). We use m3p1 and m4p2 to denote these merged positions.

The inter­vals giv­en in cents are those iden­ti­fied by west­ern musi­col­o­gists: the Pythagorean lim­ma (256/243 = 90 cents), the syn­ton­ic com­ma (81/80 = 22 cents) and the minor semi­tone (25/24 = 70 cents). This shows that a shru­ti, as described by Bharata, can be of 3 dif­fer­ent sizes. However, in its appli­ca­tion to Indian music, this mod­el should be ren­dered “flex­i­ble” with a size of the syn­ton­ic com­ma (pramāņa ṣru­ti) between 0 and 56.8 cents — see page The two-vina exper­i­ment.

Clicking on the IMAGE link dis­plays a cir­cu­lar graph­ic rep­re­sen­ta­tion of the “gra­ma” scale:

Let us play a dia­ton­ic scale accord­ing to the grama-murcchana mod­el, an occur­rence of west­ern just-intonation scales, and the piano stretched-octave tun­ing, again with “C4” (or “sa_4”) as the block key. The gram­mar is called “-gr.tryShruti”:

S --> _tempo(2) _scale(grama, sa_4) sa_4 r4_4 g3_4 m1_4 p4_4 d3_4 n3_4 sa_5 _scale(just into­na­tion, C4) C4 D4 E4 F4 G4 A4 B4 C5 _scale(piano, C4) do4 re4 mi4 fa4 sol4 la4 si4 do5

The dif­fer­ences are bare­ly per­cep­ti­ble for a sim­ple rea­son: the first two are iden­ti­cal, since this just into­na­tion scale is a spe­cial case of grama-murcchana, while the piano scale is a fair approx­i­ma­tion of the for­mer. This can be seen in the fol­low­ing Csound score:

Show Csound score

Let us now lis­ten to the 22 shru­tis against a drone (“C” and “G” trans­lat­ed as sa and p4):

S --> scale(grama,sa_4) {9 Full_scale _ _ _ , Drone} - - tempo(3/4) {_retro Full_scale} _ _ _
Full_scale --> sa_4 r1_4 r2_4 r3_4 r4_4 g1_4 g2_4 g3_4 g4_4 m1_4 m2_4 m3p1_4 m4p2_4 p3_4 p4_4 d1_4 d2_4 d3_4 d4_4 n1_4 n2_4 n3_4 n4_4 sa_5
Drone --> _volume(30) Droneseq Droneseq Droneseq Droneseq Droneseq Droneseq Droneseq Droneseq
Droneseq --> {_legato(300) p4_3 sa_4 sa_4 sa_3}

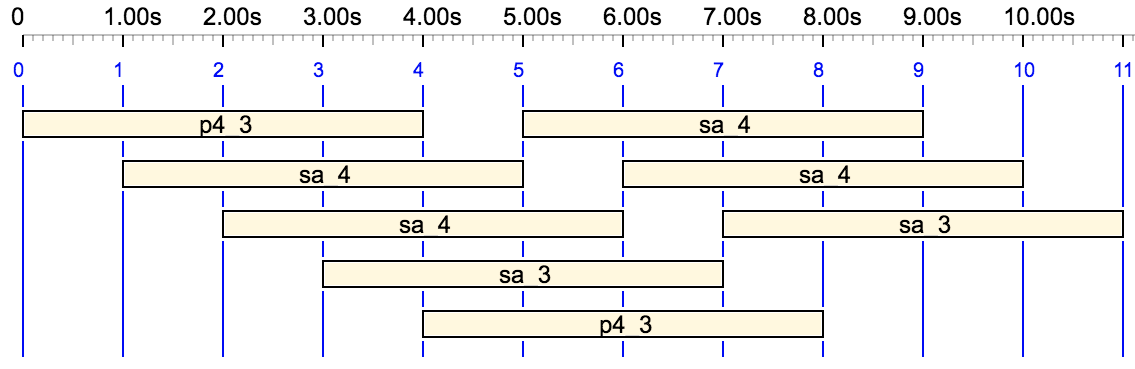
Note the use of the _retro per­for­mance tool to reverse the order of the Full_scale sequence. The _legato(300) com­mand extends the dura­tion of notes up to three times their cur­rent dura­tion. This pro­duces a Droneseq sound struc­ture sim­i­lar to that of the Indian tan­pu­ra.

In the sound ren­der­ing of this exam­ple, a 279 Hz sam­ple wave­form of a Miraj tan­pu­ra was used to feed the Karplus-Strong algo­rithm.

Show Csound score

Listening to this sequence makes it clear that treat­ing a sequence of shruti-s as a “scale” is icon­o­clas­tic for the aes­thet­ics of Hindustani music: most of these notes sound out of tune when played in rela­tion to a drone (the tan­pu­ra). As dis­cussed on page The two-vina exper­i­ment, the pres­ence of a drone makes it unlike­ly that mutu­al con­so­nance in melod­ic inter­vals will always pre­vail over con­so­nance with the drone’s upper par­tials. If the grama-murcchana sys­tem has any rel­e­vance to the per­for­mance of clas­si­cal ragas — see page Raga into­na­tion — then at the very least the mod­el should be made flex­i­ble enough to accom­mo­date the cor­rect into­na­tion in melod­ic movements.

Comparing scales

A scale com­par­i­son tool is avail­able on the Csound resource page. Click on COMPARE TONAL SCALES and select the ones that need to be analysed.

Scales are com­pared 2 by 2, so that a set of n scales gives n²/2 results, which are dis­played in tables. The fol­low­ing is a com­par­i­son of scales called Amin, Cmaj and equal_tempered. The first two ones are described on the page Just into­na­tion: a gen­er­al frame­work.

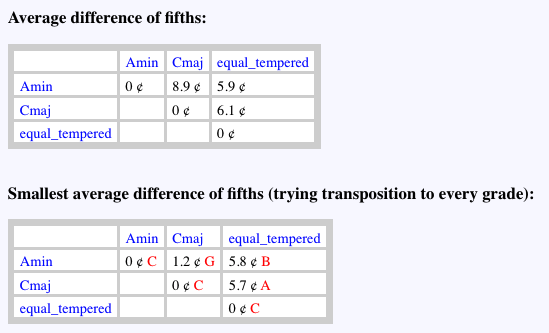
All com­par­isons are made on a 12-degree (chro­mat­ic) scale, mea­sur­ing the sizes of per­fect fifths — some of which may be wolf”s fifths as explained on the just into­na­tion page. The aver­age dif­fer­ence of fifths is cal­cu­lat­ed by sum­ming the squares of the dif­fer­ences between the sizes of fifths of iden­ti­cal degrees (count­ed in cents):

\[D=\ \sqrt{\frac{\sum_{^{i=1}}^{12}\left(fa_i\ -\ fb_i\right)^2}{12}}\]

The dis­tance between Amin and Cmaj is 8.9 cents and the dis­tance between each of these scales and the equal-tempered one is almost 6 cents.

The sec­ond table is the result of a search for the small­est dis­tance when trans­pos­ing one of the scales by 1 to 11 semi­tones. Here we see that Amin (see pic­ture) and Cmaj (see pic­ture) are prac­ti­cal­ly equiv­a­lent — they are har­mon­i­cal­ly relat­ed — since the dif­fer­ence goes down to 1.2 cents. The best match­ing ver­sion of Cmaj is con­struct­ed by trans­pos­ing Amin up a fifth (7 semi­tones), thus mov­ing ‘C’ to ‘G’. For details of this pro­ce­dure, see the sec­tion on Creation of just-intonation scales.

This device can be fur­ther devel­oped to pro­duce a clas­si­fi­ca­tion of select­ed tonal scales high­light­ing similar/identical tun­ing schemes.

Another approach to tonal scale com­par­i­son is to assess the con­cor­dance between a musi­cal work and the full set of doc­u­ment­ed tun­ing pro­ce­dures: read the page Tonal analy­sis of musi­cal works.

The syntactic model

The fol­low­ing are guide­lines for a cor­rect and use­ful imple­men­ta­tion of micro­ton­al scales in BP3. We fol­low sim­ple sequences list­ed in “-gr.tryOneScale”. This gram­mar is linked to “-cs.tryOneScale” which con­tains a unique just into­na­tion scale with its notes labelled “Cj”, “Cj#”, “Dj” etc. In “-se.tryOneScale”, the Note con­ven­tion has been set to 0 (English), the ‘C4’ key num­ber to 60 and the Default block key to 60. All these para­me­ters are impor­tant to repro­duce the same effects.

Rule #1: If only 1 micro­ton­al scale is loaded with the gram­mar, it will be used by default in all productions.

Example: Let us play:

S --> C4 A4 G4

It pro­duces the fol­low­ing Csound score:

i1 0.000 1.000 261.630 90.000 90.000 0.000 0.000 0.000 0.000 ; Cj4
i1 1.000 1.000 436.137 90.000 90.000 0.000 0.000 0.000 0.000 ; Aj4
i1 2.000 1.000 392.445 90.000 90.000 0.000 0.000 0.000 0.000 ; Gj4

The dis­play of “Cj4” etc. makes it clear that just into­na­tion has been used. This is also con­firmed by ratio 436.137/261.630 = 1.666 = 5/3.

Why not use the note labels “Cj4”, “Aj“ ‘ and “Gj4” in the gram­mar? This only works if, for exam­ple, the scale is specified:

S --> _scale(just into­na­tion, Cj4) Cj4 Aj4 Gj4

This will give the same Csound score because the block key “Cj4” is set to 261.630 Hz in the scale def­i­n­i­tion. Using “Aj4” as the block key would give:

S --> _scale(just into­na­tion, Aj4) Cj4 Aj4 Gj4

and a sight­ly dif­fer­ent Csound score:

i1 0.000 1.000 263.952 90.000 90.000 0.000 0.000 0.000 0.000 ; Cj4
i1 1.000 1.000 440.007 90.000 90.000 0.000 0.000 0.000 0.000 ; Aj4
i1 2.000 1.000 395.928 90.000 90.000 0.000 0.000 0.000 0.000 ; Gj4

Here, “Aj4” has been set to 440 Hz which is the dia­pa­son fre­quen­cy in “-se.tryOneScale”. The ratios are unchanged, e.g. 440.007/263.952 = 5/3.

How can we play equal-tempered inter­vals with this gram­mar? This is achieved by spec­i­fy­ing the default scale: _scale(0,0):

S --> _scale(0,0) C4 A4 G4

yield­ing the fol­low­ing Csound score:

i1 0.000 1.000 8.00 90.000 90.000 0.000 0.000 0.000 0.000 ; C4
i1 1.000 1.000 8.09 90.000 90.000 0.000 0.000 0.000 0.000 ; A4
i1 2.000 1.000 8.07 90.000 90.000 0.000 0.000 0.000 0.000 ; G4

The fre­quen­cies are not explic­it because the default Csound score for­mat uses the octave point pitch-class rep­re­sen­ta­tion, for exam­ple “A4” is the 9^th pitch-class or the 8^th octave (on a stan­dard MIDI instru­ment). To make them explic­it, just set the dia­pa­son in “-se.tryOneScale” to a slight­ly dif­fer­ent val­ue, for exam­ple 440.0001 Hz. This will produce:

i1 0.000 1.000 261.626 90.000 90.000 0.000 0.000 0.000 0.000 ; C4
i1 1.000 1.000 440.000 90.000 90.000 0.000 0.000 0.000 0.000 ; A4
i1 2.000 1.000 391.996 90.000 90.000 0.000 0.000 0.000 0.000 ; G4

We could expect the fre­quen­cy of “C4” to be 261.630 Hz, but the val­ue of 261.626 Hz dif­fers due to round­ing. The ratio of the dif­fer­ence is 261.630/261.626 = 1.000015 = 0.026 cents!

Rule #2: When pars­ing a sequence of notes, if a micro­ton­al scale has been spec­i­fied, the pars­er will first attempt to match the note against labels in the cur­rent micro­ton­al scale. If there is no match, it will try to inter­pret the note accord­ing to the Note con­ven­tion spec­i­fied in settings.

For instance:

S --> _scale(just into­na­tion, Cj4) Cj4 Aj4 Gj4 D4 F4 E4

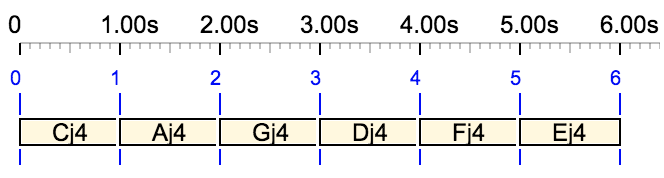
The notes in the sequence “D4 F4 E4” are trans­lat­ed to the cor­re­spond­ing posi­tions in the into­na­tion scale. The result is vis­i­ble in both the Csound score and the graphic.

This prac­tice is only rel­e­vant to 12-degree tonal scales where posi­tions are equiv­a­lent — albeit with slight­ly dif­fer­ent fre­quen­cy ratios. For exam­ple, since the match­ing is based on key num­bers, feed­ing the “gra­ma” (23-degree) micro­ton­al scale (see above) with “C4 D4 E4” would pro­duce “sa_4 r2_4 r4_4″, where r2_4 is close to “C#4” and r4_4 is close to “D4”. This makes sense because the key sequence is 60-62-64. There is cur­rent­ly no gener­ic way of map­ping note posi­tions in scales with dif­fer­ent divi­sions. An addi­tion­al dif­fi­cul­ty would be scales with an inter­val oth­er than 2/1.

We will show lat­er that rule #2 pro­vides a flex­i­bil­i­ty that makes it very easy to insert enhar­mon­ic cor­rec­tions in a musi­cal score by select­ing one of 12 just-intonation chro­mat­ic scales — see the page Just into­na­tion: a gen­er­al frame­work.

Rule #3: If the pars­er can­not iden­ti­fy a note in the cur­rent micro­ton­al scale and against the note con­ven­tion, it will try oth­er micro­ton­al scales pre­vi­ous­ly loaded in the sequence.

This can be demon­strat­ed with “-gr.tryScales”. At the top of the gram­mar are list­ed the scales that will be sent to the con­sole along with the gram­mar and instruc­tions. Each scale becomes “active” in the gram­mar once a _scale() oper­a­tor has declared it.

Let us try to produce:

S --> _scale(piano,dop4) fap3 _scale(just intonation,69) C4 rep4

Active scales are piano, then just into­na­tion. There are no prob­lems with note “fap3”, which belongs to the piano scale, nor with “C4” which is known in the English note con­ven­tion. As pre­dict­ed by rule #2, the note “C4” is trans­lat­ed to its equiv­a­lent “Cj4” and played in just intonation.

Since the baseoc­tave of the scale piano is 3 (see the image above), the pitch of “fap3” will be close to that of “F4”.

What hap­pens to note “rep4”? If the piano scale had not been acti­vat­ed, this note would be reject­ed as a syn­tax error. However, fol­low­ing rule #3, the pars­er finds it in the piano scale. This results in the key num­ber 74 since baseoc­tave = 3.

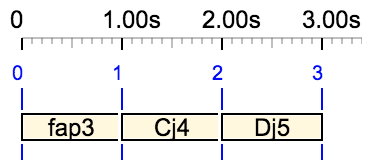
The note is inter­pret­ed as key #74 in the just into­na­tion scale, dis­played as “Dj5”. This can be seen in the Csound score below and in the graphic.

i1 0.000 1.000 349.538 90.000 90.000 0.000 0.000 0.000 0.000 ; fap3
i1 1.000 1.000 263.952 90.000 90.000 0.000 0.000 0.000 0.000 ; Cj4
i1 2.000 1.000 593.891 90.000 90.000 0.000 0.000 0.000 0.000 ; Dj5

As a result, notes found in a sequence are always inter­pret­ed as belong­ing to the scale declared imme­di­ate­ly to the left, even if their label belongs to a dif­fer­ent scale or note convention.

Therefore, it is not a good idea to mix notes belong­ing to dif­fer­ent scales with­out declar­ing the scale before they occur. A “_scale()” dec­la­ra­tion is best placed at the begin­ning of each sequence, espe­cial­ly at the begin­ning of the right argu­ment of a rule.

References

Arnold, E.J. A Mathematical mod­el of the Shruti-Swara-Grama-Murcchana-Jati System. Journal of the Sangit Natak Akademi, New Delhi 1982.

Asselin, P.-Y. Musique et tem­péra­ment. Paris, 1985, repub­lished in 2000: Jobert. Soon avail­able in English.