Creation of just-intonation scales

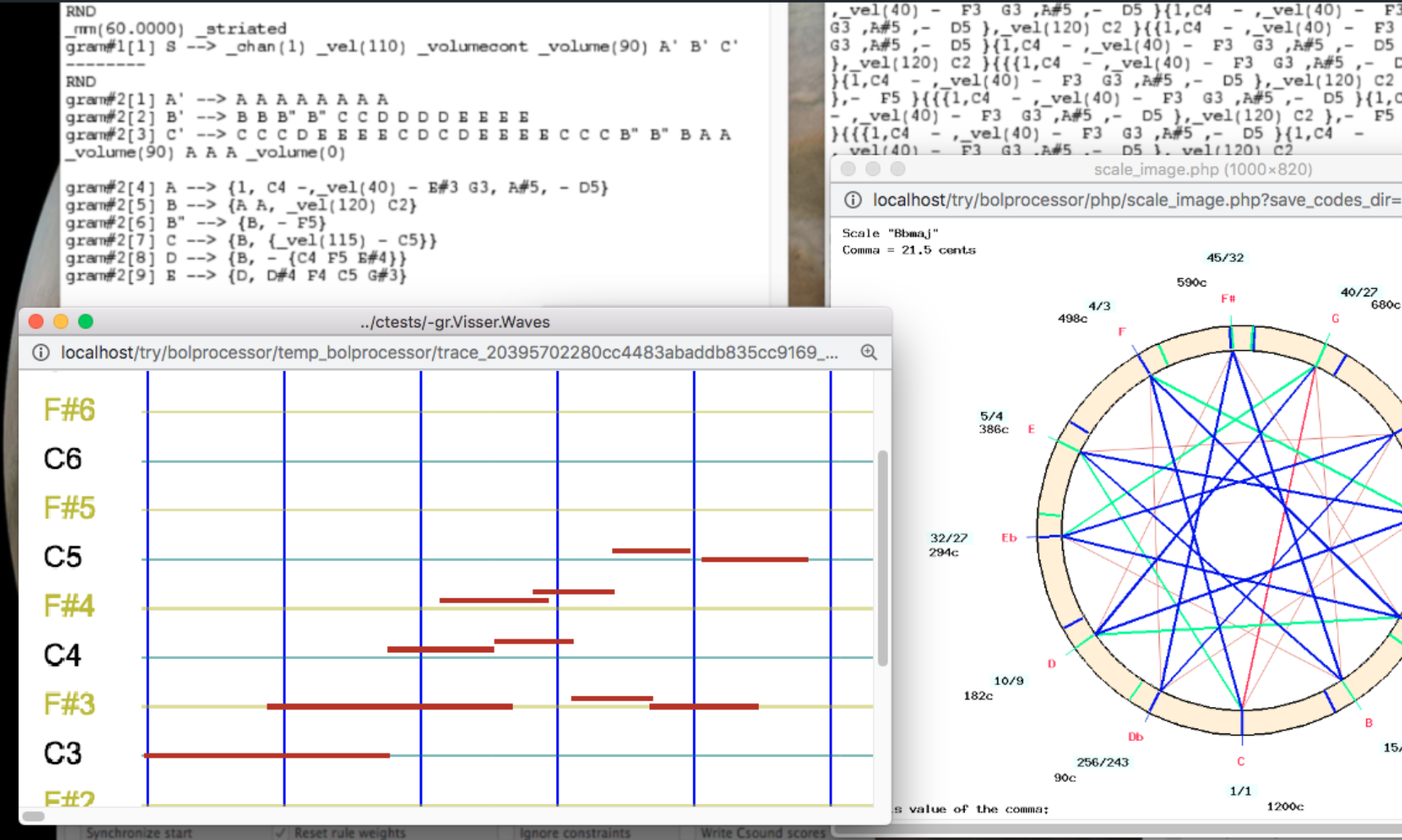
The fol­low­ing is the pro­ce­dure for export­ing just-intonation scales from the mur­ccha­na-s of Ma-grama stored in “-cs.12_scales”.

➡ Read Just into­na­tion: a gen­er­al frame­work for explanation.

The scale model

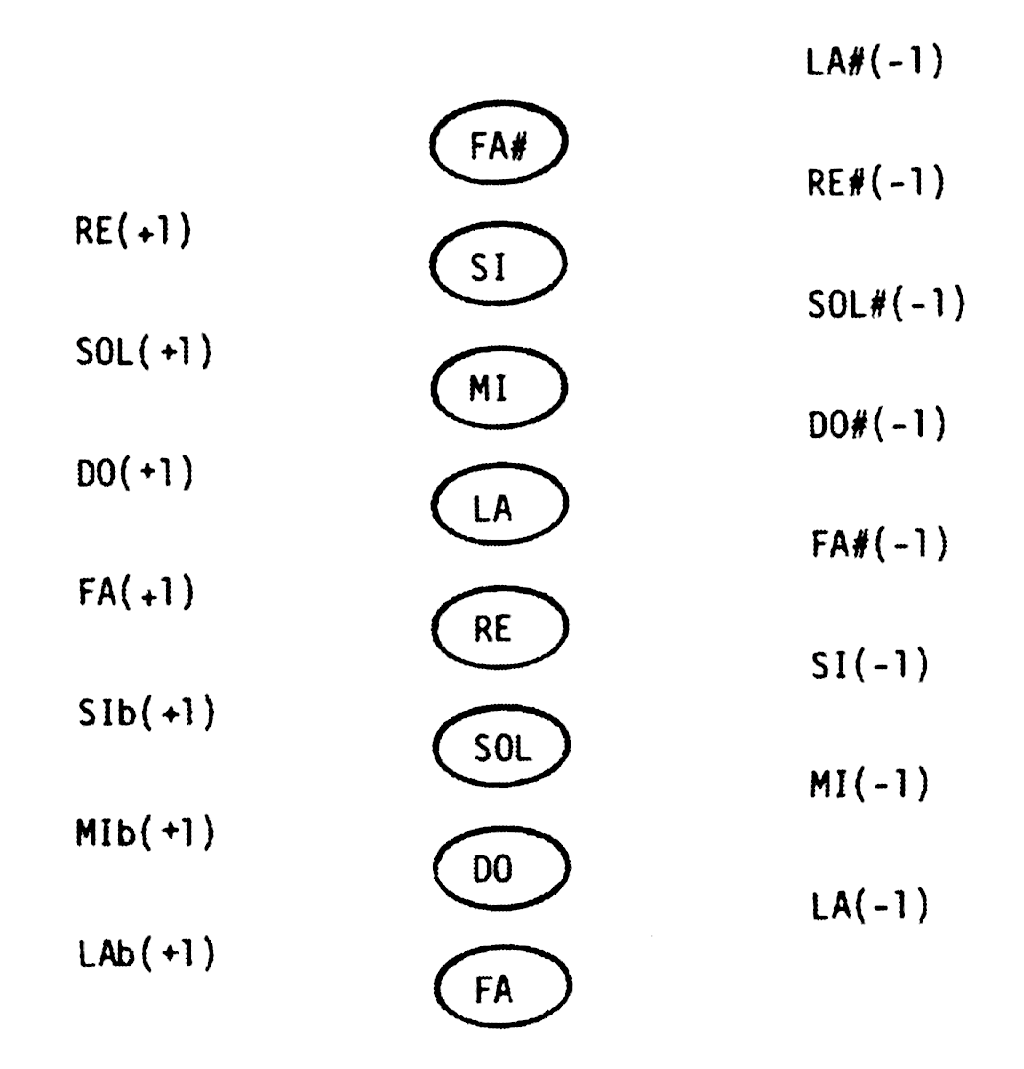
As indi­cat­ed on the page Just into­na­tion: a gen­er­al frame­work, just-intonation chro­mat­ic scales can be derived from a basic frame­work made of two cycles of per­fect fifths (fre­quen­cy ratio 3/2).

These pro­duce the 22-shru­ti frame­work of Indian musi­col­o­gists (read Raga into­na­tion) or the series called “Pythagorean” and “1^st-order ascending-third” (“LA-1”, “MI-1” etc.) in the approach of west­ern musi­col­o­gists (see pic­ture on the side).

We have found that the “1^st-order descending-third cycle” (“LAb+1”, “MIb+1” etc.), in which all notes are high­er by a syn­ton­ic com­ma may not be nec­es­sary for the cre­ation of just-intonation chords.

These cycles of fifths are rep­re­sent­ed graph­i­cal­ly (scale “2_cycles_of_fifths” in the Csound resource “-cs.tryTunings”):

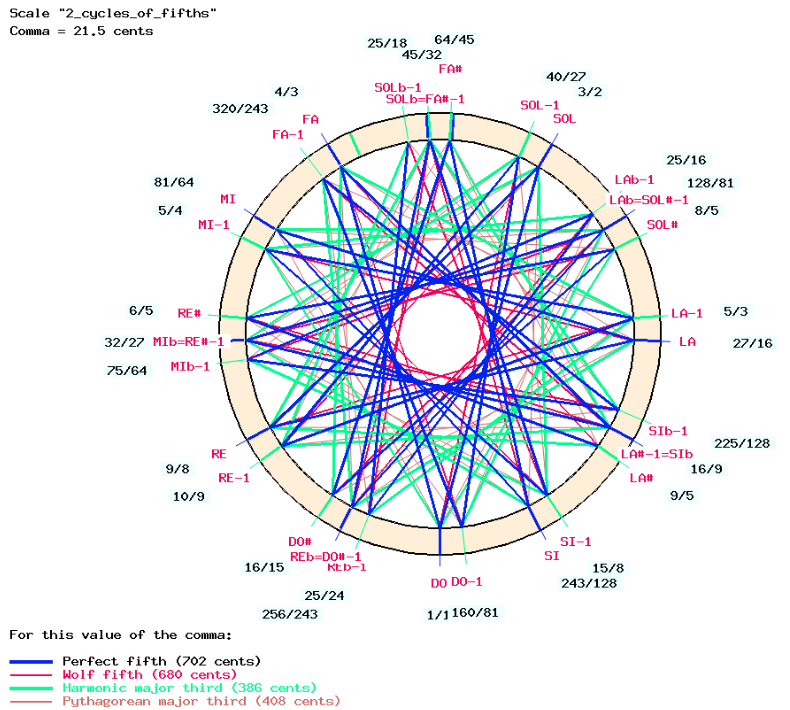
There are some dif­fer­ences between this 29-degree divi­sion of the octave and the Indian frame­work, notably the cre­ation of “DO-1” and “FA-1”, two posi­tions one syn­ton­ic com­ma low­er than “DO” (“C” = “Sa” in the Indian con­ven­tion) and “FA” (“F” = “Ma”). Interestingly, these posi­tions appear in ancient texts under the names “cyu­ta Sa” and “cyu­ta Ma”. Other addi­tion­al posi­tions are “REb-1”, “MIb-1”, “SOLb-1”, “LAb-1” and “SIb-1”.

The rule we fol­low when cre­at­ing chro­mat­ic scales from trans­po­si­tions of Ma-grama is that only the posi­tions shown on this graph are con­sid­ered valid. When export­ing a minor or major chro­mat­ic scale from a trans­po­si­tion of Ma-grama, it may hap­pen that a note posi­tion is not part of this frame­work. In all cas­es of this pro­ce­dure, the invalid posi­tion is one syn­ton­ic com­ma too low. Therefore the export­ed scale is “aligned” by rais­ing all its posi­tions by one comma.

The term “Pythagorean series” is con­fus­ing because any cycle of per­fect fifths is Pythagorean by def­i­n­i­tion. Whether a posi­tion in a scale “is” or “is not” Pythagorean depends on the start­ing note of the series that was announced as “Pythagorean”. In Asselin’s work the start­ing point of the series in the mid­dle col­umn is “FA”. In the Indian sys­tem, the basic frame­works (Ma-grama and Sa-grama) start from “Sa” (“C” or “do”) and the Pythagorean/harmonic sta­tus of a posi­tion is deter­mined by fac­tors of its fre­quen­cy ratio with respect to “Sa”. If a fac­tor “5” is found in the numer­a­tor or the denom­i­na­tor, the posi­tion is har­mon­ic or, con­verse­ly, Pythagorean.

For exam­ple, “DO#” in Asselin’s “Pythagorean” series (two per­fect fifths above “SI”) is eval­u­at­ed as a har­mon­ic posi­tion (marked in green) on the Bol Processor graph and its ratio is 16/15. In real­i­ty, “DO#” in Asselin’s series has a fre­quen­cy ratio of 243/128 * 9/16 = 2187/1024 = 1.068 which is very close to 16/15 = 1.067. “DO#-1” in Asselin’s series is two per­fect fifths above “SI-1” which gives a fre­quen­cy ratio of 15/8 * 9/16 = 135/128 = 1.054 which is close to 256/243 = 1.053 and marked “Pythagorean” on the Indian scheme. Thus, “DO#” and “DO#-1” have exchanged their prop­er­ties, each being the super­po­si­tion of two very close posi­tions belong­ing to dif­fer­ent series.

Ignoring schis­ma dif­fer­ences inn order to take the sim­plest ratios cre­ates this con­fu­sion. For this rea­son, we still pre­fer to use com­ma indi­ca­tions — e.g. “FA” and “FA-1” — to iden­ti­fy posi­tions where the first instance belongs to the series called “Pythagorean” in Asselin’s work.

Transposition table

This table sum­maris­es a quick pro­ce­dure for cre­at­ing all the mur­ccha­na-s of the Ma-grama chro­mat­ic scale and export­ing minor and major chro­mat­ic scales from them.

Open the scale “Ma_grama” in the “-cs.12_scales” Csound resource, and select the Murcchana pro­ce­dure. To cre­ate “Ma01″, move note “F” to note “C” and click on TRANSPOSITION.

F moved to	Murcchana	Minor scale	Raise	Major scale		Identical scale	Adjust
C	Ma01	Amin	D	Cmaj	=	Emin	1/1
F	Ma02	Dmin	G	Fmaj	=	Amin	1/1
Bb	Ma03	Gmin	C	Bbmaj	=	Dmin	1/1
Eb	Ma04	Cmin	F	Ebmaj	=	Gmin	1/1
Ab	Ma05	Fmin	Bb	Abmaj	=	Cmin	1/1
Db	Ma06	Bbmin	Eb	Dbmaj	=	Fmin	1/1
F#	Ma07	Ebmin	Ab	F#maj	=	Bbmin	1/1
B	Ma08	Abmin	Db	Bmaj	=	Ebmin	1/1
E	Ma09	Dbmin	F#	Emaj	=	Abmin	1/1
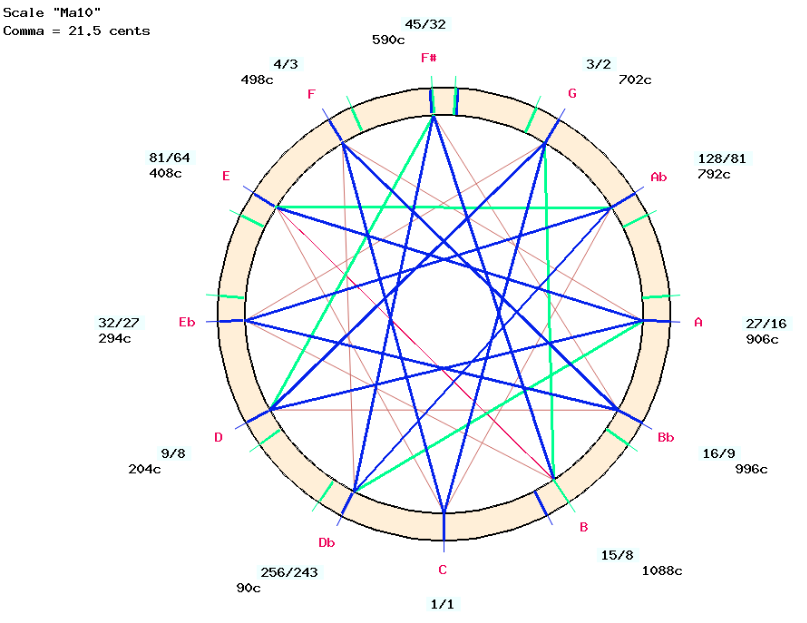
A	Ma10	F#min	B	Amaj	=	Dbmin	81/80
R3	Ma11	Bmin	E	Dmaj	=	F#min	81/80
G3	Ma12	Emin	A	Gmaj	=	Bmin	81/80

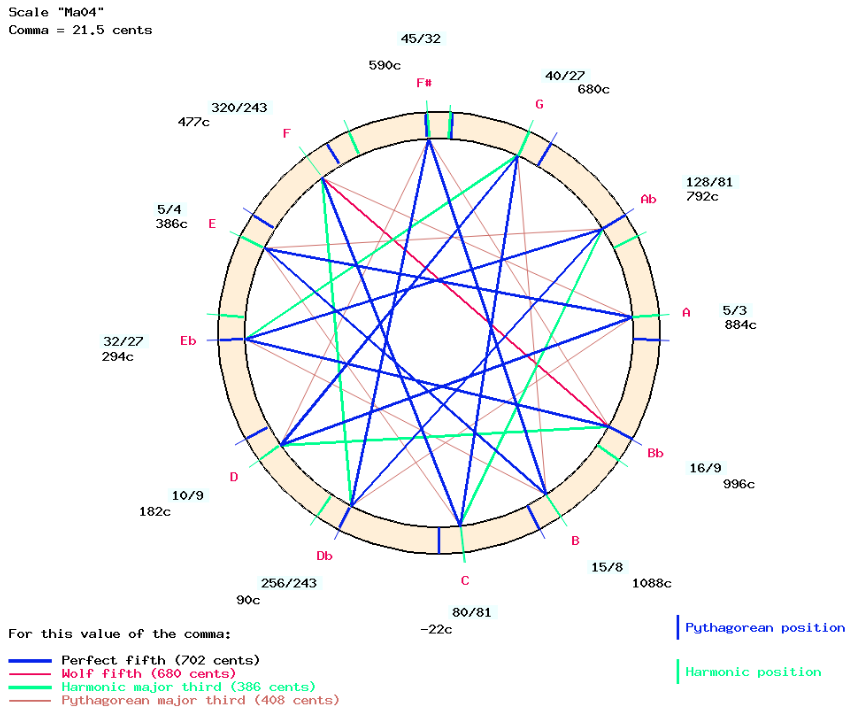
For exam­ple, this is the “Ma04″ mur­ccha­na obtained by plac­ing “F” (M1 on the Indian scale mod­el) of the mov­ing wheel on “Eb” (G1 of the out­er crown):

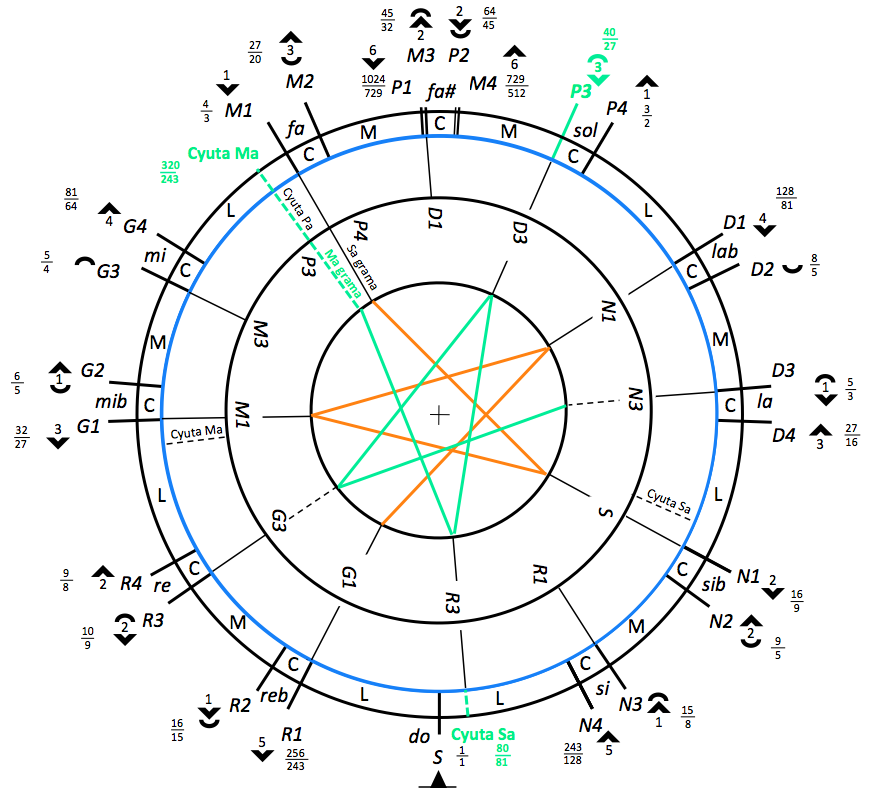
The result­ing “Ma04″ scale is:

Scale adjustment

In the last col­umn of the table, “Adjust” indi­cates the frac­tion by which the note ratios may need to be mul­ti­plied so that no posi­tion is cre­at­ed out­side the Pythagorean and har­mon­ic cycles of fifths accord­ing to the Indian sys­tem. Practically this is the case when the fre­quen­cy ratio con­tains a mul­ti­ple of 25 in either its numer­a­tor or denom­i­na­tor, as this indi­cates that the posi­tion has been con­struct­ed by at least two suc­ces­sive major thirds (up or down).

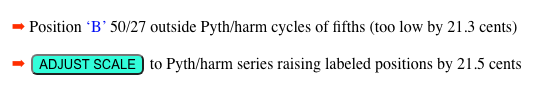
A warn­ing is dis­played if this is the case, and a sin­gle click on ADJUST SCALE fix­es the positions:

In this exam­ple, the warn­ing sig­nals an out-of-range posi­tion of “B” (50/27) on the “Ma10″ scale. Note also that “F#” has a mul­ti­ple of 25 in its numerator.

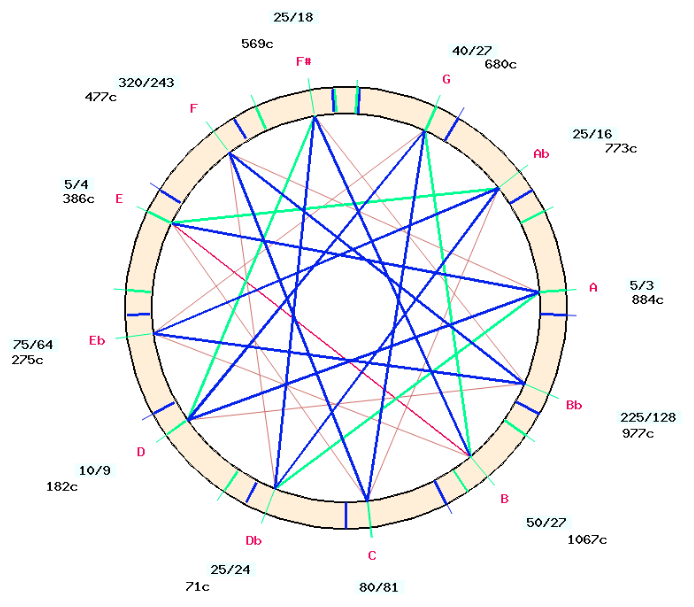
After click­ing on ADJUST SCALE, the scale “Ma10″ is com­plet­ed with “B” in posi­tion 15/8. This has been done by rais­ing all the notes by one syn­ton­ic com­ma (81/80) :

This pro­ce­dure is known in Indian musi­col­o­gy as sadja-sadharana, which means that all the notes of the scale are raised by a shru­ti — here, a syn­ton­ic com­ma (Shringy & Sharma 1978). In this mod­el, it is also invoked for the scales “Ma11″ and “Ma12″. The result is (as expect­ed) a cir­cu­lar mod­el because “Ma13″ is iden­ti­cal to “Ma01″ as shown by the scale com­para­tor at the bot­tom of page “-cs.12_scales”.

This cir­cu­lar­i­ty is a prop­er­ty of the set of mur­ccha­na-s which has no effect on export­ed minor and major scales, since their posi­tions are aligned accord­ing to the basic rule explained in the first section.

Exporting and aligning minor scales

The “Ma04″ mur­ccha­na pro­duces “Cmin” by export­ing notes fac­ing the marks on the inner wheel.

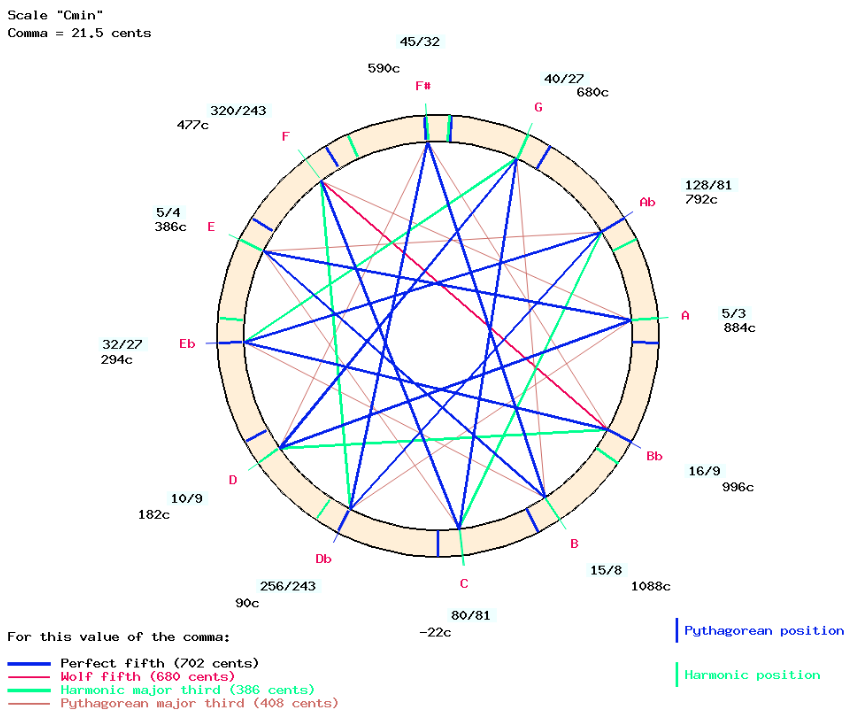
As explained on page Just into­na­tion: a gen­er­al frame­work, the ton­ic and dom­i­nant notes of each minor chord should belong to the “minus-1” posi­tion. In this exam­ple, “C” and “G” are one com­ma low­er in a “C minor” chord than in a “C major” chord (cor­re­spond­ing to “DO-1” and “SOL-1” on the “2_cycles_of_fifths” scale), a fact pre­dict­ed and exper­i­men­tal­ly ver­i­fied by Pierre-Yves Asselin (2000 p. 137).

All chro­mat­ic minor scales export­ed from the mur­chana-s of the Ma-grama are cor­rect­ly posi­tioned with respect to the enhar­mon­ic posi­tions of the main notes in just-intonation chords. This can be eas­i­ly checked by com­par­ing the ratios with those asso­ci­at­ed with the west­ern series on “2_cycles_of_fifths” (top of this page). This con­firms that a tun­ing sys­tem using only two series of per­fect fifths is suit­able for the con­struc­tion of a just-intonation framework.

Exporting and aligning major scales

The “Ma04″ mur­ccha­na pro­duces “Ebmaj” by export­ing notes fac­ing the marks on the inner wheel and rais­ing “F”:

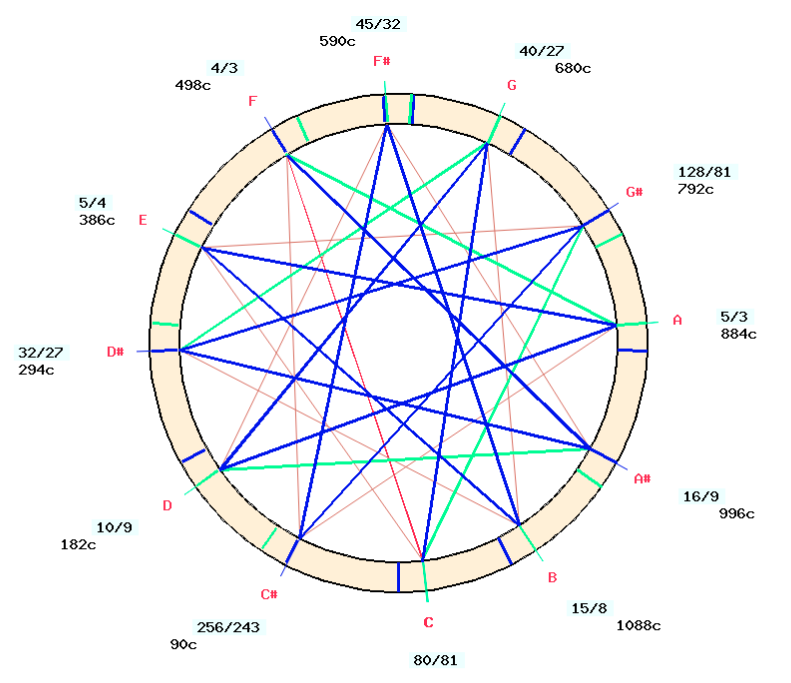
According to a rule explained on the page Just into­na­tion: a gen­er­al frame­work, the root of each major chord should be both in the high posi­tion and in the Pythagorean series (blue mark­ings). This is true for the chord “Eb major” tak­en from the chro­mat­ic scale “Ebmaj”, but not for the scales “F#maj”, “Bmaj” and “Emaj” shown in bold on the table.

For exam­ple, let us look at “Emaj”, which was export­ed from “Ma09″ with­out any precautions:

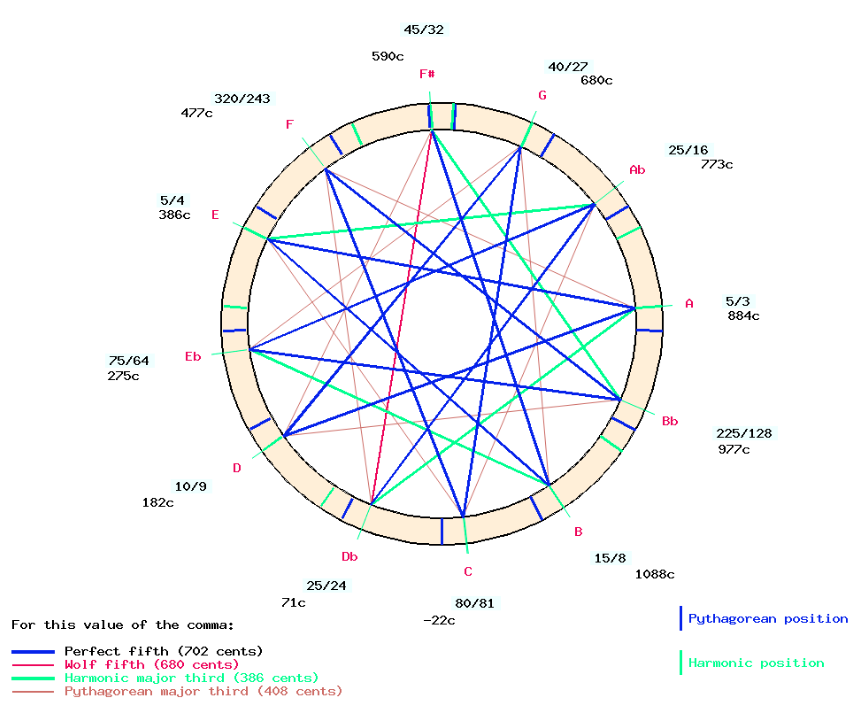
The note “E” has a fre­quen­cy ratio of 5/4, which is labelled “MI-1” on the scale “2_cycles_of_fifths” (top of this page). Since “MI-1” belongs to a har­mon­ic series, it can­not be tak­en as a the ton­ic of an “E major chord”. The Pythagorean “MI” (ratio 81/64) should be used instead.

After its adjust­ment — rais­ing all notes by 1 syn­ton­ic com­ma — the final “Emaj” scale is obtained:

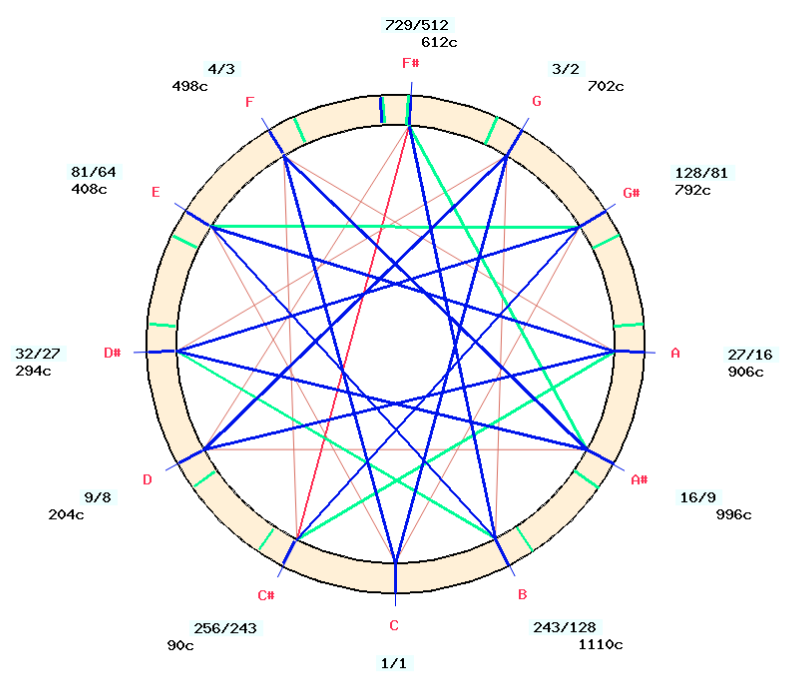
This align­ment of export­ed major scales is done auto­mat­i­cal­ly by the Bol Processor when export­ing a major chro­mat­ic scale.

References

Asselin, P.-Y. Musique et tem­péra­ment. Paris, 1985, repub­lished in 2000: Jobert. Soon avail­able in English.

Shringy, R.K.; Sharma, P.L. Sangita Ratnakara of Sarngadeva: text and trans­la­tion, vol. 1, 5: 7-9. Banaras, 1978: Motilal Banarsidass. doi:10.2307/2054840. Source in the Web Archive.