Harm Visser’s examples

In Computer Music Journal 22,2 (1998) page 63, Dutch com­pos­er Visser commented:

I think that the devel­op­ment of more and more visu­al stuff cur­tails the pos­si­bil­i­ty of “think­ing in your chair.” Sometimes I devel­op gram­mars, not at the com­put­er, but sit­ting with a pen­cil and paper. With pro­grams [oth­er than BP2] this is not pos­si­ble: you must sit in front of the com­put­er. The dif­fer­ence lies in the type of atten­tion that each soft­ware envi­ron­ment demands on the part of the com­pos­er, and indeed reflects on the way s/he thinks about music.

The fol­low­ing is a pre­sen­ta­tion and dis­cus­sion of a few exam­ples com­posed on Bol Processor by Harm Visser in 1998. All exam­ples shown on this page are avail­able in the sam­ple set bp3-ctests-main.zip shared on GitHub. Follow instruc­tions on page Bol Processor ‘BP3’ and its PHP inter­face to install BP3 and learn its basic oper­a­tion. Download and install Csound from its dis­tri­b­u­tion page.

Period notation

In the same way it deals with super­im­posed sequences, the poly­met­ric expan­sion algo­rithm works out equal sym­bol­ic dura­tions between beat sep­a­ra­tors notat­ed ‘•’ — name­ly the peri­od nota­tion.  A note sequence in peri­od nota­tion and the context-free gram­mar it orig­i­nat­ed from are shown below.  In this exam­ple, beats con­tain increas­ing num­bers of notes result­ing in an accel­er­at­ing movement.

S --> _vel(60) A B _vel(65) C D _vel(70) E F _vel(75) G _vel(77) H _vel(80) I _vel(85) J _vel(87) K _vel(90) L
A --> E2 •
B --> D2 A
C --> B2 B
D --> G2 C
E --> F#2 D
F --> A#2 E
G --> C2 F
H --> G#2 G
I --> A2 H
J --> D#2 I
K --> C#2 J
L --> F2 K

The “_vel” oper­a­tor is a con­trol of veloc­i­ty pro­duc­ing a step­wise increas­ing vol­ume of the piece. This gram­mar yields the fol­low­ing “score”:

_vel(60) E2 • D2 E2 •_vel(65) B2 D2 E2 • G2 B2 D2 E2 • _vel(70) F#2 G2 B2 D2 E2 • A#2 F#2 G2 B2 D2 E2 • _vel(75) C2 A#2 F#2 G2 B2 D2 E2 • _vel(77) G#2 C2 A#2 F#2 G2 B2 D2 E2 • _vel(80) A2 G#2 C2 A#2 F#2 G2 B2 D2 E2 • _vel(85) D#2 A2 G#2 C2 A#2 F#2 G2 B2 D2 E2 • _vel(87) C#2 D#2 A2 G#2 C2 A#2 F#2 G2 B2 D2 E2 • _vel(90) F2 C#2 D#2 A2 G#2 C2 A#2 F#2 G2 B2 D2 E2 •

and the fol­low­ing piano-roll rep­re­sen­ta­tion with the sound exam­ple on a Pianoteq syn­the­siz­er:

Serial tools

The fol­low­ing gram­mar pro­duces a 10-minute musi­cal piece with only 12 rules and 3 notes (C3, D4, F#3). It is an illus­tra­tion of Visser’s mot­to: “com­pos­ing with a pen­cil and paper”.

The rhyth­mic intri­ca­cy is the result of using poly­met­ric expres­sions: super­im­po­si­tion of sequences list­ed between curled brack­ets {} and resiz­ing “beats” thanks to the peri­od mark­er ‘•’.

The length and com­plex­i­ty of the piece is achieved by the use of recur­sive rules. For instance, rule gram#2[2] pro­duces “Mel1” that will be rewrit­ten again by rule gram#2[1].

Three “ser­i­al tools” are used:

• _transpose(n) shifts up the fol­low­ing sequence by n semitones
• _rotate(x) rotates the fol­low­ing sequence by x units
• _keyxpand(basenote, ratio) mul­ti­plies melod­ic inter­vals with ratio rel­a­tive to basenote. For instance, after _keyxpand(C4, 2), sequence D4 E4 F4 would be replaced with E4 G#4 Bb4. This tool is applied recur­sive­ly to the fields of a poly­met­ric expres­sion.

Show grammar

Note that all sub­gram­mars are head­ed with “ORD”, mean­ing that rules will be applied in order instead of being ran­dom­ly select­ed. Thus, this gram­mar pro­duces a unique musi­cal piece, which is the case with all exam­ples com­posed by Harm Visser. The only sto­chas­tic ele­ment of this piece is the veloc­i­ty that may vary between 60 and 100 due to per­for­mance con­trols _vel(80) _rndvel(20).

The sound out­put was played on a Pianoteq synthesizer: 

Trills

The fol­low­ing gram­mar pro­duces trills tak­ing advan­tage of tem­po vari­a­tions and con­tin­u­ous vari­a­tions of velocities:

Show grammar

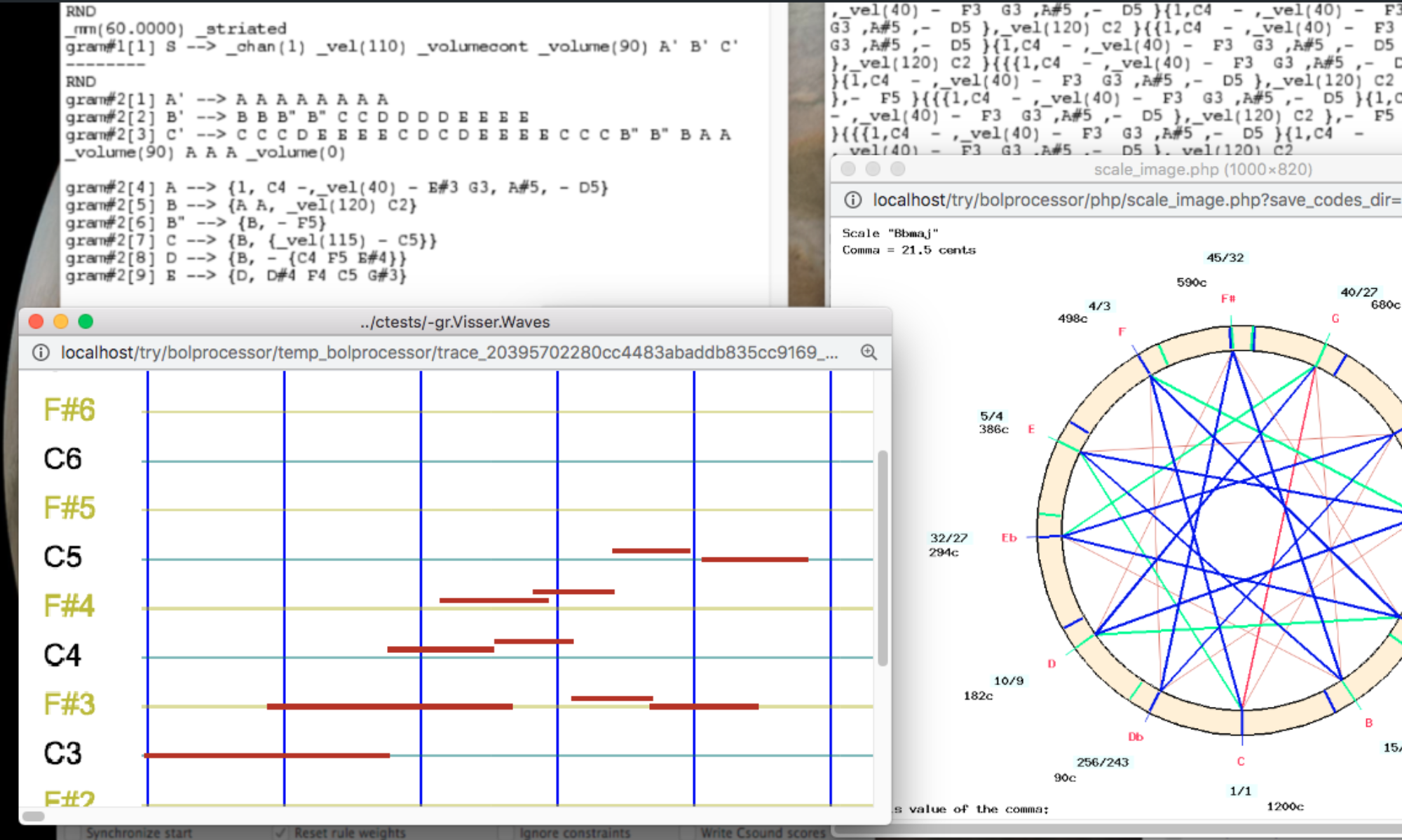
Waves

Harm Visser had been invit­ed to com­pose a piece à la Debussy with ruba­to rhythms cre­at­ing the impres­sion of wav­ing move­ments. We had expect­ed him to use the “_tempo()” tool with floating-point val­ues (or inte­ger ratios) as arguments.

In fact he did not… In the fol­low­ing gram­mar, only mark­ers “1/2”, “1/4” indi­cate reg­u­lar speed changes applied to an entire sec­tion. The wav­ing effect is pro­duced by a clever use of (self-imbedded) poly­met­ric expres­sions. As indi­cat­ed by the com­pos­er: “It is build on the idea of imbed­ding: {5, A B {3, A B {2, A B C D} C D} C D}.”

Show grammar

The fol­low­ing is a ren­der­ing of the piece for piano solo on a Pianoteq synthesizer:

In the final ver­sion, the com­pos­er assigned parts to a dif­fer­ent MIDI chan­nel con­trol­ling a physical-model syn­the­sized sax­o­phone (which he had designed on his own): 

Fractals

Harm Visser sent this gram­mar with the fol­low­ing com­men­tr (1998):

It is com­plete­ly based on a func­tion that I have made in PatchWork. Take 3 notes and take their inter­vals to trans­pose. The result is a kind of ‘auto­trans­pose’. You get a ‘frac­tal’ - the idea of the famous Von Koch-curve. The next step is mak­ing a recur­sive loop, so that you can set the lev­el of recur­sion. The num­ber of notes grows expo­nen­tial: 3 9 27 81 243 etc. Of course you can do the same with rhythm-values.
This gram­mar is a BP2-version of exact­ly the same idea. It has 4 recur­sion lev­els. (You might also say ‘depth’. It is in fact a ‘copy’ of the PW-function). That’s why S --> L4 (lev­el 4) (num­ber of notes 243).
The dif­fer­ence between BP2 and PW is that the func­tion in PW is fixed, which is not the case in BP2. I can easy make sub­tle changes (devi­a­tions) in the process. I can ‘break in’, so to speak. In his gram­mar I have set a com­ma between M10 and M11 and set M11 on the sax. The result is a poly­met­ric canon!

Show grammar

The fol­low­ing sound ren­der­ing is with piano solo on a Pianoteq syn­the­siz­er. The ver­sion with sax­o­phone is unfor­tu­nate­ly miss­ing. It could be gen­er­at­ed play­ing the (type-1) MIDI file Visser8.mid on a syn­the­siz­er assign­ing MIDI chan­nel 9 to a sax­o­phone sound.

References

• Time and Musical Structures (1990)
• Migrating Musical Concepts: An Overview of the Bol Processor (1998)