BP1 in its real musical context

In a pre­vi­ous arti­cle we explained how to install and run the Bol Processor ‘BP1’ on a vir­tu­al Apple IIe. BP1 is the ear­li­est ver­sion of Bol Processor imple­ment­ed on Apple II com­put­ers in 1981, as a require­ment for Jim Kippen’s field­work in India — see At the heart of Indian rhythms and their evo­lu­tion.… We will now show its oper­a­tion in a real musi­cal con­text: the mod­el­ling of a 'theme-and-variations' piece of drum­ming (called q‘aida) taught by Ustad Afaq Husain Khan, an expert in the Lucknow style of tabla in India.

This work dates back to the 1980s and has been doc­u­ment­ed in sev­er­al pub­li­ca­tions, includ­ing Kippen and Bel's Modelling music with gram­mars: for­mal lan­guage rep­re­sen­ta­tion in the Bol Processor (1992), from which the exam­ple will be tak­en. Extract (page 207):

A large part of the tabla reper­toire is impro­vi­sa­tion. Any sequence of strokes can be seen as a finite string of sym­bols whose organ­i­sa­tion is relat­ed to an implic­it for­mal sys­tem. Automatic sequences (i.e. sequences gen­er­at­ed by finite-state automa­ta) have prop­er­ties that place them some­where between peri­od­ic­i­ty and chaos, but clos­er to peri­od­ic­i­ty. Since both strict and approx­i­mate peri­od­ic­i­ty are essen­tial fea­tures of music, it is real­is­tic to think that sequences of musi­cal events can be ade­quate­ly rep­re­sent­ed by automa­ta or for­mal gram­mars. In oth­er words, the most fun­da­men­tal rea­son for us to con­sid­er for­mal lan­guage mod­els as rel­e­vant mod­els of music lies in prop­er­ties that are intrin­sic to music, rather than in ana­log­i­cal links between music and nat­ur­al languages.

The theme of this q‘aida is the fol­low­ing sequence:

dhatid­hage	nad­ha­trkt	dhatid­hage	dheena­ge­na
dhatid­hage	nad­ha­trkt	dhatid­hage	teenake­na
tati­take	nata­trkt	tati­take	teenake­na
dhatid­hage	nad­ha­trkt	dhatid­hage	dheena­ge­na

Strokes on the drum — bols like 'dha', 'ti', 'ge', 'na'… — belong to the (ter­mi­nal) alpha­bet of the for­mal gram­mar. This sequence should be read lin­ear­ly from left to right. Each group rep­re­sents a beat of 4 units ('trkt' is a com­pound stroke of 2 units). Thus, the theme and its vari­a­tions are framed on a 16-beat rhyth­mic mod­el called tin­tal in North-Indian music.

The gram­mar and exam­ples of this qa‘ida are stored as "Q2.7" on disc "BP-JULY87.DSK" which can be loaded after start­ing the Bol Processor (BP-PRG.DSK). We rec­om­mend that you set the vir­tu­al Apple II to max­i­mum speed to save time when read­ing (vir­tu­al) discs! After load­ing the Q2.7's gram­mar and data, the theme can be dis­played as data item #2:

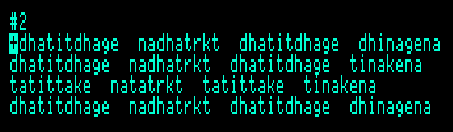
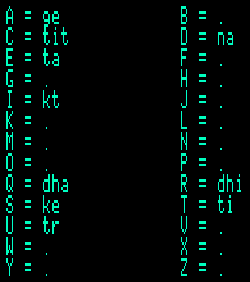
Note that the ter­mi­nal alpha­bet used on BP1 is not exact­ly the same as in the pub­li­ca­tion. For exam­ple, 'dhee' has been replaced by 'dhi', 'tee' by 'ti', sub­stan­tial changes for read­ers who pre­fer a translit­er­a­tion of Hindustani phonemes to the ren­der­ing of syl­la­bles in English.

In addi­tion, syl­la­ble 'ti' can be ren­dered as 'tit'. These sub­tleties are gov­erned by the key­board map­ping, which can be viewed (and mod­i­fied) by select­ing "Alphabet" then "Modify" from the main menu.

The gram­mar imple­ment­ed in BP1 is the same as that shown in Appendix 2 of the pub­li­ca­tion, except for spelling vari­ants of some bols and dif­fer­ent glyphs used to mark pat­terns - "mas­ter" and "slave" mark­ers, see our Pattern gram­mars arti­cle — and the bol den­si­ty instruc­tion, as explained in a pre­vi­ous arti­cle. For exam­ple, the rule

GRAM#2 [20] <100>  S32  <—>  * (= /6+ A16  V8 + /4) + O16

was dis­played as:

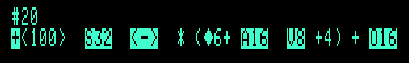
The bol den­si­ty mark­er "6" is now writ­ten as "/6" and "4" as "/4". The plus sign '+' is used as a con­text marker.

In lat­er ver­sions of the Bol Processor, we cre­at­ed a "_tempo()" tool which is more flex­i­ble than bol den­si­ty. For exam­ple, "_tempo(8)" would have the same effect as "/8" in a sim­ple sequence. However, in poly­phon­ic struc­tures, "/8" is an absolute val­ue where­as "_tempo(8)" is rel­a­tive to the cur­rent tem­po. This makes it pos­si­ble to cal­i­brate the dura­tions of sev­er­al sequences con­tained in a poly­met­ric expres­sion — see Two Algorithms for the Instantiation of Musical Structures (1994) for details. Furthermore, expres­sions such as "_tempo(7/4)" and even "_tempo(0.476)" are permitted…

Templates

Subrammar #7 con­tains the tem­plates of this grammar:

[1]   TEM
[2]   (=+.….….….…+.….….….…+ * (=+.….….….…+) +.….….….…;)
[3]   (=+.….….….…+.….….….…+ * (=+.….….….…+) +/8+.….….….….….….….…;/4;)
[4]   (=+.….….….…+.….….….…+ * (=/6+.….….…/4.….…+) +.….….….…;)
etc.

These tem­plates are the com­plete list of pat­terns pro­duced by (pre­sum­ably) all vari­a­tions of the q‘aida. They con­tain paren­the­ses sur­round­ing ref­er­ence strings with the "=" mark­er (dis­played as "◆" in BP1), bol den­si­ty num­bers, and arbi­trary "+" and ";" sym­bols used as con­text in the rule, as explained in the pub­li­ca­tion. Technically, pat­terns are sim­i­lar to reg­u­lar expres­sions against which a vari­a­tion is checked before being parsed by the grammar.

Any gram­mar that con­tains pat­terns and/or bol den­si­ty fig­ures must be sup­ple­ment­ed with tem­plates in order to assess the gram­mat­i­cal­i­ty of vari­a­tions. Fortunately, these tem­plates are auto­mat­i­cal­ly gen­er­at­ed by the grammar!

Producing items

To cre­ate vari­a­tions based on this gram­mar, select "Grammars" from the main menu, then go to sub­gram­mar #1, "Edit", and move to rule #2, for example:

<100>  S  <—>  (=+ S64 ;)

This will pro­duce vari­a­tions of 64 bols as sug­gest­ed by the name of the vari­able "S64". Rule #3 would pro­duce vari­a­tions of 128 bols as sug­gest­ed by "D128".

Type ctrl-C ([C]ompute). You will be asked to spec­i­fy the first sub­gram­mar (1) and the last sub­gram­mar (6). For exam­ple, if you are start­ing to com­pute from a rule of sub­gram­mar #3, it makes sense to spec­i­fy #3 as the first sub­gram­mar. If a sub­gram­mar low­er than 6 is spec­i­fied as the last, some vari­ables may not be rewrit­ten as strings of ter­mi­nal sym­bols. This can be use­ful for check­ing sub-processes in the pro­duc­tion of variations.

The options offered are A)nalyse, S)ynthesize, D)estroy struc­ture and Q)uit. Select "Synthesize". Say 'no' to "Create tem­plates" and "Systematic tree-search". You may answer 'yes' to "Step by step?" to see all the deriva­tion steps, so you can famil­iarise your­self with the gram­mar. Example of a result:

This is an inter­est­ing exam­ple: in the third line, the bol den­si­ty is dou­bled (8 instead of 4).

You are now offered the option to "Append" the vari­a­tion to the data set, "Repeat" the pro­duc­tion process, "Print" (on the vir­tu­al print­er), cre­ate "More" vari­a­tions or "Verify" this vari­a­tion. It is not obvi­ous that the gram­mar will accept this vari­a­tion if it is poor­ly designed. (This is unlike­ly in this exam­ple.) The "Verify" option should quick­ly end up with "S", the start string, if the vari­a­tion is correct.

If some vari­a­tions have been added to the data set, edit­ing Data will dis­play them at the end of the set.

This process of pro­duc­ing vari­a­tions is called "modus ponens" in expert sys­tems jar­gon. Variations pro­duced in this way were read by the ana­lyst (Jim Kippen) to the expert musi­cian to check their accep­tance as legit­i­mate vari­a­tions of the q‘aida.

Analyzing variations

Now imag­ine the expert musi­cian play­ing a vari­a­tion that is typed into the data set. It is clear that fast and accu­rate typ­ing was cru­cial to this field research… Use key­board map­ping to learn to type at high speed; it is less dif­fi­cult than play­ing the drums!

When a vari­a­tion is dis­played in the data set, type ctrl-C for "[C]ompute". Answer 'yes' to "Revise pro­cess­ing?". Now the first gram­mar is #1 but the last gram­mar should be #7 so that tem­plates are tak­en into account. Select "Analyse", say 'no' to "Display prob­a­bil­i­ty?" and 'yes' or 'no' to "Step by step?".

If you are analysing step by step, use the right arrow to go for­ward or the left arrow to go back. The sub­gram­mar cur­rent­ly used for deriva­tions is shown at the bot­tom of the page, and the index of the lat­est can­di­date rule appears at the top. In this way it is pos­si­ble to visu­alise all the details of the cal­cu­la­tion for the pro­duc­tion or analy­sis of a variation.

You can check the entire data set against the gram­mar by select­ing "Verify gram­mars" from the main menu.

If the vari­a­tion match­es more than one tem­plate, each tem­plate is used to parse it. If the pars­ing is suc­cess­ful with mul­ti­ple tem­plates, the struc­ture of the piece is ambigu­ous. This is anal­o­gous to pars­ing the sen­tence "Mary said John is a liar", which requires the place­ment of either two com­mas or a semi­colon, with each "tem­plate" giv­ing an oppo­site meaning…

Weights

Currently, in the gram­mar, all rule weights are set to 100 except for rule #3 of sub­gram­mar #1. We can use the 12 vari­a­tions in the data set to infer rule weights: each of them is analysed and each rule has its weight increased by 1 unit.

Select "Weights" from the main menu, then "Emulate learn­ing" and "Reset weights to 0". From item #2 to item #13. The last gram­mar is "7" (as tem­plates are required).

The result can be print­ed. Note that all weights in sub­gram­mar #6 are set to 100 because it is an "ORD" gram­mar: no ran­dom selec­tion of the can­di­date rule.

The input of new data sets allowed "learn­ing" from more exam­ples and improv­ing the sto­chas­tic mod­el, which would pro­duce more "aes­thet­i­cal­ly accept­able" variations.

Intermediate alphabet

Accessed from the main menu. This pro­ce­dure is used to chang­ie the names of vari­ables. This pro­ce­dure has proved use­ful in cre­at­ing gram­mars that make sense to humans, not just machines…

Creating templates

To check this, it is rec­om­mend­ed to quit and reload the cur­rent project, as some pro­ce­dures may have been saved in mem­o­ry. Load only the gram­mar, no data, to keep enough free memory.

Select "Grammars" from the main menu, then go to sub­gram­mar #7 (the cur­rent tem­plates) and delete it by select­ing "Remove from series". (This may not be nec­es­sary as the machine nev­er dupli­cates a tem­plate, but it makes things clearer.)

Then cre­ate a new sub­gram­mar #7, select "Compute" and "Create tem­plates". You will be asked for the "last gram­mar defin­ing struc­tures". This choice is very impor­tant for the speed of the com­pu­ta­tion, because the pro­duc­tion of tem­plates implies the pro­duc­tion of "all vari­a­tions". If your answer is "6", the machine can work extreme­ly long. Looking at the gram­mar, we can see that sub­gram­mar 3 is the last to con­tain struc­tur­al mark­ers. So the cor­rect answer is "3".

This process takes a long time, even at the high­est speed. Its progress is indi­cat­ed by '+' signs print­ed on the line below 'WAIT'. Since this gram­mar pro­duces 21 tem­plates, you have to wait for 21 '+' signs. Fortunately, in most gram­mars, the gen­er­a­tion of tem­plates is done once and for all…

Conclusion

This demo is an attempt to illus­trate the use of the Bol Processor BP1 in the ear­ly 1980s as an expert sys­tem for mod­el­ling compositional/improvisational process­es in the q‘aida genre of tabla drum­ming. Of great impor­tance was the devel­op­ment of an edi­tor that facil­i­tat­ed the rapid and accu­rate writ­ing of bols (rep­re­sen­ta­tions of drum strokes) and the cre­ation of pat­tern rules that took into account the implic­it syn­tac­tic struc­tures of these musi­cal pieces.

Later, the Bol proces­sor was imple­ment­ed on Macintosh com­put­ers. Versions of 'BP2' com­pat­i­ble with sys­tem ver­sions up to MacOS 10.14 (Mojave) can be dowloaded from SourceForge.

BP2 repro­duces all the pro­ce­dures of BP1, in par­tic­u­lar those described in Kippen & Bel's paper Modelling music with gram­mars: for­mal lan­guage rep­re­sen­ta­tion in the Bol Processor (1992). However, its edi­tor is not as sophis­ti­cat­ed in terms of pat­tern edit­ing. Also, the "smart key­board" option allows ter­mi­nal sym­bols to be mapped to indi­vid­ual keys, but the cur­sor does not "jump" over ter­mi­nal sym­bols, vari­ables and reserved words.

BP2 intro­duced the pos­si­bil­i­ty of polyphonic/polyrhythmic rep­re­sen­ta­tion. Polymetric struc­tures are an unsur­passed mod­el for rep­re­sent­ing musi­cal time and, by exten­sion, the struc­ture of "time objects": music, speech, noise, video, robot move­ments, etc. This mod­el is able to deal with incom­plete def­i­n­i­tions and per­forms all ter­mi­nal time cal­cu­la­tions accu­rate­ly, using inte­ger ratios. The results are sim­pli­fied to avoid inte­ger over­flow and to match the quan­ti­za­tion required for real performance.

Current work

A new ver­sion of Bol Processor com­pat­i­ble with 64-bit proces­sors on var­i­ous sys­tems (MacOS, Windows, Linux…) is cur­rent­ly under devel­op­ment. It works with a PHP/JavaScript inter­face. We invite soft­ware design­ers to join the team and con­tribute to the devel­op­ment of the core appli­ca­tion and its client appli­ca­tions. Please join the BP open dis­cus­sion forum and/or the BP devel­op­ers list to stay in touch with the progress of the work progress and to dis­cuss relat­ed the­o­ret­i­cal issues.

References

• Time and Musical Structures (1990) on poly­met­ric structures
• Two Algorithms for the Instantiation of Musical Structures (1994) on poly­met­ric struc­tures and the time-setting algo­rithm of sound objects
• Migrating Musical Concepts: An Overview of the Bol Processor (1998) for a gen­er­al pre­sen­ta­tion includ­ing a descrip­tion of quan­ti­za­tion.

---

Contributors to this arti­cle: Bernard Bel