A Mathematical Discussion of the Ancient Theory of Scales according to Natyashastra

Bernard Bel

Note interne, Groupe Représentation et Traitement des Connaissances (CNRS), Marseille 1988.

👉  Cited on page The two-vina experiment

Résumé

Le Natyashastra, un traité san­scrit sur la musique, la danse et le théa­tre, con­tient une théorie des échelles musi­cales qui sert de base à la clas­si­fi­ca­tion de formes mélodiques. De nom­breux auteurs indi­ens et occi­den­taux ont pro­posé des inter­pré­ta­tions de cette théorie, et plus récem­ment des travaux ont été menés pour valid­er ces inter­pré­ta­tions à par­tir de don­nées acous­tiques tirées de la pra­tique musi­cale en Inde. Cet arti­cle énonce les raisons pour lesquelles une telle val­i­da­tion n'est pas pos­si­ble, et pro­pose une inter­pré­ta­tion générale de la théorie s'appuyant sur la réso­lu­tion de sys­tèmes d'équations linéaires. Les sys­tèmes déduits des prémiss­es ont un degré d'indétermination. Les ensem­bles solu­tions cor­re­spon­dent à divers­es hypothès­es per­me­t­tant de lever l'indétermination, ten­ant compte de con­sid­éra­tions acous­tiques cor­re­spon­dant à divers­es con­cep­tions musi­cales: tem­péra­ment, into­na­tion juste, etc.

Excerpts of an AI review of this paper (Academia, June 2025)

Summary

This paper offers a detailed math­e­mat­i­cal explo­ration of the scale the­o­ry described in Bharata’s Natyashastra, focus­ing par­tic­u­lar­ly on the con­cept of 22 shrutis (microin­t­er­vals) that con­sti­tute var­i­ous Indian musi­cal scales. It encom­pass­es his­tor­i­cal con­text, the­o­ret­i­cal deriva­tions of inter­val sizes, and poten­tial tun­ing con­fig­u­ra­tions. The author com­bines tex­tu­al evi­dence from ancient Sanskrit sources (espe­cial­ly the first six chap­ters of the Natyashastra) with alge­bra­ic meth­ods to pro­pose both tem­pered and just-intonation sys­tems con­sis­tent with Bharata’s frame­work. Experimental ref­er­ences — such as mono­chord exper­i­ments, work with an elec­tron­ic Shruti Harmonium, and Melodic Movement Analyser (MMA) analy­ses — are includ­ed to con­nect the­o­ret­i­cal pos­si­bil­i­ties with prac­ti­cal musi­cal performance.

Organization & Clarity

Historical Introduction and Context

• The paper begins by sit­u­at­ing Bharata’s Natyashastra with­in the con­tin­u­um of Indian music the­o­ry, ref­er­enc­ing key fig­ures and exper­i­ments from both Indian and Western traditions.
• This his­tor­i­cal back­ground sets the stage for the dis­cus­sion, although in places it could be stream­lined to high­light the cen­tral premise of the math­e­mat­i­cal framework.

Algebraic Formulation

• The author sys­tem­at­i­cal­ly trans­lates Bharata’s tex­tu­al state­ments into sets of alge­bra­ic equations.
• The tran­si­tion from tex­tu­al asser­tions (e.g., “SP2 = 13 shruti-s”) to equa­tions in cents is pre­sent­ed step by step, aid­ing clarity.

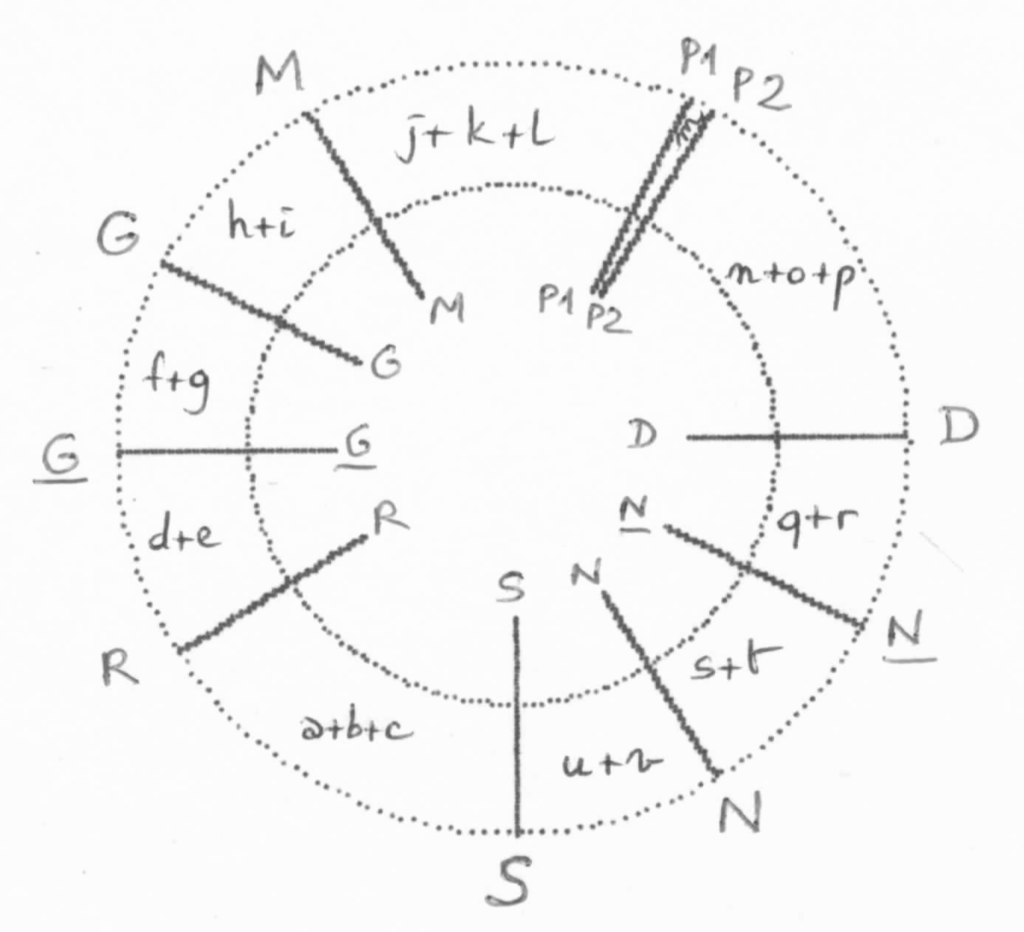
Figures and Tables

• The paper fre­quent­ly ref­er­ences fig­ures (e.g., “fig 1”, “fig 2”, etc.) and tables of coef­fi­cients result­ing from these equations.
• These graph­i­cal or tab­u­lar rep­re­sen­ta­tions appear to play a crit­i­cal role in help­ing read­ers visu­al­ize rela­tion­ships but would ben­e­fit from clear­er ref­er­ences and label­ing to make them more accessible.

Overall, the con­tent is laid out in a sequen­tial man­ner, mov­ing from ancient the­o­ry to alge­bra­ic method, then to spe­cif­ic tun­ing sys­tems, and final­ly to pos­si­ble applications.

Technical & Theoretical Contributions

Translating Ancient Theories into Modern Frameworks

• The paper bridges tra­di­tion­al Indian music the­o­ry with mod­ern math­e­mat­i­cal nota­tion, a valu­able approach that can expand under­stand­ing for researchers from vary­ing backgrounds.
• The dis­tinc­tion made between “topo­log­i­cal” rela­tion­ships (i.e., how inter­vals add up) and actu­al fre­quen­cy ratios is cru­cial, and the paper address­es poten­tial pit­falls in pre­sum­ing a sin­gle “cor­rect” interpretation.

Multiple Tuning Scenarios

• The author explores a range of tun­ing pro­ce­dures (e.g., har­mon­ic major third vs. Pythagorean major third) and com­pares their outcomes.
• The paper shows how vari­a­tions in the pra­mana shru­ti (the “one-shruti” unit) can pro­duce marked­ly dif­fer­ent yet the­o­ret­i­cal­ly valid scales.

Focus on Consonance and System Consistency

• By impos­ing con­straints of mur­ccha­na (shift­ing ton­ics), the paper demon­strates how the 22 micro­tones can remain inter­nal­ly consistent.
• The deriva­tion of tem­pered and just-intonation vari­ants helps illus­trate how “ancient” the­o­ry can align with cur­rent the­o­ret­i­cal con­cepts such as com­mas, semi­tones, and limmas.

Methodological Rigor

Logical Steps of Equation Building

The paper method­i­cal­ly shows how each note rela­tion­ship leads to an equa­tion or inequal­i­ty. This approach is clear, though some dense sec­tions (espe­cial­ly when list­ing large sets of equa­tions) may chal­lenge read­ers less accus­tomed to math­e­mat­i­cal proofs.

Scope and Assumptions

The paper acknowl­edges an impor­tant assump­tion: that ancient tex­tu­al descrip­tions can be faith­ful­ly trans­posed into alge­bra­ic rela­tion­ships. This is nec­es­sary but might ben­e­fit from more explic­it caveats about inter­pre­ta­tion­al breadth in his­tor­i­cal musi­col­o­gy (e.g., vari­a­tions in tex­tu­al trans­mis­sion, poten­tial scrib­al changes, etc.).

Use of Empirical Data

Empirical ref­er­ences to tun­ing exper­i­ments (e.g., on the Shruti Harmonium) com­ple­ment the the­o­ret­i­cal work. Future expan­sions could include more detail on the data col­lec­tion and sta­tis­ti­cal analy­sis, if applicable.

Strengths

• Clearly ground­ed in both his­tor­i­cal tex­tu­al sources and mod­ern math­e­mat­i­cal treatments.
• Provides mul­ti­ple path­ways (tem­pered vs. just) and high­lights how each main­tains inter­nal con­sis­ten­cy per Bharata’s intervals.
• Shows ver­sa­til­i­ty in micro­ton­al arith­metic, illus­trat­ing that mul­ti­ple valid inter­pre­ta­tions exist instead of a sin­gle, fixed approach.

Overall, this paper illu­mi­nates the com­plex­i­ty and depth of Bharata’s scale the­o­ry by mar­ry­ing philo­log­i­cal analy­sis with alge­bra­ic pre­ci­sion. The dis­cus­sion of how these ancient con­cepts can pro­duce wide-ranging, inter­nal­ly con­sis­tent tun­ing sys­tems con­tributes sub­stan­tial­ly to eth­no­mu­si­col­o­gy, Indian music schol­ar­ship, and broad­er micro­ton­al research.

Download this paper