A Mathematical Model of the Shruti-Swara-Grama-Murcchana-Jati System

E. James Arnold

Journal of the Sangit Natak Akademi, New Delhi 1982.

👉  Cited on page The two-vina experiment

Abstract

The first sec­tion of this paper con­sid­ers the math­e­mat­i­cal and musi­cal prin­ci­ples by which the shru­ti posi­tions (note posi­tions in the sys­tem of "just into­na­tion") are deter­mined. A sys­tem of short­hand tun­ing sym­bols is giv­en by which the tun­ing pro­ce­dures for each of the shru­ti posi­tions is con­cise­ly expressed. Using these sym­bols to sum­ma­rize the appro­pri­ate tun­ing pro­ce­dures, the posi­tions of the shrutis are giv­en in tables of families.

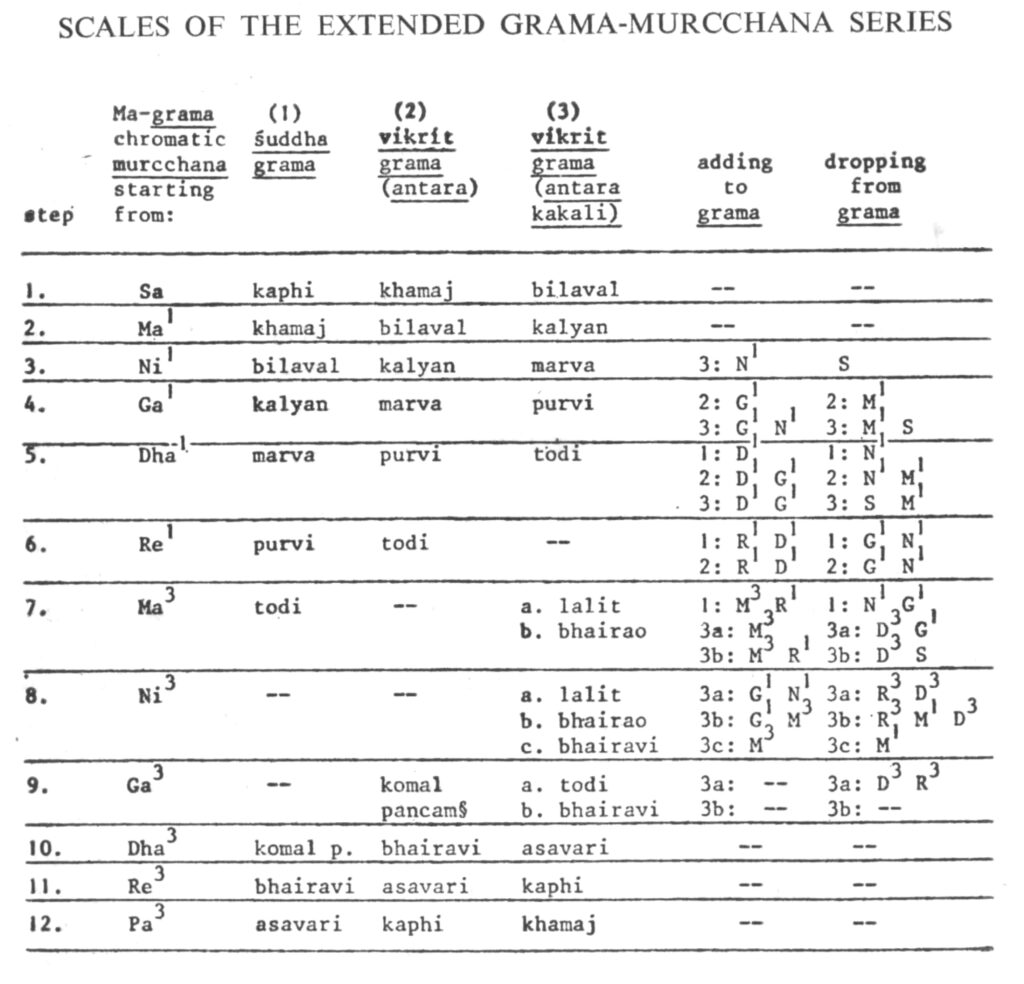
Then fol­lows a descrip­tion of a sim­ple math­e­mat­i­cal mod­el of the shruti-swara-grama-murchana sys­tem of Bharata, Dattila, and Sharangadeva. A study of the har­mon­ic struc­ture of the gra­mas (fun­da­men­tal scales) reveals that the prin­ci­ple scale-types employed in Hindustani clas­si­cal music form a 'main-sequence' of scales direct­ly relat­able to the har­mon­ic struc­ture of the ancient gra­mas. This is sum­ma­rized in a table of the 'extend­ed mur­chana series' of scales deriv­able from the Ma and Sa gra­mas.

Excerpts of an AI review of this paper (Academia, June 2025)

This paper presents a rig­or­ous math­e­mat­i­cal frame­work for under­stand­ing one of the most com­plex and foun­da­tion­al con­cepts in Indian clas­si­cal music the­o­ry: the ancient sys­tem of shrutis (micro­ton­al inter­vals) and their rela­tion­ship to scales (gra­mas) and melod­ic types (jatis). Arnold's work bridges the gap between abstract musi­co­log­i­cal the­o­ry and prac­ti­cal appli­ca­tion through inno­v­a­tive math­e­mat­i­cal mod­el­ing and visu­al representation.

Theoretical Foundation and Methodology

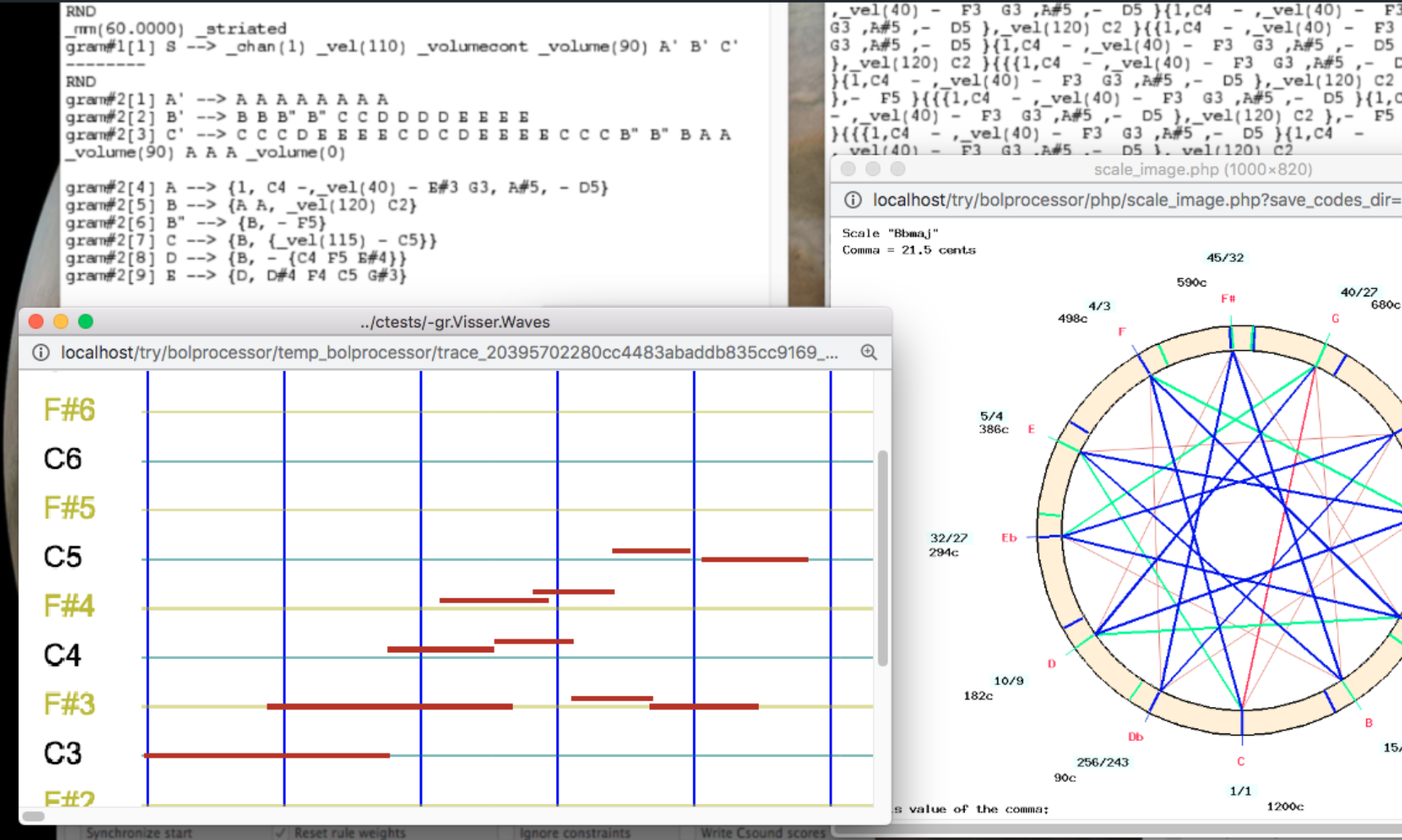
Arnold begins by address­ing a fun­da­men­tal chal­lenge in Indian music the­o­ry: the pre­cise deter­mi­na­tion of shru­ti posi­tions with­in the octave. The tra­di­tion­al sys­tem rec­og­nizes 22 shrutis as the basic build­ing blocks of melody, but their exact tun­ing has remained con­tentious among schol­ars and prac­ti­tion­ers. The author devel­ops an ele­gant short­hand nota­tion sys­tem that con­cise­ly express­es tun­ing pro­ce­dures for each shru­ti posi­tion, mak­ing com­plex inter­val­lic rela­tion­ships acces­si­ble through sym­bol­ic representation.

The paper's math­e­mat­i­cal approach is ground­ed in just into­na­tion prin­ci­ples, using fre­quen­cy ratios derived from the har­mon­ic series. Arnold sys­tem­at­i­cal­ly works through the math­e­mat­i­cal rela­tion­ships that define each shru­ti, pre­sent­ing detailed tables that show the fre­quen­cy ratios, peri­ods, and har­mon­ic rela­tion­ships for dif­fer­ent fam­i­lies of shru­ti posi­tions. This method­i­cal approach pro­vides unprece­dent­ed clar­i­ty to what has his­tor­i­cal­ly been a murky area of music theory.

The Physical Model

One of the paper's most inno­v­a­tive con­tri­bu­tions is the descrip­tion of a phys­i­cal mod­el con­sist­ing of two rotat­ing wheels: a fixed out­er wheel rep­re­sent­ing shru­ti divi­sions and a mov­able inner wheel rep­re­sent­ing gra­ma scales. This tan­gi­ble device allows musi­cians and the­o­rists to visu­al­ize the com­plex rela­tion­ships between dif­fer­ent scale types and their har­mon­ic impli­ca­tions. The mod­el serves as both an ana­lyt­i­cal tool and a prac­ti­cal cal­cu­la­tor for deter­min­ing inter­val­lic rela­tion­ships between any two shru­ti positions.

The wheel design reflects deep under­stand­ing of the cycli­cal nature of musi­cal inter­vals and demon­strates how ancient Indian the­o­rists like Bharata, Dattila, and Sharangadeva con­cep­tu­al­ized har­mon­ic rela­tion­ships. By mak­ing these abstract con­cepts phys­i­cal­ly manip­u­la­ble, Arnold pro­vides an invalu­able ped­a­gog­i­cal tool for under­stand­ing clas­si­cal Indian music theory.

Historical Integration and Validation

Arnold val­i­dates his math­e­mat­i­cal mod­el against the writ­ings of ancient the­o­rists, par­tic­u­lar­ly focus­ing on the grama-murchana sys­tem described in clas­si­cal trea­tis­es. The paper demon­strates how the prin­ci­ple scale-types used in con­tem­po­rary Hindustani clas­si­cal music can be traced back to these ancient har­mon­ic struc­tures, form­ing what Arnold terms a "main-sequence" of scales direct­ly relat­ed to the fun­da­men­tal gra­mas.

This his­tor­i­cal ground­ing lends cred­i­bil­i­ty to the math­e­mat­i­cal frame­work while simul­ta­ne­ous­ly pro­vid­ing new insights into the evo­lu­tion of Indian musi­cal prac­tice. The paper shows how mod­ern ragas main­tain har­mon­ic rela­tion­ships with their ancient pre­de­ces­sors, despite cen­turies of styl­is­tic development.

Practical Applications and Limitations

The model's prac­ti­cal util­i­ty extends beyond the­o­ret­i­cal analy­sis to per­for­mance appli­ca­tions. Arnold sug­gests the sys­tem can help deter­mine inter­val rela­tion­ships, study melod­ic move­ment in ragas, and under­stand har­mon­ic con­so­nance pat­terns. However, the paper acknowl­edges impor­tant lim­i­ta­tions, par­tic­u­lar­ly not­ing that actu­al per­for­mance prac­tice in Indian clas­si­cal music involves con­stant micro­ton­al adjust­ments rather than fixed fre­quen­cy relationships.

This recog­ni­tion of the dif­fer­ence between the­o­ret­i­cal mod­els and liv­ing musi­cal prac­tice demon­strates Arnold's nuanced under­stand­ing of Indian music. The author appro­pri­ate­ly posi­tions the math­e­mat­i­cal frame­work as a tool for under­stand­ing struc­tur­al prin­ci­ples rather than a pre­scrip­tion for per­for­mance practice.

Significance and Impact

Arnold's work rep­re­sents a sig­nif­i­cant con­tri­bu­tion to eth­no­mu­si­col­o­gy and music the­o­ry, pro­vid­ing the first com­pre­hen­sive math­e­mat­i­cal mod­el of the ancient Indian tonal sys­tem. The paper suc­cess­ful­ly demon­strates that rig­or­ous ana­lyt­i­cal meth­ods can illu­mi­nate tra­di­tion­al music sys­tems with­out dimin­ish­ing their cul­tur­al authen­tic­i­ty or prac­ti­cal flexibility.

The inte­gra­tion of his­tor­i­cal schol­ar­ship, math­e­mat­i­cal analy­sis, and prac­ti­cal appli­ca­tion makes this work valu­able for mul­ti­ple audi­ences: music the­o­rists seek­ing ana­lyt­i­cal frame­works, per­form­ers want­i­ng deep­er under­stand­ing of raga struc­ture, and schol­ars of Indian cul­ture explor­ing the math­e­mat­i­cal sophis­ti­ca­tion of clas­si­cal treatises.

While the paper's tech­ni­cal nature may lim­it its acces­si­bil­i­ty to gen­er­al read­ers, its method­olog­i­cal inno­va­tions and the­o­ret­i­cal insights estab­lish it as essen­tial read­ing for any­one seri­ous­ly engaged with Indian clas­si­cal music the­o­ry or com­par­a­tive musicology.

Download this paper