Timebase to polymetric

This algo­rithm is used by the PHP inter­face of Bol Processor ‘BP3’ under devel­op­ment. Read:

https://bolprocessor.org/misc/BP3/CheckList.html#timebase

It is imple­ment­ed in func­tion polymetric_expression() of file _basic_tasks.php (read below).

The func­tion cre­ates a poly­met­ric expres­sion equiv­a­lent to the rhyth­mic struc­ture pro­grammed on a Timebase page. We will take for instance a struc­ture which does not sound musi­cal because of its odd ratios:

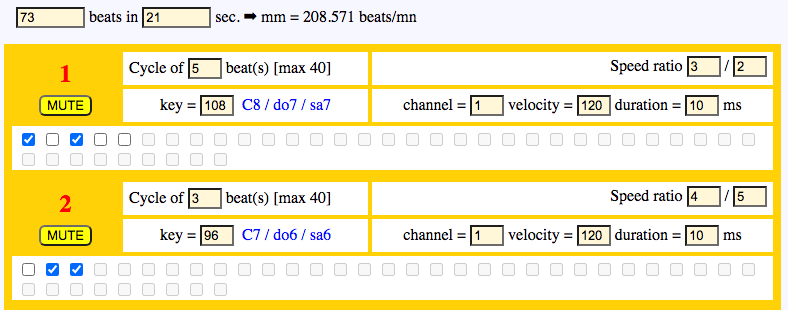
The metronome speed is 208.571 beats per minute spec­i­fied as 73 beats in 21 sec­onds. Bol Processor always com­pute dura­tions as inte­ger ratios.

Let us define p_clock = 73 and q_clock = 21.

This struc­ture con­tains 2 tracks. The fol­low­ing algo­rithm deals with any num­ber of tracks.

• Track 1 is a cycle of 5 beats [TickCycle] and its speed ratio is 3/2 [Ptick/Qtick]. It pro­duces note C8 (in English nota­tion) at veloc­i­ty 120 (a MIDI para­me­ter) and dura­tion 10 mil­lisec­onds.
• Track 2 is a cycle of 3 beats [TickCycle] and its speed ratio is 4/5 [Ptick/Qtick]. It pro­duces note C7 at veloc­i­ty 120 and dura­tion 10 mil­lisec­onds.

Tick cycles are made explic­it by checked/unchecked box­es. Unchecked box­es denote silences ‘-’:

• C8 - C8 - - for the first track
• - C7 C7 for the sec­ond track

The rhyth­mic struc­ture will be rep­re­sent­ed as a poly­met­ric struc­ture with 2 fields {Track1, Track2} in which fields are forced to the same sym­bol­ic dura­tion by the poly­met­ric expan­sion algo­rithm (described here). We need to design its con­tent so that the expan­sion does not alter the tem­po declared on each track.

To this effect, con­sid­er the sym­bol­ic dura­tion of each track:

(q_clock / p_clock) * (TickCycle * Qtick) / Ptick

In order to match sym­bol­ic dura­tions, each track should be repeat­ed adequately:

repeat1 * (TickCycle1 * Qtick1) / Ptick1 = repeat2 * (TickCycle2 * Qtick2) / Ptick2 = …

Ratio (q_clock / p_clock) being iden­ti­cal for each track
was elim­i­nat­ed from this equation.

We need to find the set of small­est inte­gers repeat1, repeat2 etc. sat­is­fy­ing this equation.

To this effect, we sim­pli­fy ratio (TickCycle * Qtick) / Ptick using the great­est com­mon divi­sor (GCD):

x = GCD((TickCycle * Qtick), Ptick)
y = (TickCycle * Qtick) / x

Then we cal­cu­late the least com­mon mul­ti­ple (LCM) of all y values:

lcm = LCM(y1, y2, …)

This yields for each field:

repeat = (lcm * Ptick) / (TickCycle * Qtick)

In prac­tice,

x1 = GCD((TickCycle1 * Qtick1), Ptick1) = GCD((5 * 2), 3) = 1
y1 = (TickCycle1 * Qtick1) / x1 = (5 * 2) / 1 = 10

x2 = GCD((TickCycle2 * Qtick2), Ptick2) = GCD((3 * 5), 4) = 1
y2 = (TickCycle2 * Qtick2) / x2 = (3 * 5) / 1 = 15

lcm = LCM(10,15) = 30

repeat1 = (lcm * Ptick1) / (TickCycle1 * Qtick1) = (30 * 3) / (5 * 2) = 9
repeat2 = (lcm * Ptick2) / (TickCycle2 * Qtick2) = (30 * 4) / (3 * 5) = 8

The struc­ture will there­fore look like:

{Track1 Track1 Track1 Track1 Track1 Track1 Track1 Track1 Track1, Track2 Track2 Track2 Track2 Track2 Track2 Track2 Track2}

We need to include per­for­mance para­me­ters set­ting the dura­tion of ticks. To this effect, we use the _staccato(s) para­me­ter in which s is the per­cent­age of cropped dura­tion at the end of the sound-event. Durations have been set to 10 mil­lisec­onds. We cal­cu­late the peri­od of each track:

period1 = (((1000 * q_clock) / p_clock) * Qtick1) / Ptick1 = (((1000 * 21) / 73) * 2) / 3 = 192 ms
s1 = 100 * (192 - 10) / 192 = 94%
period2 = (((1000 * q_clock) / p_clock) * Qtick2) / Ptick2 = (((1000 * 21) / 73) * 5) / 4 = 359 ms
s2 = 100 * (359 - 10) / 359 = 97%

Finally, we spec­i­fy the tem­po of each field: 3/2 for the first one and 4/5 for the sec­ond one.

The result­ing poly­met­ric struc­ture is:

{_tempo(3/2) _chan(1) _vel(120) _staccato(94) C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - , _tempo(4/5) _chan(1) _vel(120) _staccato(97) - C7 C7 - C7 C7 - C7 C7 - C7 C7 - C7 C7 - C7 C7 - C7 C7 - C7 C7}

Note that _tempo(4/5) does not need to be spec­i­fied because it will be infered by the poly­met­ric expan­sion algo­rithm. Therefore, the expres­sion dis­played at the bot­tom of the Timebase page is:

{_tempo(3/2) _chan(1) _vel(120) _staccato(94) C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - C8 - C8 - - , _chan(1) _vel(120) _staccato(97) - C7 C7 - C7 C7 - C7 C7 - C7 C7 - C7 C7 - C7 C7 - C7 C7 - C7 C7}

Implementation in PHP

The fol­low­ing is the code in file _basic_tasks.php.

Table $mute con­tains flags indi­cat­ing whether a track is active or mute. Function key_to_note() returns the name of a note in English con­ven­tion giv­en its key num­ber (MIDI).