This page is intended for developers of the Bol Processor BP3 (read installation). It is not a formal description of the algorithms carried by the console's C code, but rather an illustration of their management of musical processes, which may be useful for checking or extending algorithms.
The title of this page should be "Tied sound objects" because sound objects can be tied in the same way as simple notes. However, it is more straightforward to demonstrate the process using simple notes.
All examples are included in the "ctests" folder of the distribution. A set of correct and incorrect examples is found in the "-da.checkTies" project.
Example of tied notes
Consider measures #18 to #22 of Liszt's 14th Hungarian Rhapsody imported from a MusicXML file — see Importing MusicXML scores. The printed score of measures #19 to #21 is as follows:


Source: ManWithNoName in the MuseScore community
Tied notes are visible on this score. Slurs connecting notes at different pitches are ignored by the Bol Processor. These could be interpreted using the _legato(x) performance control, but setting an appropriate value for 'x' would require a careful analysis of the context. Ties link the same pitch, such as "Ab1" (A flat in octave 1) at the bottom of the score lines. There are 3 occurrences of tied "Ab1" in this section, the first one starting at the end of measure #18 and the third one ending at measure #21.
In Bol Processor notation (also called polymetric notation), this fragment results in a sequence of polymetric structures. For the sake of clarity, each measure has been placed on its own paragraph:
#18 {_tempo(4/3) {4,{7/4,C4,C5}{1/4,C4,F4,Ab4,C5}{7/4,C4,F4,Ab4,C5}{1/4,Db4,F4,Ab4,Db5},{7/4,G4,Bb4}9/4,{7/4,E2,C3,G3,Bb3}{1/4,F2}{7/4,C3,F3,Ab3}{1/4, Ab1&}}
#19 {_tempo(4/3) {4,{15/4,Db4,F4,Ab4,Db5}1/8{1/8,C4,Gb4,B4,Eb5},{3/4,Ab2}{3,Db3 F3 Ab3 Db4 F4 Ab4 Db5 F5 Ab5 Db6 F6 Ab6}{1/4,- Ab1&}, &Ab1 ---}
#20 {_tempo(13/10) {33/8,{1/4,Db4& Gb4& A4& Eb5&}{7/2,&Db4,&Gb4,&A4,&Eb5}1/4{1/8,Fb4,Ab4,Cb5,Fb5},{3/4,Ab2}{13/4,Eb3 Gb3 A3 C4 G4 Bb4 Eb5 Gb5 A5 Eb6 Gb6 B6 -}{1/8, Ab1&}, &Ab1 25/8}}
#21 {_tempo(13/10) {33/8,{15/4,Fb4,Ab4,C5,Fb5}1/4{1/8,F4,Ab4,Db5,F5},{3/4,Ab2}{13/4,Fb3 Ab3 Cb4 F4 Ab4 C5 F5 Ab5 Cb6 Fb6 Ab6 Cb7 -}{1/8,B1&}, &Ab1 25/8}}
#22 {_tempo(4/3) {4,{7/2,F4,Ab4,Db5,F5}1/2,{3/4,B2}{13/4,F3 Ab3 Db4 F4 Ab4 Db5 F5 Ab5 Db6 F6 Ab6 Db7 -}, &B1 ---}}
The 3 occurrences of tied "Ab1" and "B1" are shown in colour. "Ab1&" is the beginning of a tie and "&Ab1" is the end (of the same colour). Longer ties would occasionally require sequences such as "Ab1&" + "&Ab1&"+ "&Ab1".
These ties merge the (symbolic) time intervals of the beginning and ending occurrence. For example, the score "C4& &C4" could be replaced by "C4 _ " or equivalently "{2, C4}". The merging of time intervals is done in the FillPhaseDiagram() procedure of file "FillPhaseDiagram.c".
While parsing the compact polymetric structure to build the phase table — see Complex ratios in polymetric expressions — the algorithm calls GetSymbolicDuration() (in "SetObjectFeatures.c") to calculate the symbolic duration of a sound-object or simple note. By default, this is easy to calculate. The ignoreconcat flag is set to true if the sound-object or note is not followed by a '&'. The duration is set by prodtempo = Prod / tempo.
If ignoreconcat is false, GetSymbolicDuration() looks for the next acceptable occurrence of the note or sound object preceded by a '&'. Acceptability implies the following conditions:
- The note or sound-object should be on the same MIDI channel or the same Csound instrument;
- The date of the next occurrence should be later than the on-set date.
The conditions are readily apparent in the example. For example, "A1b&" cannot be paired with "&A1b" because the latter occurs at an earlier date. The next valid occurrence is "&A1b". The same applies to pairs shown in other colours. Each colour indicates a matching pair.
Once the duration has been set, the algorithm calls PutZeros() to fill as many columns as necessary to set the total duration of the pair of tied notes — as detailed in the page on Complex ratios in polymetric expressions.
In addition, when "&A1b" is parsed later, it should be ignored because the duration of the note has already been set by calling GetSymbolicDuration() and PutZeros() at the time of parsing "A1b&". Skipping these procedures is ensured by the foundendconcatenation flag.
Graphic display
The following is a sound-object graph of measures #20 to #21 on which the bounderies of intervals in tied notes are marked with dashed lines. The bounds of "Ab1& … &AB1" (red colour) are self-explanatory when compared with the musical score shown above: each occurrence is an instance of "{1/8, Ab1&} &Ab1".
Symbolic durations can be checked against physical time: since the tempo is 13/10, the first part has a physical duration of 1/8 x 10 / 13 = 0.09 seconds and the second part 10/13 = 0.77 seconds.
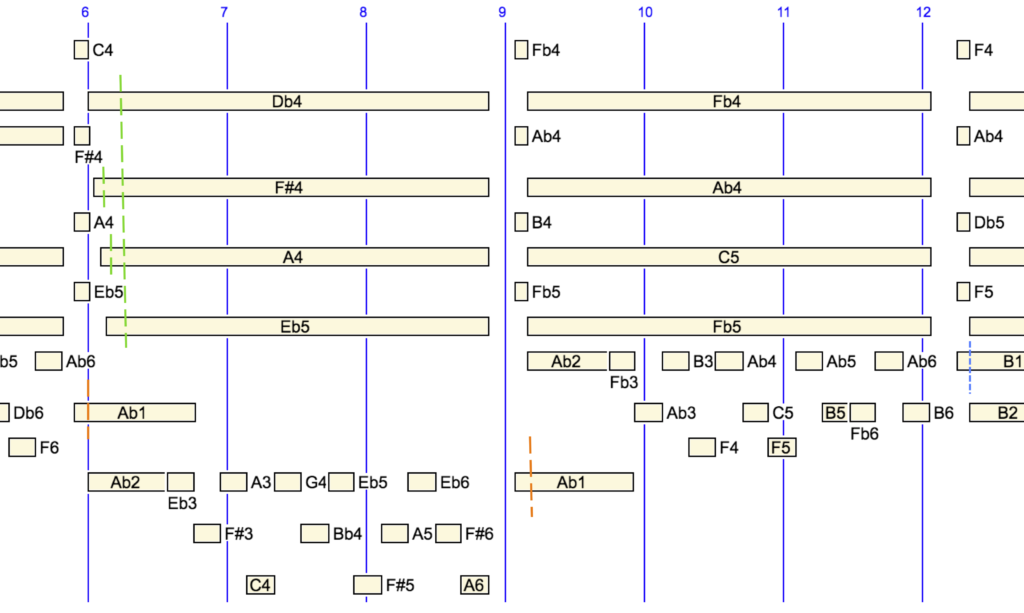
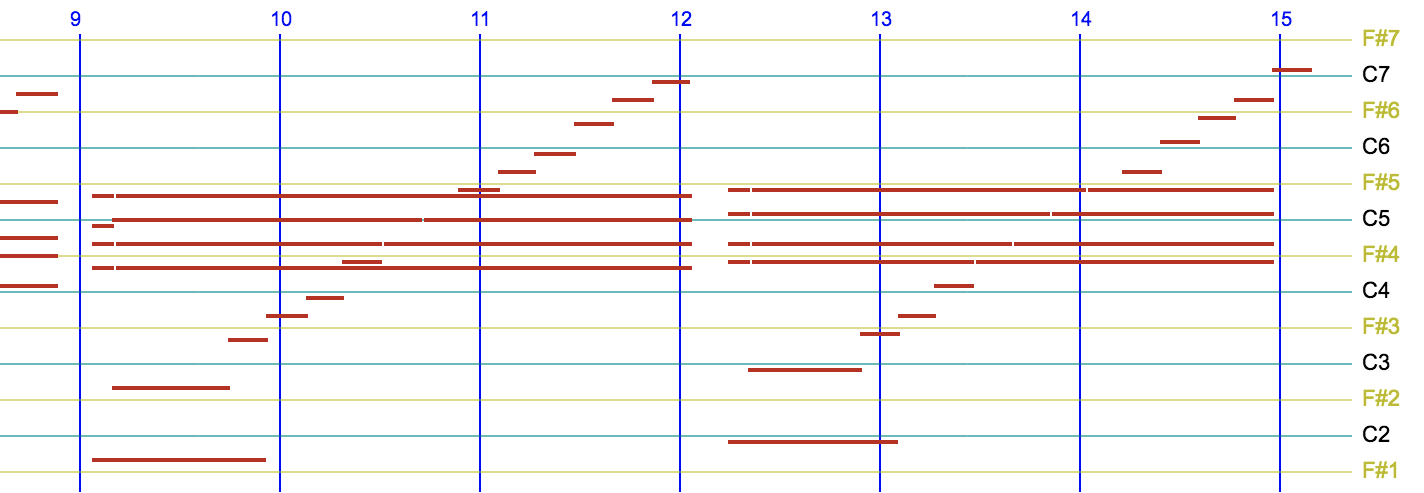
At the end of measure #21 the beginning of the note "B1&" is linked to its occurrence "&B1" in measure #22. The boundary is marked by a dashed blue line. The piano roll of measures #21-22 shows this connection of "B1":
Source: ManWithNoName in the MuseScore community
Arpeggios
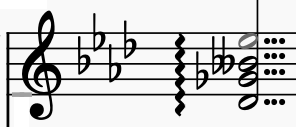
"{Db, Gb, Bbb, Eb}"
"Bbb" is interpreted as "A".
The green dashed lines belong to the polymetric expression {1/4,Db4& Gb4& A4& Eb5&}{7/2,&Db4,&Gb4,&A4,&Eb5}, the interpretation of an arpeggio on the chord at the beginning of measure #20. This interpretation is constructed when importing MusicXML files — see the PHP code in the file "_musicxml.php".
A short sequence "Db4 Gb4 A4 Eb5" (duration 1/4 beat) is played before the chord "{Db4, Gb4, A4, Eb5}" whose duration is set to 7/2 beats. Each note in the sequence is tied to its occurrence in the chord.
A sound example of an arpeggio can be found on the Importing MusicXML scores page.
More tied notes
A clear illustration of the use of tied notes and undetermined rests is a short musical phrase borrowed from a tutorial by Charles Ames, a pioneering designer of composition algorithms. The phrase is supplied as a musical score but its interpretation requires a careful analysis of the musical structure, resulting in the following Bol Processor score:
{{2,-{2,F#3}, -- {1,F5,A5}}{4,{ 1/2 ,G#3,E5,G5}{ 7/2 ,Bb4}}, _rest { 1/4 ,G#5&,C6,E6,B6&}{2,&G#5,&B6}}
To make things clear we need to look at the score in common music notation, divide it into blocks associated with variables, and finally write a grammar "-gr.Ames" to build the structure. Below are details of the analysis process and the resulting graphs of sound-objects and piano roll:

In this grammar, an undetermined rest has been written as "…". In its current version, the Bol Processor console no longer recognises the Unicode symbol for ellipsis "…". Therefore, it is automatically converted it to "_rest" by the PHP interface.
Undetermined rests are a powerful feature of polymetric expressions used to avoid tedious calculations. The polymetric expansion algorithm computes (symbolic) durations that produce the least complex expression. Read more in the Polymetric Structures tutorial.
The result of this computation is:
{{2,-{2,F#3}, -- {1,F5,A5}}{4,{ 1/2 ,G#3,E5,G5}{ 7/2 ,Bb4}}, 3 3/4 { 1/4 ,G#5&,C6,E6,B6&}{2,&G#5,&B6}}
Tied notes are exactly the ones indicated by links on the musical score. The sound rendering is:
Error tracing
The construction of suitable time intervals for tied notes depends on the matching of pairs — e.g. "A4&" followed by "&A4" — in the Bol Processor score. Some pairs may remain incomplete for one reason or another:
- The musical item has been split into chunks, using the PLAY safe (instead of PLAY) option to speed up computation, and the two parts belong to separate chunks;
- An error in the imported MusicXML score;
- An error in the algorithm — increasingly rare.
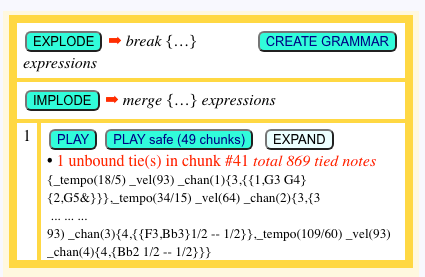
Case (1) is limited by the method for chunking items: each chunk is designed to contain the same number of start and end ties. However, this is not guaranteed because the chunks are limited in size.
Failure to balance ties is indicated below the PLAY safe button (see image).
Errors are shown in colour on the track being played.. These may not cause any noticeable changes in performance. However, we recommend that you report any incorrect data to the designers.
Below is an example of an error in a MusicXML score of Beethoven's Fugue in B flat major. A tie starts at note "Db5" (MIDI key #73) at the beginning of measure #573 (part 2), but it ends nowhere:

Read the MusicXML score fragment to check for this inconsistency. There are other inconsistencies in this score, such as a slur starting on note 'C4' of measure #646 (part 3) that does not end. This makes it difficult to interpret the slurs as legato.