Produce all items

 
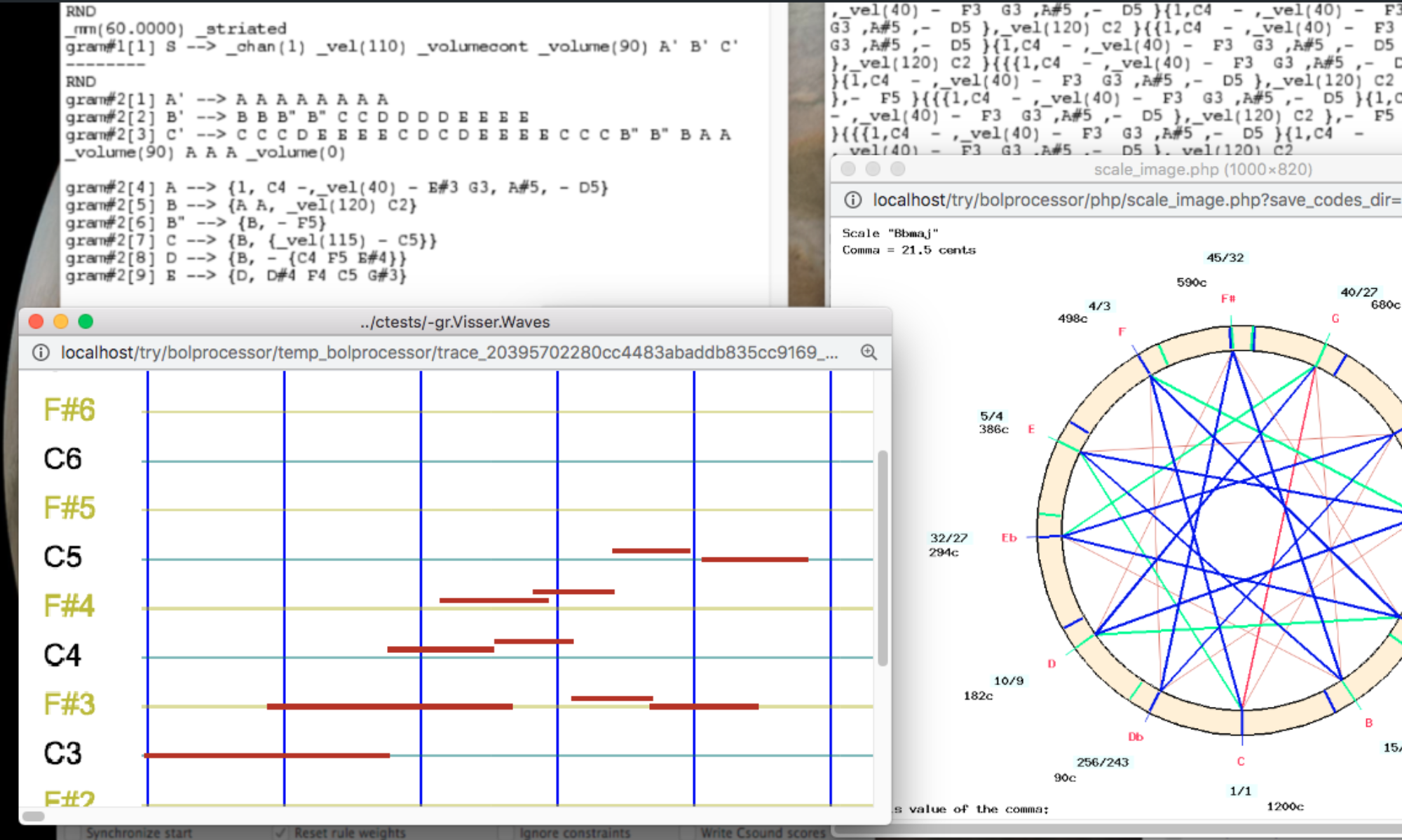
The core of the Bol Processor, in all its ver­sions, is an infer­ence engine capa­ble of gen­er­at­ing  'items'  — strings of vari­ables and ter­mi­nal sym­bols — treat­ed like the score of a musi­cal work. The infer­ence engine does this through the use of rules from a for­mal grammar.

In its ini­tial ver­sions (BP1 and BP2), the infer­ence engine was also able to analyse a score — for exam­ple, a sequence of drum beats — to check its valid­i­ty against the cur­rent gram­mar. This fea­ture is not (yet) imple­ment­ed in BP3.

 

 

A brief presentation of grammars

The gram­mars used by the Bol proces­sor are sim­i­lar to those described in for­mal lan­guage the­o­ry with a com­pre­hen­sive layout:

• Rules can be context-sensitive, includ­ing with remote con­texts on the left and the right.
• Rules can con­tain pat­terns of exact or pseu­do rep­e­ti­tions of frag­ments. Pseudo rep­e­ti­tions make use of trans­for­ma­tions (homo­mor­phisms) on the ter­mi­nal symbols.
• A ter­mi­nal sym­bol rep­re­sents a time object which can be instan­ti­at­ed as a sim­ple note or a sound object, i.e. a sequence of sim­ple actions (MIDI mes­sages or Csound score lines).
• The gram­mars are lay­ered — we call them 'trans­for­ma­tion­al'. The infer­ence engine first does every­thing it can with the first gram­mar, then jumps to the sec­ond, and so on.

The “produce all items” procedure

Grammars can pro­duce infi­nite strings of sym­bols if they con­tain recur­sive rules. This is of no prac­ti­cal use in the  Bol Processor, as it will even­tu­al­ly lead to a mem­o­ry over­flow. When recur­sive rules are used, con­trol is exer­cised by dynam­i­cal­ly decreas­ing rule weights or using  'flags'  to inval­i­date recursivity.

This means that the machine only gen­er­ates finite lan­guages with­in its tech­ni­cal lim­i­ta­tions. Theoretically, it should be able to enu­mer­ate all pro­duc­tions. This is the aim of the "pro­duce all items" pro­ce­dure. In addi­tion, iden­ti­cal items are not repeat­ed; to this effect, each new item is com­pared with the pre­ced­ing ones.

For geeks: This is done by stor­ing pro­duc­tions in a text file which is scanned for rep­e­ti­tions. The effi­cien­cy of this method depends on the tech­nol­o­gy of the work­ing disk. A SSD is high­ly recommended!

A simple example

Let us start with a very sim­ple gram­mar "-gr.tryAllItems0" which is made up of two lay­ers of subgrammars:

-se.tryAllItems0
-al.abc
RND
gram#1[1] S --> X X X
gram#1[2] S --> X X
-----
RND
gram#2[1] X --> a
gram#2[2] X --> b

The RND instruc­tion indi­cates that the rules in the gram­mar will be select­ed ran­dom­ly until no rule applies. The first sub­gram­mar pro­duces either "X X X" or "X X", then the machine jumps to the sec­ond sub­gram­mar to replace each 'X' with either 'a' or 'b'.

In the " Produce all items" mode, rules are called in sequence, and their deriva­tions are per­formed by pick­ing up the left­most occur­rence of the left argu­ment in the work string.

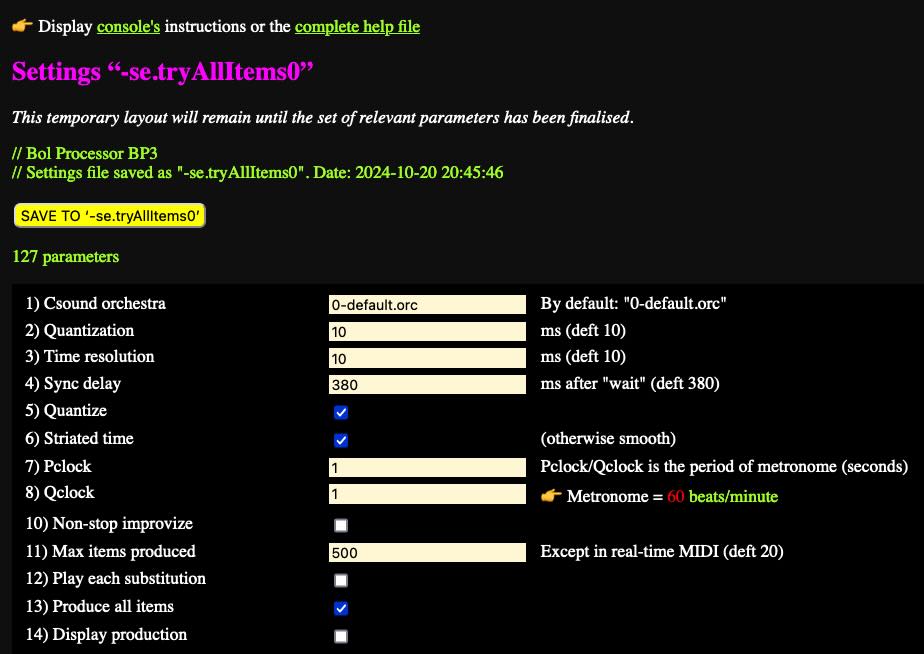
In the set­tings of " tryAllItems0 " (see pic­ture), "Produce all items" is checked. A para­me­ter " Max items pro­duced" can be used to lim­it the num­ber of productions.

The out­put is set to "BP data file" for this demo, although real-time MIDI, MIDI files and Csound score are pos­si­ble because 'a' and 'b' are defined as sound-objects. However, the sound out­put is com­plete­ly irrel­e­vant with this sim­ple grammar.

Any pro­duc­tion that still con­tains a vari­able is dis­card­ed. This nev­er hap­pens with the " tryAllItems0 " grammar.

The pro­duc­tion of this gram­mar is:

a a a
a a b
a b a
a b b
b a a
b a b
b b a
b b b
a a
a b
b a
b b

All the steps are shown on the self-explanatory trace:

Show the trace

A pattern grammar

Let us mod­i­fy "-gr.tryAllItems0" as follows:

-se.tryAllItems0
-al.abc
RND
gram#1[1] S --> (= X) X (: X)
gram#1[2] S --> X X
-----
RND
gram#2[1] X --> a
gram#2[2] X --> b

The first rule gram#1[1] con­tains a pat­tern of exact rep­e­ti­tion: the third 'X' should remain iden­ti­cal to the first one. Keeping the pat­tern brack­ets, the pro­duc­tion would be:

(= a) a (: a)
(= a) b (: a)
(= b) a (: b)
(= b) b (: b)
a a
a b
b a
b b

This out­put shows that the third ter­mi­nal sym­bol is a copy of the first. These items can be played on MIDI or Csound, as the machine will remove struc­tur­al mark­ers. However, struc­tur­al mark­ers can also be delet­ed on the dis­play by plac­ing a " _destru" instruc­tion under the "RND" of the sec­ond sub­gram­mar. This yields

a a a
a b a
b a b
b b b
a a
a b
b a
b b

To become more famil­iar with pat­terns (includ­ing embed­ded forms), try "-gr.tryDESTRU" in the "ctests" fold­er.

A more complex example

Consider the fol­low­ing gram­mar "-gr.tryAllItems1" in the "ctests" fold­er:

RND
gram#1[1] S --> X Y /Flag = 2/ /Choice = 1/
-----
RND
gram#2[1] /Choice = 1/ /Flag - 1/ X --> C1 X
gram#2[2] /Choice = 2/ X --> C2 X _repeat(1)
gram#2[3] <100-50> /Choice = 3/ X --> C3 X
gram#2[4] X --> C4 _goto(3,1)
gram#2[5] Y --> D3
Gram#2[6] X --> T
-----
RND
gram#3[1] T --> C5 _failed(3,2)
gram#3[2] Y --> D6

This gram­mar uses a flag 'Choice' to select which of the rules 1, 2 or 3 will be used in sub­gram­mar #2. Just change its val­ue to try a dif­fer­ent option, as they pro­duce the same 'lan­guage'. Terminals are sim­ple notes in the English con­ven­tion: C1, C2, etc. 

The flag 'Flag' is set to 2 by the first rule. If 'Choice' is equal to 1, rule gram#2[1] is applied, and it can only be applied twice due to the decre­men­ta­tion. This ensures that the lan­guage will be finite.

Rule gram#2[4] con­tains a "_goto(3,1)" instruc­tion. Whenever it is fired, the infer­ence engine will leave sub­gram­mar #2 and jump to rule #1 of sub­gram­mar #3. If the rule is a can­di­date, it will be used and the engine will con­tin­ue to look for can­di­date rules in sub­gram­mar #3. If the gram#3[1] rule is not applic­a­ble, the engine will jump to rule #2 of sub­gram­mar #3, as instruct­ed by "_failed(3,2)". In fact, these _goto() and _failed() instruc­tion have no effect on the final pro­duc­tion, but they do mod­i­fy the trace.

If 'Choice' is equal to 2, the " _repeat(1)" instruc­tion will force the gram#2[2] rule to be applied two times. If 'Choice' is equal to 3, the rule gram#2[3] will be applied twice because it has an ini­tial weight of 100 which is reduced by 50 after each appli­ca­tion. When it reach­es zero, the rule is neutralised.

For all val­ues of 'Choice' the pro­duc­tion is:

C1 C1 C4 D6
C1 C1 C4 D3
C1 C1 C5 D3
C1 C1 C5 D6
C1 C4 D6
C1 C4 D3
C1 C5 D3
C1 C5 D6
C4 D6
C4 D3
C5 D3
C5 D6

Since you insist, here is the out­put played in real time on a Pianoteq instrument!

We hope for more con­vinc­ing musi­cal examples. 😀