This page is intended for developers of the Bol Processor BP3 (read installation). It is not a formal description of the algorithms carried by the console's C code, but rather an illustration of their management of musical processes, which may be useful for checking or extending algorithms.
All examples are contained in the file "-da.checkPoly" in the "ctests" folder in the distribution.
Syntax of silences
In the Bol Processor's data/grammar syntax, silences (rests in conventional musical terminology) are represented either by a hyphen '-' for a single unit duration, or by integer ratios to specify a more complex duration:
- "4" is a rest of 4 units duration
- "5/3" is a rest of (approximately) 1.666-unit duration
- "3 1/2" is a rest of 3.5 units duration
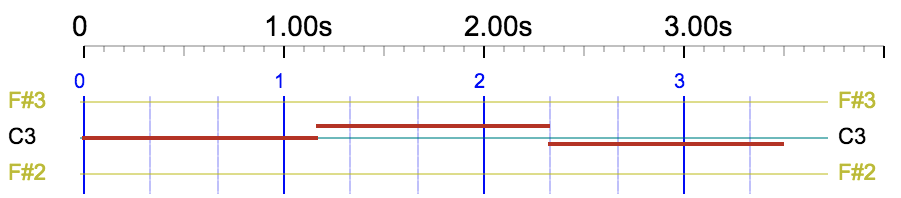
For example, "C4 C5 3/2 D5 E5" results in the following piano roll with a rest of 3/2 (1.5) units starting on beat 2 and ending on beat 3.5:

In this tutorial we will use the default metronome value = 60 beats per minute.
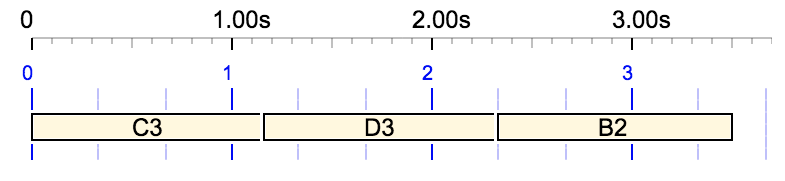
Another simple example is {3 1/2, C3 D3 B2}, which is the sequence of notes "C3 D3 B2" constrained to a total duration of 3 1/2 (3.5) beats. This silence is the first field of the polymetric expression (explained below). This results in the following piano roll:
or equivalently the sound-object graph:
Syntax of tempo
Any sequence of symbols conforming to the syntax of Bol Processor is processed as a polymetric expression. Typical forms are:
- field 1, field2 indicates that field1 and field2 should be superimposed and the total duration should be that of field1;
- field1.field2 indicates that field1 and field2 should be sequential, with the duration of each field being that of field1;
- {expression} is equivalent to expression.
Brackets '{' and '}' are used to create multi-level expressions.
A number of examples of polymetric expressions can be found in the Polymetric structures tutorial.
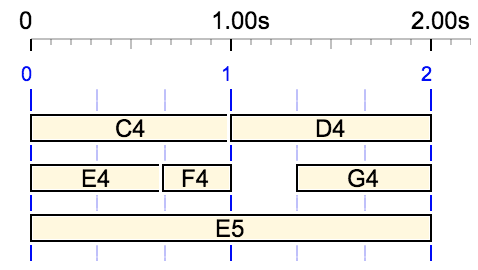
For example, {{C4 D4, E4 F4 G4}, E5} gives the following structure:
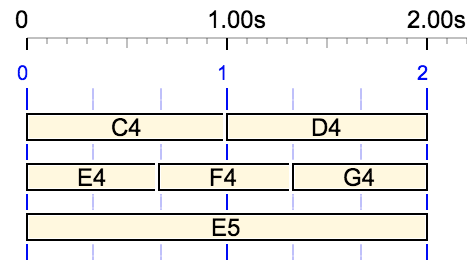
In order to interpret this structure, the Bol Processor needs to insert explicit tempo values into the expression. In fact, in this case, the most compact representation would be with explicit tempo values:
*1/1 {{C4 D4,*2/3 E4 F4 G4} ,*2/1 E5}
Expressions such as "*2/3" indicate that the duration of each note (or sound-object) should be multiplied by 2/3, regardless of the preceding statements. This means that the durations of notes "E4", "F4" and "G4" should be 2/3 seconds as shown in the diagram.
Creating the compact representation with its explicit tempo markers may require recursive calls of a sophisticated procedure called PolyExpand() in the "Polymetric.c" file.
At this stage it is important not to confuse the notations:
- "2/3" is a silence of duration 2/3 beats;
- "_tempo(2/3)" multiplies the current tempo by 2/3. This is a relative tempo marker;
- "*2/3" sets the current duration of the units to 2/3 of the metronome period. This is an absolute tempo marker. Similarly, "*4" multiplies durations by 4, and "*1/5" or "/5" divides them by 5 — whereas "1/5" is a 1/5 beat silence.
The third syntax is the one used by the Bol Processor's time-setting algorithms. Despite its syntactic validity, we do not recommend using it in grammars and data, as it can produce conflicting durations in polymetric structures. For example, {*2/1 A4 B4, *3/1 A5 B5} makes no sense because it tries to force the first field to have a duration of 2 x 2 = 4 beats and the second field to have a duration of 3 x 2 = 6 beats. The correct (never contradictory) way to change a tempo in data or grammars is to use the "_tempo(x)" performance tool.
Expanding a polymetric expression
In the previous paragraph we saw that {{C4 D4, E4 F4 G4}, E5} is internally represented as *1/1 {{C4 D4,*2/3 E4 F4 G4} ,*2/1 E5}. This internal representation is the most compact with explicit tempo markings. Therefore, it is the one that is maintained through all the steps of time setting.
Humans may prefer to see a more comprehensive representation called the expanded polymetric expression:
/3 {{C4_ _ D4_ _, E4_ F4_ G4_} , E5_ _ _ _ _}
This is done by clicking the EXPAND button on a data page. Underscores'_' represent extensions of the duration of the previous unit. These should not be confused with '-' (silence). To make things clearer, let us replace a '_' with a '-':
/3 {{C4_ _ D4_ _, E4_ F4 - G4_}, E5_ _ _ _ _}
This results in the following structure, where "F4" is not extended:
The expanded polymetric expression may become too large for a human observer. In this case only the compact version will be returned.
In the code of the Bol processor console, sound objects (of all kinds) are identified by numbers. The variable used to identify them in algorithms is always 'k' or 'kobj'. There is an option (in the code) to display object identifiers on a graph, which is set by the SHOWEVERYTHING constant. If set to true, this would be the previous sound object graph:
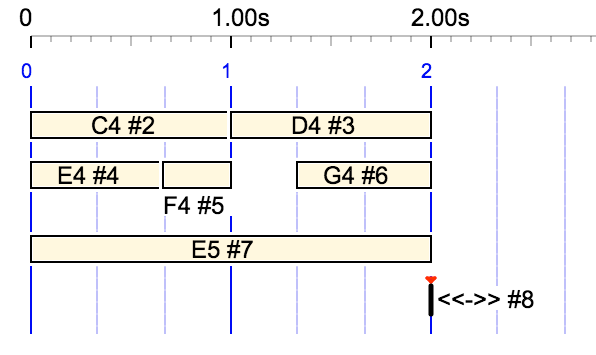
in SHOWEVERYTHING mode
Notes "C4", "D4", etc. have identifiers kobj = 2, 3, etc. The identifier "0" is reserved for extensions '_' and "1" for silences "-", none of which are shown in the graph. An exception is object #8, labelled <<->>, which is an out-time (zero duration) "silence" marking the end of the structure to facilitate its synchronisation with the next item.
The phase diagram
Given a compact polymetric structure, time-setting algorithms require a table in which each column is assigned a date (in physical time). The cells of this phase diagram contain the identifiers of the sound-objects, including "0" and "1". It is created by the procedure FillPhaseDiagram() in the file "FillPhaseDiagram.c".
It is easy to imagine that the table would become very large if no compression techniques were used. For example, Liszt's 14th Rhapsody would require no less than 9 x 1021 cells! The reason is that the Bol Processor calculates symbolic durations as integer ratios. A symbolic duration of 5/3 will never be replaced by "1.666" for two reasons: (1) roundings would accumulate as noticeable errors, and (2) we don't know in advance how many decimals we need to keep. The physical duration of 5/3 beats depends on the metronome and the sequence of "_tempo(x)" controls that change the tempo.
Let us first consider an unproblematic case. The polymetric expression /3 {{C4_ _ D4_ _, E4_ F4 - G4_}, E5_ _ _ _ _} creates the following phase diagram:
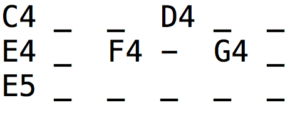
/3 {{C4_ _ D4_ _, E4_ F4 - G4_}, E5_ _ _ _ _}
In this example, if the metronome is set to 60 beats per minute, the physical duration assigned to each column is 1/3 second = 333 ms. As the graph becomes larger, this physical duration may decrease beyond the limit. This is where quantization comes in. It is set to 10 milliseconds by default, which means that two events occurring within 10 ms of each other can be written into the same column. To do this, the compact polymetric structure is rewritten with a compression rate (Kpress) that makes it fit into a phase diagram of suitable size.
If the piece of music lasts 10 minutes, we'll still get 10 x 60000 / 10 = 60000 columns in the table. Filling the phase diagram requires a very high compression rate, for example more than 5 x 1012 for Beethoven's Fugue in B-flat major.
To make matters worse, the algorithm has to deal with sequences of events that fall into the same column. This situation is signalled by the variable toofast, which is obtained by comparing the current tempo with the maximum tempo accepted in the structure. In the case of toofast, each event is written to a new row of the table in such a way as to respect the sequential order of the stream.
So we end up with 12132 lines for the phase table of Beethoven's fugue, in which the longest toofast stream contains 625 events — notes or sound-objects. These 625 events, which occur within a single frame of 10 ms, actually include '_' events which are extensions of notes belonging to the stream.
Dealing with complex ratios
In Bol Processor terminology, an integer ratio p/q is "complex" if either 'p' or 'q' exceeds a limit that depends on the source code. The limit is ULONG_MAX, the maximum value of an unsigned long type, currently 18446744073709551616.
In the code of the Bol Processor console, 'p' and 'q' are actually coded as double floating point numbers whose mantissa can contain as many digits as unsigned long integers. Arithmetic operations are performed on the fractions. Each resulting fraction is checked for complexity by a procedure called Simplify() in the "Arithmetic.c" file:
- While 'p' or 'q' is greater than ULONG_MAX, divide 'p' and 'q' by 10;
- Divide 'p' and 'q' by their greatest common divisor (GCD).
Part (1) of the Simplify() procedure generates rounding errors, but these represent a few units of very large numbers. In this way, the accuracy of symbolic durations is maintained throughout the computation of complicated polymetric structures.
Complex ratios in silences
Let us check the effect on quantization by playing:
C4 C5 36001/24000 D5 E5
The ratio 36001/24000 cannot be simplified. However, 1/24000 beat would take 0.04 ms which is much less than the 10 ms quantization. So, the ratio can be approximated to 36000/24000 and simplified to 3/2. The final result is therefore "C4 C5 3/2 D5 E5":

Let us now consider "C4 C5 35542/24783 D5 E5" which looks similar, as 35542/24783 (1.43) is close to 1.5. However, the calculation is more complex… Using the 10 ms quantization, the ratio is reduced to 143/100 and the compact polymetric expression is:
/1 C4 C5 /100 - _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ /1 D5 E5
The 143/100 silence is now represented as a single '-' (kobj = 1) followed by 142 '_' (kobj = 0). This sequence is toofast because tempomax, the maximum tempo accepted here, would be '50' instead of '100'. The compression rate is Kpress = 2. A full explanation requires the polymetric algorithm explained here.
The process of filling the phase table can be found in "FillPhaseDiagram.c". We call 'ip' the index of the column into which the next event is to be plotted. In the most common situation, e.g. writing "C4 _ _" (object #2), two procedures are called:
- Plot() writes '2' (kobj) into column ip
- PutZeros() writes two zeros into the columns ip + 1 and ip +2.
So, "C4 _ _" will have a symbolic duration of 3 units, as expected.
The case is different with a silence of 143/100, because the toofast situation requires that less than 142 '_' should be inserted after '-'. To this end, a (floating-point) variable part_of_ip is initialised to 0 and gets incremented by a certain value until it exceeds Kpress. Then Plot() and PutZeros() are called, part_of_ip is reset and a new cycle starts… until all 142 '_' of the compact polymetric expression have been read.
The increment of part_of_ip in each cycle is:
part_of_ip += Kpress * tempomax / tempo;
In this simple example, tempo = 100, tempomax = 50 and Kpress =2. So the increment is 1 and part_of_ip will reach the value of Kpress after 2 cycles. This means that every other '_' will be skipped.
Incrementing ip requires a more complicated process. The algorithm keeps track of the column numbers in the table as it would be created with Kpress = 1. These numbers are usually much larger than those of the actual phase diagram. The large number i is mapped to ip using the Class() function:
unsigned long Class(double i) {
unsigned long result;
if(Kpress < 2.) return((unsigned long)i);
result = 1L + ((unsigned long)(floor(i) / Kpress));
return(result);
}
So, each cycle of reading '_' in the toofast situation ends up incrementing i and then updating ip via the Class(i) function. The increment of i is:
prodtempo - 1
in which:
prodtempo = Prod / tempo
The variables Prod and Kpress are calculated after the compact polymetric expression has been created. Prod is the lowest common multiple (LCM) of all tempo values, i.e. '100' in this example.
Let us use the integers Pclock and Qclock to define the metronome value as Qclock * 60 / Pclock. If the metronome is set to its default value of 60 bpm, then Pclock = Qclock = 1.
The following (simplified) code calculates Kpress and updates Prod accordingly:
Kpress = 1. + (Quantization * Qclock * Prod) / Pclock / 1000.;
if(Kpress > 1.) {
s = LCM(Prod, Kpress) / Prod;
if(s > 1. && s < 10. && Prod < 1000000.) Prod = Round(s * Prod);
s = Round(Prod / Kpress);
if(s > 10.) Prod = Kpress * s;
}
As expected, we get the following sound-object graph:
The silence duration is 35542/24783 = 1.43 beats.
A more complex structure
This is a phrase from Liszt's 14th Hungarian Rhapsody:
_tempo(80/39) {F1, C2} {2, F2} 667/480 {53/480, G1, G2} {1/2, Ab1, Ab2} {1/2, B1, B2}
The compact polymetric expression — with a some redundant ratios removed — is:
*39/80 {F1, C2} {F2 _} *13/12800 - _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ *689/12800 {G1, G2} *39/160 {Ab1, Ab2} {B1, B2}
which gives the following sound-object graph:
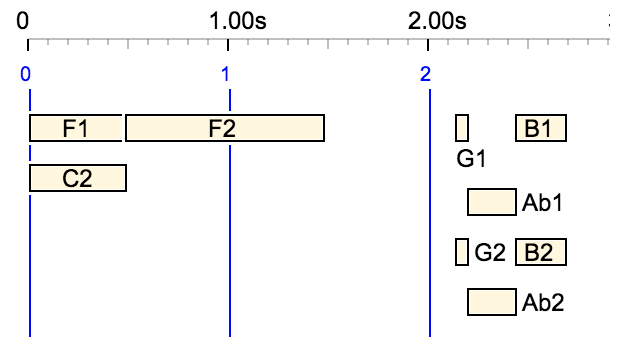
Metronome is set to 60 beats per minute.
Let us calculate the duration of the silence between "F2" and "G1" in two ways:
- In the source polymetric expression, this silence is notated as 667/480. Since the tempo is 80/39, its duration should be 667/480 * 39/80 = 0.67 beats (confirmed by the graph).
- In the compact polymetric expression, we find one '-' object followed by 666 '_' prolongations at a speed of *13/12800. The duration is therefore 667 * 13/12800 = 0.67 beats.
It would be difficult to follow the algorithm step by step because Prod = 2496100 , Kpress = 24961 and tempomax = Prod / Kpress = 100. Within the silence, tempo = 985 and the increment of part_of_ip is 24961 * 100 / 985 = 2 534.11167… The number of cycles before part_of_ip reaches the value of Kpress is ceil(9.85) = 10. This means that 9 out of 10 objects '_' have been skipped.
Conclusion
These examples and explanations provide insight into the code in the "FillPhaseDiagram.c" file of the console code. We hope that it will be useful for future development or migration of algorithms.
This is also a demonstration of the complexity of time calculations when dealing with polymetric structures capable of carrying all the details of real musical works — see Importing MusicXML scores for "real life" examples.