This page presents a theoretical framework for tuning musical scales, with a focus on just intonation and its application in various musical traditions, notably North Indian raga and Western harmonic music. It critiques traditional, mathematically driven approaches to intonation, advocating a practise-based understanding inspired by ancient Indian theories instead. The text also discusses how computer-controlled instruments can facilitate the implementation of microtonality, enabling the creation of scales that accommodate different concepts of consonance. Ultimately, the text proposes a unified approach to consonance that aims to bridge historical and cultural gaps in musical tuning.
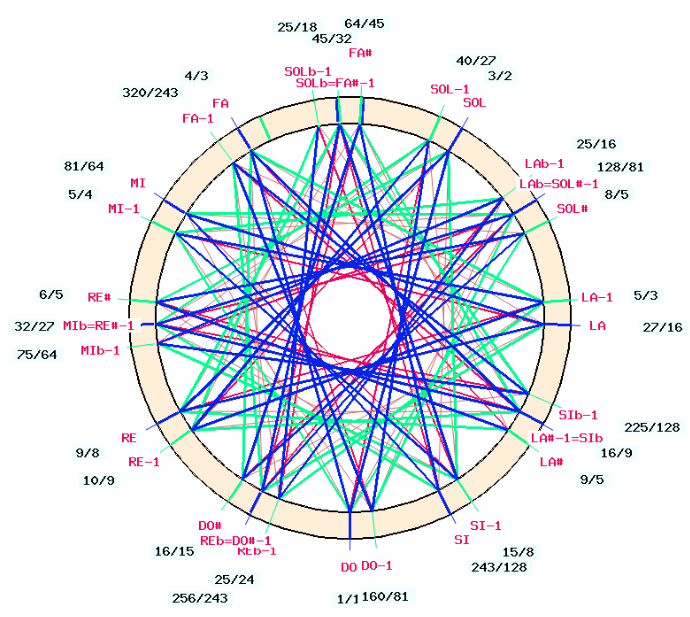
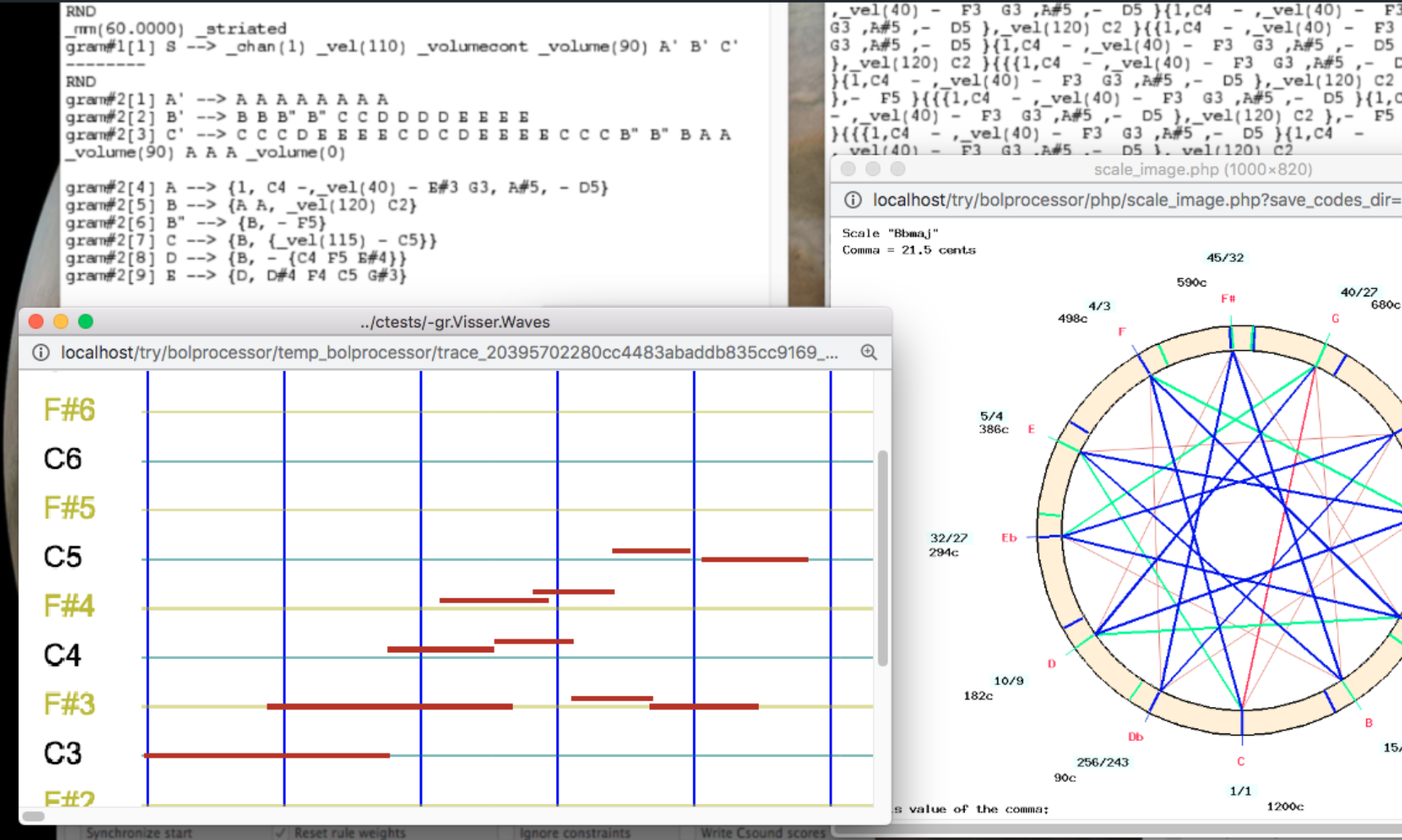
Image created by Bol Processor based on a model by Pierre-Yves Asselin
For more than twenty centuries, musicians, instrument makers and musicologists have devised scale models and tuning procedures to create tonal music that embodies the concept of "consonance".
This does not mean that every style of tonal music aims to achieve consonance. This concept is nonetheless explicit in the design and performance of North Indian raga and Western harmonic music. It is commonly believed that the octave and the major fifth (the interval from 'C' to 'G') form the basis of these models. Additionally, the harmonic major third (the interval from 'C' to 'E') has recently played an important role in European music.
Computer-controlled electronic instruments are opening up new avenues for the implementation of microtonality, including just intonation frameworks that divide the octave into more than 12 degrees - see the Microtonality page. For centuries, Indian art music claimed to adhere to a division of 22 intervals (the ṣruti-swara system) theorised in the Nāṭyaśāstra, a Sanskrit treatise dating from between 400 BCE and 200 CE. Since consonance (saṃvādī) is the basis of both ancient Indian and European tonal systems, we felt the need for a theoretical framework that encompassed both models.
Unfortunately, the subject of "just intonation" is presented in a wholly confusing and reductive manner (read Wikipedia), with musicologists focusing on integer ratios that presumably reflect the distribution of higher partials in periodic sounds. While these speculative models of intonation may support beliefs in the "magical" properties of natural numbers — as claimed by Pythagoreanists — they have rarely been tested against undirected musical practice. Instrument tuners rely on their own auditory perception of intervals rather than on numbers, despite the availability of "electronic tuners"…
Interestingly, the ancient Indian theory of natural scales did not rely on arithmetic. This may be surprising given that in Vedic times mathematicians/philosophers had laid out the foundations of calculus and infinitesimals which were much later exported from Kerala to Europe and borrowed/appropriated by European scholars — read C.K. Raju's Cultural Foundations of Mathematics: the nature of mathematical proof and the transmission of the calculus from India to Europe in the 16th c. CE. This epistemological paradox was an incentive to decipher the model presented by the author(s) of the Nāṭyaśāstra by means of a thought experiment: the two-vina experiment.
Earlier interpretations of this model, mimicking the Western habit of treating intervals as frequency ratios, failed to explain the intervalic structure of ragas in Hindustani classical music. In reality, the implicit model of the Nāṭyaśāstra is a 'flexible' one because the size of the major third (or equivalently the pramāņa ṣruti) is not predetermined. Read the page on Raga intonation and listen to the examples to understand the connection between the theory and practice of intonation in this context.
In Europe, the harmonic major third was finally accepted as a "heavenly interval" after the Council of Trent (1545-1563), ending the ban on polyphonic singing in religious gatherings. Major chords— such as {C, E, G} — are vital elements of Western harmony, and playing a major chord without unwanted beats requires the simplest frequency ratio (5/4) for the harmonic major third {C, E}.
With the development of fixed-pitch keyboard instruments, the search for consonant intervals gave way to the elaboration of theoretical models (and tuning procedures) that attempted to perform this interval in "pure intonation". Theoretically, this is not possible on a chromatic scale (12 degrees), but it can be worked out and applied to Western harmony if more degrees (29 to 41) are allowed. Nevertheless, the choice of enharmonic positions suitable for a harmonic context remains an uncertain proposition.
Once again, the Indian model comes to the rescue, because it can be extended to produce a consistent series of twelve "optimally consonant" chromatic scales, corresponding to chord intervals in Western harmony. Each scale contains 12 degrees, which is more than the notes of the chords to which it applies. Sound examples are provided to illustrate this process — see the Just intonation: a general framework page.
The tuning of mechanical keyboard instruments (church organ, harpsichord, pianoforte) to 12-degree scales made it necessary to distribute unwanted dissonances (the syntonic comma) over series of fifths and fourths in an acceptable manner. From the 16th to the 19th centuries, many tempered tuning systems were developed in response to the constraints of particular musical repertoires, with an emphasis on either "perfect fifths" or "pure major thirds".
These techniques have been extensively documented by the organist and instrument builder Pierre-Yves Asselin, along with methods for achieving intonation on a mechanical instrument such as the harpsichord. His book Musique et tempérament (Paris: Jobert, 2000, to be published in English) served as a guide for implementing a similar approach in the Bol Processor — see the pages Microtonality, Creation of just-intonation scales and Comparing temperaments. This framework should make it possible to listen to Baroque and classical works in the tunings intended by their composers, according to historical sources.
➡ Sadly, Pierre-Yves Asselin left this world on 4 December 2023. We hope that the English translation of his groundbreaking work will be completed soon.