The
time setting problem
Informally,
instanciating
a sound-objec
t
means dispatching to the sound processor all the messages that are defined in
its prototype.
A
naive interpretation of sequences of sound-objects would be to arrange all
corresponding time intervals in a strictly sequential way. Duthen and Stroppa
[1990] have suggested a more abstract approach, starting from the assumption
that any sound-object may possess one or several time points playing a
particular role, e.g. a climax. These points are called
time
pivots.
Further they suggest to construct sound structures using a set of
synchronisation rules. Their approach is attractive but it is difficult to
implement if the formalism of synchronisation rules remains too general.
Therefore we retained a simplified version of Stroppa's idea, assigning each
object one single pivot.
Let
us for instance consider a polymetric structure {S1,S2,S3} derived as
{a
_ b c d _ e , a _ f _ g h _ , j i _ a _ i _ }
yielding
the
phase
diagram:
|
a
|
_
|
b
|
c
|
d
|
_
|
e
|
NIL
|
|
a
|
_
|
f
|
_
|
g
|
h
|
_
|
NIL
|
|
j
|
i
|
_
|
a
|
_
|
i
|
_
|
NIL
|
The
definition of each object contains the relative location of its pivot and
metrical properties allowing the calculation of its dilation ratio (see
§3.1 supra).
Fig.15
is a graphic representation of a possible
instance
of this polymetric structure.
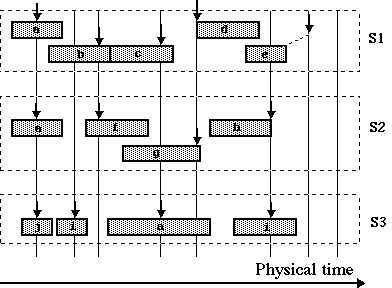 Fig.15
A structure of sound-objects
Fig.15
A structure of sound-objects
The
structure of tim
e
is for instance an irregular pulsation represented with the vertical lines (
time
streaks).
Objects 'c', 'f', "g" and 'a' have overlapping time-span intervals between the
third and fourth streaks.
Vertical
arrows indicate time pivo
ts.
As shown with object 'e', the pivot is not necessarily a time point within the
time-span interva
l
of the sound-object.
This
graphic represents the
default
positioning
of objects with their pivots located exactly on
time
streaks.
Although it is reasonable that instances of 'c', 'f' and 'a' are overlapping
between the third and fourth streaks since they belong to distinct sequences
which are performed simultaneously, it may not be acceptable that 'f' overlaps
'g' in a single sequence S2; the same with 'd' and 'e' in sequence S1. For
similar reasons, it may not be acceptable that the time-span intervals of 'j'
and 'i' are disjoint in sequence S3 while no silence is shown in the symbolic
representation.
How
could one deal with a constraint such as <<
the
end of sound-object 'f' may not overlap another sound-object in the same
sequence>>
?
If object 'g' is relocatable then it may be delayed (shifted to the right)
until the constraint is satisfied. We call this a
local
drift
of the object. However, the end of 'g' will now overlap the beginning of 'h'.
Assume that this also is not acceptable and 'h' is not relocatable. One should
therefore look for another solution, for example truncate the beginning of 'h'.
If this and other solutions are not acceptable then one may try to shift 'f' to
the left or to truncate its end. In the first case it might be necessary to
shift or truncate 'a' as well.
So
far we mentioned a constraint propagatio
n
within one single sequence. In the time setting algorith
m
the three sequences are considered in order S1, S2, S3. Suppose that the
default positioning of object
s
in S1 satisfies all constraints and no solution has been found to avoid the
overlapping of 'f' and 'g' in S2. Another option is to envisage a
global
drift
to the right of all objects following 'f' in S2. The global drift is notated
Δ on Fig.16. All time strea
ks
following the third one are delayed (see dotted vertical lines).
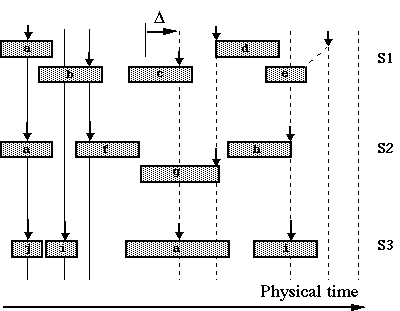 Fig.16
A structure using global drift
Fig.16
A structure using global driftThis
solution is labelled "
Break
tempo"
because its effect is similar to the the
organum
in conventional music notation. Although global drif
t
increases the delay between the third and fourth streaks, the
physical
duration
of sound objec
ts
is not modified because their dilation ratios have been calculated beforehand.
Now
the positioning of objects in S2 is acceptable but it might have become
unacceptable in S1: there may be a property of 'b' or 'c' saying that their
time-span intervals cannot be disjoint, so that 'c' could be shifted to the
left, etc. Evidently, whenever a global drift is decided the algorithm must
start again from the first sequence.
The
process of locating -- i.e. "instanciating" -- sound-objects, as illustrated in
this example, is the task of the
time
setting algorithm
imbedded in BP2.

