Polymetric
expressions
Polymetric
expressio
ns
are useful for string representations of
polyphonic
music.
A simple polymetric expressio
n
is shown figure 7 in staff notation, BP2 graphics and
phase
diagram
.
The latter is a table containing pointers to the instances of sound-objects
'C4', 'E#3', etc.
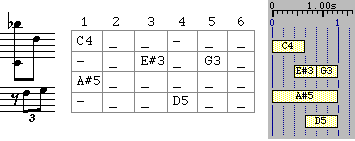
Fig.7:
Staff notation, phase diagram
and BP2 graphic display of a polymetric expression
notated "{1, C4 -, - E#3 G3, A#5, - D5}"
This
expression is notated "{1, C4 -, - E#3 G3, A#5, - D5}" on a BP2 text score.
It shows five sequences (
fields)
separated by commas. The leftmost field contains '1', the
symbolic
duration
of the expression. With a metronome set to 45 beats per minute, the resulting
physical duration is 1.33 seconds.
The
polymetric
expansion algorithm
imbedded in Bol Processor coerces all sequences of the structure to the same
symbolic duration. The second field contains a note 'C4' followed by a silence
'-', both of which will be treated as quavers. The third field contains the
sequence "- E#3 G3" which is performed as a triplet.
Thus,
the polymetric expressio
n
"{1, C4 -, - E#3 G3, A#5, - D5}" is expanded to "/6 {C4_ _ -_ _,-_ E#3_
G3_,A#5_ _ _ _ _,-_ _ D5_ _}" as suggested by the phase diagram. Symbol '_' is
a prolongation of the preceding sound-object, and '/6' indicates a change of
tempo after which durations are divided by 6.
The
phrase shown figure 7 is an excerpt of a musical example imitating Steve
Reich's style. A grammar generating examples in this style, composed by
Thierry Montaudon, is shown fig.8.
S
--> _velcont _vel(50) Part1 Part2 Part3
Part1
--> A A A A A A A A
Part2
--> B B B' B' C C D D D D E E E E
Part3
--> C C C D E E E E C D C D E E E E C C C B' B' B A A A A A
A
--> {1, C4 -,_vel(40) - E#3 G3, A#5, - D5}
B
--> {A A, _vel(60) C2}
B'
--> {B, - F5}
C
--> {B, _vel(55) - C5}
D
--> {B, - C4 F5 E#4}
E
--> {D, D#4 F4 C5 G#3}
Fig.8:
A grammar producing a piece
à
la
Steve Reich
In
this grammar, velocities are set by controls "_vel(x)" and are interpolated
throughout the piece due to instruction "_velcont". The upper four rules
define the deep structure of the piece. The lower ones use variables 'A', 'B',
'C'... to construct polymetric structures stringed together in each part of the
piece.
Consider
another example. Let {a b , c d e} be a sound structure in which two
sound-object sequences: "a b" and "c d e" are superimposed. The interpretation
chosen by BP2 is
{a
_ _ b _ _ , c _ d _ e _}
in
which '_' is a prolongation of the preceding sound-object. The two sequences
may be written on a two-line phase diagra
m
which
exclusively states that
'a' starts with 'c', 'd' starts before 'b' which in turn starts before 'e'...
The
interpretation of this polymetric expressio
n
automatically sets the tempo of "cde" at a speed which is 3/2 that of "ab".
This property may be used for indicating any fractional relative change of
tempo. For example,
/1
{4, a b c - - } {2, d e f} {5/3, g h}
indicates
that sequence "a b c - -" must be adjusted to fit exactly within 4 beats, then
"d e f" within 2 beats, then "g h" within 5/3 beats. BP2 performs the
necessary calculations and stretches the final representation. The fact that a
representation is ‘stretched’ does not mean it will be played
slower. BP2 calculates a time-scale factor to adjust its duration accordingly.
Integers,
fractions or hyphens indicating durations must appear in the
first
field of a polymetric expressio
n,
because if an expression contains no explicit tempo marker its default duration
is that of the first field. Compare for instance
/1
a b {c d, e f g} h i = /3 a _ _ b _ _ {c _ _ d _ _ , e _ f _ g _ } h _
_ i _ _
with:
/1
a b {e f g , c d} h i = /2 a _ b _ {e _ f _ g _ , c _ _ d _ _ } h _ i _
Another
feature useful for dealing with polymetric structures is the handling of
undetermined
rests:
notated '_rest' or '...' (Use option semi-colon on a US keyboard, never type
three periods) Each field in a polymetric expressio
n
may contain one undetermined rest appearing anywhere in the sequence. BP2
first determines the structure ignoring fields with undetermined rests, then it
scans again fields with undetermined rests. Some among them have fixed
durations because they contain an explicit tempo marker, e.g.:
{/1
fa5 {la5 si5,do6 re6 mi6}, do1 _rest /2 fa1 }
in
which the second field contains "/2", i.e. two sound-objects per time unit. It
also means that "do1" should be performed at (default)
one-sound-object-per-time-unit tempo, which is formally notated:
{/1
fa5 {la5 si5,do6 re6 mi6}, /1 do1 _rest /2 fa1 }
The
symbolic duration of the first field (hence, of the second field as well) is
that of sequence "/1 fa5 la5 si5", i.e. three units. The duration of the
second field is 3/2 units plus the undetermined rest. Therefore the
undetermined rest is also 3/2 units, which could have been written:
{/1
fa5 {la5 si5,do6 re6 mi6}, do1 3/2 /2 fa1 }
An
error message is generated if there is insufficient time for a rest. An
undetermined rest is meant to yield the
simplest
possible expression. For example,
{fa5 {la5 si5,do6 re6 mi6}, do1 re1 mi1 ... fa1 }
=
{fa5 {la5 si5,do6 re6 mi6}, do1 re1 mi1 - - fa1 }
=
{fa5 _ {la5 _ si5 _ , do6 _ re6 _ mi6 _ }, do1 re1 mi1 - - fa1 }
(See
Bel 1990a, 1991, 1992).
Let
us now compare polymetric expressio
ns
with
event
tables
used in MIDI sequencers. The following musical fragment is borrowed from the
COMPOSE
Tutorial and Cookbook
(Ames
1989:2):
 Fig.9
Fig.9
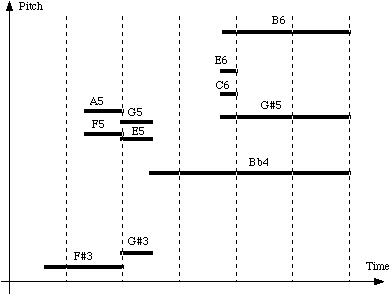 Fig.10
Fig.10The
list of events for this example is given in the
event
table
(ibid:3):
|
Period
.667
.667
.667
.5
1.25
0
2.25
|
Duration
.667
1.333
.667
.5
3.5
2.25
.25
|
Pitch
R
[rest]
F#3
F5:A5
G#3:E5:G5
Bb4
C6:E6
G#5:B6
|
where
"period" stands for the time elapsed from the on-setting of a note (or rest or
chord) to the on-setting of its successor.
A
possible (yet arguable) structural analysis of this example is
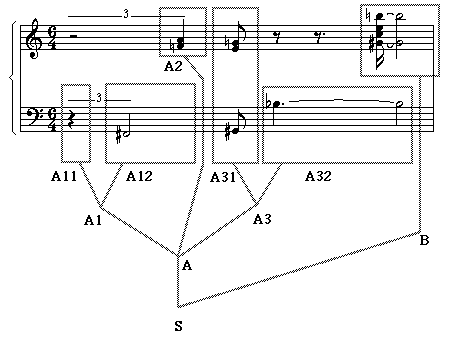 Fig.11
Fig.11The
score shown Fig.11 may be generated by the following grammar. Variables A1,
A2, etc. must be written between vertical bars so that they are not confused
with terminal symbols (musical notes A1, A2, etc.).
S
--> {|A|,... |B|}
A
--> {2, |A1|,2 |A2|} {4, |A3|}
|A1|
--> {|A11| ..., - |A12|}
|A3|
--> |A31| |A32|
|A11|
--> -
|A12|
--> {2,F#3}
|A2|
--> {F5,A5}
|A31|
--> {1/2,G#3,E5,G5}
|A32|
--> {3/2,Bb4&} {2,&Bb4}
B
--> {1/4,G#5&,C6,E6,B6&} {2,&G#5,&B6}
...
(other rules in the same grammar)
yielding
a unique derivation:
{{2
,{- ...,-{2 ,F#3}},2 {F5,A5}}{4 ,{1 /2 ,G#3,E5,G5}{3 /2 ,Bb4&}{2
,&Bb4}},...{1 /4 ,G#5&,C6,E6,B6&}{2 ,&G#5,&B6}}
Time
information is redundant in this representation (evidently, 4 = 1/2 + 3/2 + 2),
but it is consistent. BP2 will produce the following expanded representation
/12{{-_
_ _ _ _ _ _ F#3_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ,-_ _ _ _ _ _ _ -_ _ _ _ _ _ _
{F5_ _ _ _ _ _ _ ,A5_ _ _ _ _ _ _ }}{G#3_ _ _ _ _ ,E5_ _ _ _ _ ,G5_ _ _ _ _
}Bb4_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ & &Bb4_ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ ,-_ _ -_ _ -_ _ -_ _ -_ _ -_ _ -_ _ -_ _ -_ _ -_ _
-_ _ -_ _ -_ _ -_ _ -_ _ {G#5_ _ &,C6_ _ ,E6_ _ ,B6_ _ &}{&G#5_
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ,&B6_ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ }}
which
is internally represented:
/12
{/12 {/6 /18 - /9 F#3 /18 /6 ,/18 - -{/18 F5,/18 A5}/18 }/12 /12 {/24 G#3,/24
E5,/24 G5}/12 /8 Bb4&/12 /6 &Bb4 /12 /12 ,/12 /48 - - - - - - - - - - -
- - - - /12 {/48 G#5&,/48 C6,/48 E6,/48 B6&}/12 {/6 &G#5,/6
&B6}/12 }/12
The
philosophy behind polymetric representatio
n
is that it should contain a minimum amount of time information, for two major
reasons:
(1) there
is a lot of time information that the machine is able to calculate, for
instance here the duration of chord {F5, A5};
(2) timing
information should be based on final items, therefore on contextual information
regarding tempo.