6.
Time quantization
Phase
diagrams
(see for instance QuickStart §4.2) might have unwieldingly many columns
representing very short time delays (even less than the current time
resolution). Setting a
time
quantization
(an acceptable delay below which two events may be seen as simultaneous, i.e.
belong to the same column) helps BP2 to simplify phase diagra
ms.
In many cases this is compulsory for working with complex items in a limited
memory space.
The
following example demonstrates the quantization process. (Use "-da.tryQuantiz
e")
Consider the polymetric expressio
n
{do4
{re4 mi4, fa4 sol4 la4}, si4 do5}
which
is interpreted as:
{/6
do4{/6 re4 mi4, /9 fa4 sol4 la4}, /4 si4 do5}
with
the phase diagram (if quantization is OFF):
Metronome
setting mm = 60 produces the following item:
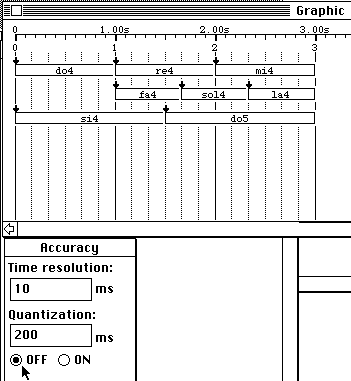 Fig.17
No time quantization
Fig.17
No time quantization
The
time delay between two consecutive time strea
ks
is 1000 / 6 = 166 milliseconds. This is also the delay between the off-setting
of "si4" and the on-setting of "sol4". Let us now use a quantization of 200 ms
forcing the interpreter to ignore shorter delays. The new item is shown Fig.18.
 Fig.18
Same item with 200 ms quantization
Fig.18
Same item with 200 ms quantizationThe
delay between the off-setting of "si4" and the on-setting of "sol4" is now
exactly 200 milliseconds, although it might have become 0 milliseconds in a
different context. This amounts to rewriting the item as:
/3{do4_
_ {re4_ _ mi4_ _ ,fa4_ sol4_ la4_},si4_ _ _ do5_ _ _ _}
with
the phase diagram:
Let
us take another example. The item shown Fig.14 of QuickStart:
b
b <<f>>{5 ,a c b,f - f}a <<chik>> b <<sync>>
was
assigned the phase diagram:
Here,
for instance, the symbolic duration of "b_ _ b_ _" is six time units. With a
mm = 400 metronome setting, the time delay between two time strea
ks
(i.e. two columns of the phase diagra
m)
was 50 milliseconds. If the quantization is set to 60 milliseconds, the phase
diagram becomes
which
yields the graphic score shown Fig.19.
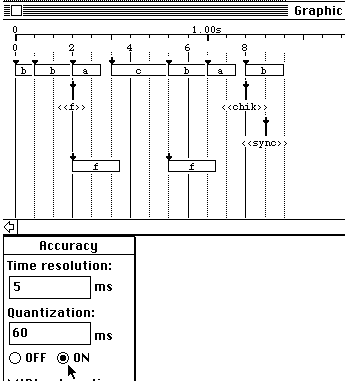 Fig.19
Item with 60 ms quantization
Fig.19
Item with 60 ms quantization
Durations
of the first two occurrences of 'b' have become unequal although the total
duration of "bb" remained two beats (i.e. 300 milliseconds). In this way, 'a',
'f' and "<<f>>" still have identical on-setting dates. Thus,
quantization simplifies the phase diagra
m
as much as possible while maintaining the dates of events within the given
range -- here, dates will match exact dates by ±60 milliseconds. In doing
so, durations may be adjusted within the acceptable range, but events that were
synchronised (on "vertical lines")
will
remain synchronised
.
Setting
quantizatio
n
to any value higher than 50 milliseconds yields the same result. Why? Since
the symbolic duration of the first occurrence of 'b' has become one time unit,
it cannot become smaller, otherwise sequentiality of the first two occurrences
of 'b' would be damaged.
The
quantization used by BP2 never affects sequentiality of sound-objects.
This is a very important feature because any pair of sound-objects may be used
to set a process on and off, e.g. NoteOn/NoteOff.
The
main advantage of BP2 quantization is an optimisation of computational spac
e
and time: it should be used systematically in projects where polymetric
structures are likely to yield oversized
phase
diagrams.
In effect, a quantization equal to the time resolution does not change final
timings although it is a safeguard against memory overflow.